
Matematika_Zaytsev_ch2
.pdf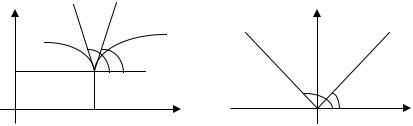
Приведённое выше определение производной функции y = f ( x ) обобщить, введя понятие односторонних производных – левой и правой.
Односторонние производные функции |
y = f ( x ) определяются так: |
||||
левая производная |
′ |
lim |
∆f |
|
, |
f ( x −0 ) = |
|
|
|||
|
∆x→0−0 ∆x |
|
|||
правая производная |
′ |
|
∆f |
. |
|
f ( x+0)= lim |
∆x |
|
|||
|
∆x→0+0 |
|
|
||
можно
(4)
(4/)
Очевидно, если функция имеет производную, то односторонние производные будут одинаковыми. Если же односторонние производные в некоторой точке x0
не равны, то в этой точке не существует производная f ′( x0 ) .
Односторонние производные функции будут равны угловым коэффициентам двух касательных (левой – 1 и правой – 2) в точке M ( x, y ) к кривой, являющейся
графиком |
функции y = f ( x ) |
′ |
=tgα1 |
и |
(рисунок 3), т.е. f ( x −0 )=k1 |
||||
′ |
=k2 =tgα2 . |
|
|
|
f ( x +0 ) |
|
|
|
Точка M, для которой tgα1 ≠ tgα2 , называется угловой точкой.
Y |
1 |
2 |
|
|
y=f(x) |
|
|
|
|
Y |
y=|x| |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y |
|
α1 α2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
M |
|
|
|
|
|
|
|
|
|
|
|
135˚ |
45˚ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
x |
|
|
|
X |
|
|
|
|
|
|
0 |
|
|
X |
|
|
Рисунок 3 |
|
|
|
|
|
|
Рисунок 4 |
||||||||
Пример 3. Для функции y = f ( x ) = |
|
x |
|
рассмотрим приращение при x = 0 : |
||||||||||||
|
|
|||||||||||||||
|
∆y = f ( 0 + ∆x ) − f ( 0 ) = f ( ∆x ) = |
|
∆x |
|
. |
|
||||||||||
|
|
|
|
|||||||||||||
Если ∆x > 0 , то∆y = ∆x и f ′( 0 + 0 ) = lim |
∆x = 1 . |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
∆x→+0 |
∆x |
−∆x |
|
|||
Если же ∆x < 0 , то ∆y = −∆x и f ′( 0 − 0 ) = |
lim |
= −1 . |
||||||||||||||
|
|
y = |
|
x |
|
x = 0 |
|
∆x→−0 |
|
∆x |
|
|||||
Итак, для функции |
|
при |
|
существуют различные односторонние |
||||||||||||
производные, |
поэтому |
при |
x = 0 |
эта функция |
не имеет производной. Точка |
|||||||||||
O( 0;0 ) будет угловой точкой. Заметим, что при x = 0 функция непрерывна. Полученные результаты иллюстрируются рисунком 4.
99
1.3 Непрерывность и дифференцируемость функции
Рассмотренный пример 3 показывает, что непрерывная функция может не иметь производной в некоторой точке. Однако из существования производной вытекает непрерывность функции.
Теорема 1. Если функция f ( x ) имеет в точке x производную, то эта функция непрерывна в этой точке.
Доказательство. По условию рассматриваемой теоремы существует конечный
предел lim |
∆ f = f ′( x ) . По теореме о связи между функцией и её пределом |
|||||
∆x→0 |
∆x |
|
|
|
||
|
∆ f |
|
′ |
( x ) +α , где α → 0 при ∆x → 0 . Отсюда можно выразить |
||
будем иметь |
∆x = f |
|||||
|
||||||
приращение функции |
|
|
|
|||
|
∆y = ∆ f ( x ) = ( f ′( x ) +α )∆x = f ′( x )∆x +α∆x . |
(5) |
||||
Следовательно, ∆ f ( x ) бесконечно малая величина при ∆x → 0 . Это и означает,
что функция непрерывна в точке x.
Таким образом, непрерывность функции в точке является необходимым условием существования производной функции в этой точке, но не достаточным!
Функция y = f ( x )называется дифференцируемой в точке x, если существует её конечная производная в этой точке. В этом случае верно равенство (5).
При этом, слагаемое f ′( x )∆x , линейное относительно ∆x, называется главной
частью приращения функции, так как другое слагаемое α∆x есть б.м. большего порядка, чем ∆x (почему?).
2. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Дифференцирование функции (отыскание производных) непосредственно на основе определения производной по формуле (1) оказывается практически неудобной процедурой. Нахождение производных значительно упрощается, если использовать общие правила дифференцирования, к рассмотрению которых мы переходим.
2.1 Производная постоянной, суммы, произведения и частного
1. Производная постоянной.
Рассмотрим функцию y = C , где C - постоянная величина. Запишем прираще-
ние этой функции ∆y = y( x + ∆x ) − y( x ) = C − C = 0 . |
|
||
Тогда y′ = lim |
∆y |
= 0 . Следовательно, |
|
∆x→0 |
∆x |
|
|
|
|
(C )′ = 0 , |
(6) |
т.е. производная постоянной величины равна нулю. 100
2. Производная суммы. |
|
и v = v( x ) имеют производные u′ , v′ |
|
|
|
||||||||||||||||||||||||
Пусть функции u = u( x ) |
|
в точке x. |
|||||||||||||||||||||||||||
Докажем, что функция |
y = u( x ) + v( x ) также имеет производную в той же точке |
||||||||||||||||||||||||||||
x и найдём её. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство. Придадим аргументу x приращение |
|
∆x , |
тогда |
|
|
функции |
|||||||||||||||||||||||
u , v и y получат, соответственно, приращения ∆u |
, ∆v и ∆y . Их новые зна- |
||||||||||||||||||||||||||||
чения |
|
u + ∆u , v + ∆v , y + ∆y |
|
|
связаны |
|
|
тем |
же |
|
соотношением: |
||||||||||||||||||
y + ∆y = ( u + ∆u ) + ( v + ∆v ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Отсюда |
|
∆y = ∆u + ∆v , |
∆y = |
|
∆u |
+ |
∆v |
, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
∆x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
∆x |
|
∆x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
′ |
|
∆y |
|
|
∆u |
|
|
∆v |
|
|
|
∆u |
|
|
∆v |
|
′ |
|
′ |
|
||||||||
y |
|
= lim |
|
= |
lim |
|
|
|
|
|
+ |
|
|
|
= |
lim |
|
|
|
+ lim |
|
|
= u + v |
|
. |
||||
|
∆x |
|
∆x |
∆x |
∆x |
|
|
|
|||||||||||||||||||||
|
|
∆x→0 |
|
∆x→0 |
|
|
|
|
|
∆x→0 |
∆x→0 ∆x |
|
|
|
|
|
|||||||||||||
Итак, |
|
|
|
|
|
y |
′ |
|
|
|
|
|
|
′ |
|
′ |
|
′ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
(7) |
|||||||
|
|
|
|
|
|
|
|
= ( u + v ) |
= u + v |
|
|
|
|
|
|
|
|
||||||||||||
т.е. производная суммы функций (имеющих производные) равна сумме производных этих функций.
Этот результат легко может быть распространён на любое число слагаемых,
так, например, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
′ |
|
|
′ |
+ w |
′ |
|
′ |
+ v |
′ |
+ w |
′ |
. |
||
( u + v + w ) = [( u + v ) + w] = ( u |
+ v ) |
|
= u |
|
|
||||||||||
3. Производная произведения. |
|
|
|
|
|
|
u = u( x ) , |
v = v( x ) , до- |
|||||||
При тех же предположениях относительно функций |
|
||||||||||||||
кажем, что функция y = u( x ) v( x ) имеет производную и найдём её. |
|
||||||||||||||
Доказательство. Приращение ∆x |
вызовет приращения |
∆u , |
∆v , ∆y соот- |
||||||||||||
ветственно у функций u , v и y = u v . При этом |
|
|
|
|
|
|
|
|
|
|
|
||||
y + ∆y = ( u + ∆u ) ( v + ∆v ) = uv + ∆u v + u ∆v + ∆u ∆v . |
|||||||||||||||
Отсюда ∆y = ∆u v + u ∆v + ∆u ∆v , |
∆y = |
|
∆u |
v + u |
∆v |
+ |
∆u |
∆v . |
|||||||
|
|
∆x |
∆x |
||||||||||||
|
∆x |
|
∆x |
|
|
|
|
|
|
|
|||||
Применяя теоремы о пределе суммы и произведения, будем иметь:
lim |
∆y = |
lim |
|
∆u |
v + u lim |
|
|
∆v |
|
+ lim |
∆u |
∆v . |
||||||||
|
|
|
|
∆x |
∆x |
|||||||||||||||
∆x→0 |
∆x |
∆x→0 |
∆x |
|
|
∆x→0 |
|
|
∆x→0 |
|
||||||||||
Учитывая, что lim |
∆u |
′ |
|
lim |
∆v |
= v |
′ |
, |
|
|
lim |
|
∆v = 0 (т.к. из дифференци- |
|||||||
|
|
|
|
|
|
|
|
|||||||||||||
∆x |
= u , |
∆x |
|
|
|
|
||||||||||||||
∆x→0 |
|
|
∆x→0 |
|
|
|
|
∆x→0 |
|
|
|
|||||||||
руемости функции v( x ) следует её непрерывность), получим: |
|
|||||||||||||||||||
|
|
|
|
y |
′ |
|
|
′ |
|
′ |
|
+ uv |
′ |
. |
|
(8) |
||||
|
|
|
|
|
= ( u v ) |
= u v |
|
|
||||||||||||
Формула дифференцирования произведения может быть обобщена на случай любого фиксированного числа сомножителей. Например,
101

(uvw)′=[(uv )w]′ =(uv )′w+(uv )w′=(u′v +uv′)w+uvw′= u′vw +uv′w +uvw′,
т.е. производная произведения функций (имеющих производные) равняется сумме произведений производной каждой из функций на все остальные функции.
Отсюда, в частности, получим ( Cu )′ = C′u + Cu′ = Cu′, т.к. (C )′ = 0 . Итак,
′ |
′ |
(9) |
( Cu ) |
= Cu , |
т.е. постоянный множитель можно выносить за знак производной.
4. Производная частного.
Если функции u = u( x ) , v = v( x ) удовлетворяют прежним предположениям и, кроме того, v( x ) ≠ 0 , то докажем, что функция y = u(v( xx )) также имеет произ-
водную и найдём её.
Доказательство. При тех же рассуждениях, что и выше, получим y +∆y = uv ++∆∆vu . Отсюда
|
u + ∆u |
|
u + ∆u |
|
u |
|
∆u v − u ∆v |
|
∆y |
|
∆u |
v − u |
∆v |
|
|
∆y = |
− y = |
− |
= |
, |
= |
∆x |
∆x |
. |
|||||||
v + ∆v |
v + ∆v |
v |
v( v + ∆v ) |
∆x |
v( v + ∆v ) |
||||||||||
|
|
|
|
|
|
|
|||||||||
Применяя теорему о пределах частного, суммы и произведения и учитывая непрерывность функции v(x) в точке x, убеждаемся в существовании производной
функции y = uv и получаем формулу :
|
|
′ |
|
′ |
′ |
|
|
u |
|
|
|
||||
|
u v − uv |
|
|
|
|||
y′ = |
|
|
= |
|
|
. |
(10) |
|
v2 |
|
|||||
v |
|
|
|
|
|||
Следовательно, производная частного или дроби (при условии, что числитель и знаменатель дроби имеют производные и знаменатель в нуль не обращается) равняется разности произведений производной числителя на её знаменатель и производной знаменателя на числитель, делённой на квадрат знаменателя.
2.2 Производная сложной функции
Пусть y = f(u), u = u(x), причём область значений второй функции входит в область определения первой. Тогда y является сложной функцией независимой переменной (аргумента) x, а u – промежуточной переменной: y = f(u(x)). Предположим, что функция u(x) имеет производную в точке x, а функция f(u), рассматриваемая как функция независимой переменной u, имеет производную в точке u, соответствующей точке x (т.е. между x и u должна быть связь u = u(x)). Докажем, что сложная функция y = f (u( x )) также будет иметь производную по x и най-
дём её.
102
Доказательство. Придадим x произвольное приращение ∆x. Пусть ∆u – соответствующее приращение функции u = u(x), а ∆y – приращение функции y = f(u), вызванное приращением ∆u. Воспользуемся соотношением (5), которое, заменяя x на u, запишем в виде:
∆y = fu / ∆u +α ∆u .
Здесь буквой «u» внизу отмечено, по какой переменной вычисляется производная. Величина α → 0 при ∆u → 0 . Разделив последнее равенство почленно на ∆x, получим
|
|
|
|
∆y |
|
|
/ |
|
|
∆u |
|
|
|
∆u |
|
|
|
|
|
|
|
|
|
= |
fu |
|
|
+α |
|
|
|
. |
|
|
|||
|
|
|
|
∆x |
∆x |
|
∆x |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если ∆x → 0 , |
то и |
∆u → 0 |
|
(т.к. функция u дифференцируема, а, значит, и |
||||||||||||||
непрерывна), а тогда и α → 0 . Следовательно, существует предел |
||||||||||||||||||
lim |
∆y |
= fu |
/ lim |
∆u |
+ lim |
|
α |
∆u |
= |
fu/ ux/ . |
||||||||
|
|
|
|
|
|
|
||||||||||||
∆x |
∆x |
|
||||||||||||||||
∆ x→0 |
|
|
∆ x→0 |
∆ x→0 |
|
|
|
∆x |
|
|
||||||||
Итак, |
|
|
|
yx/ |
= yu/ |
ux/ , |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
(11) |
||||||||
т.е. производная сложной функции по независимой переменной равна произведению производной этой функции по промежуточной переменной на производную промежуточной переменной по независимой.
Указанное правило было получено в случае одной промежуточной переменной. Однако это правило распространяется на случай сложных функций с большим числом промежуточных переменных. Так, например, при наличии двух промежуточных переменных u и v ( сложная функция имеет вид y = y( u( v( x ))) ) получим
yx/ = yu/ ux/ = yu/ ( uv/ vx/ ) = yu/ uv/ vx/ .
Отметим, что дифференцирование сложной функции занимает центральное место в технике дифференцирования, так как сложная функция (т.е. суперпозиция функций) – один из путей получения любой элементарной функции из простейших элементарных функций.
2.3 Производная обратной функции
Пусть у дифференцируемой функции y = f(x), f ′( x ) ≠ 0 существует обратная функция x = f −1 ( y ) . Докажем, что для обратной функции в соответствующей точке y : y = f ( x ) также существует производная и найдём её.
Доказательство. Придадим значению y произвольное приращение ∆y, тогда функция x = f −1 ( y ) получит соответствующее приращение ∆x. Заметим, что при ∆y ≠ 0 , ввиду однозначности самой функции y = f(x), будет и ∆x ≠ 0 . За-
103
пишем очевидное в этом случае равенство: |
∆x |
= |
1 |
. Если∆y → 0 , то будет |
|
∆y |
∆y |
||||
|
|
|
|||
|
|
|
∆x |
|
∆x → 0 (из дифференцируемости функции y = f(x) следует её непрерывность, а, значит, и непрерывность обратной функции x = f −1 ( y ) ). По определению производной получим
xy/ = lim |
∆x |
= lim |
1 |
= |
1 |
. |
|
|
∆y |
|
|||||
∆y→0 |
∆y |
∆x→0 |
|
yx/ |
|||
Итак, |
|
|
∆x |
|
|||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
xy/ = |
1 |
, |
|
|
(12) |
||
|
|
|
|||||
|
|
yx/ |
|
|
|
|
|
следовательно, производные прямой и обратной функции будут взаимно обратными величинами.
Y
M
0
Так как
|
|
Полученный результат можно полу- |
|
|
|
чить геометрически |
следующим обра- |
β |
y = f(x) |
зом. На рисунке 5 |
приведён график |
|
x = f −1(y) |
функции y = f ( x ). |
Но обратная функ- |
αция x = f −1 ( y ) имеет тот же график,
|
лишь независимая переменная для неё |
||
|
откладывается по оси OY . |
|
|
X |
Как |
следует из геометрического |
|
смысла |
производной |
функции, |
|
Рисунок 5 |
yx/ = tgα , xy/ = tgβ . |
|
|
|
|
α + β = 90° , то |
xy/ = tgβ = tg( 90° −α ) = ctgα = |
1 |
= |
1 |
. |
tgα |
|
||||
|
|
|
yx/ |
||
2.4 Производная функции, заданной в параметрической форме
Пусть дана система двух функций
x = f ( t ) |
. |
(*) |
|
|
|
||
y = g( t ) |
|
|
|
Предположим, что функция x = f ( t ) |
имеет обратную функцию t = f −1 ( x ) . |
||
Тогда переменная y, в силу соотношений |
y = g( t ) , |
t = f −1 ( x ) , будет сложной |
|
функцией от x: y = g( f −1 ( x )) = y( x ) . В этом случае система функций (*) опре-
деляет y как функцию от x, которую (напоминаем) называют функцией, заданной в параметрической форме (t – параметр).
104

Пусть функции |
x = f ( t ) и y = g( t ) дифференцируемы по t и xt / ≠ 0 . До- |
||||||||
кажем, что функция |
y = y( x ) имеет производную по x и найдём её. |
||||||||
Доказательство. В случае xt / ≠ 0 производная обратной функции t = f −1 ( x ) |
|||||||||
по x существует и определяется соотношением: tx/ = |
1 |
|
|
. По правилу дифферен- |
|||||
xt / |
|
||||||||
|
|
|
|
|
|
1 |
|
||
цирования сложной функции имеем yx/ |
= yt / tx/ = yt |
/ |
|
|
. Поэтому |
||||
|
|
|
|||||||
|
|
|
|
|
|
|
xt / |
||
|
yx/ = |
|
y / |
|
|
|
|
|
|
|
|
t |
. |
|
|
(13) |
|||
|
|
xt / |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Замечание. Полученная формула – зависимость yx/ |
от параметра t. Итак, если |
||||||||
функция была задана параметрически, то её производная тоже будет задана параметрически:
|
|
|
/ |
|
|
y / |
= |
yt |
|
||
xt / . |
|||||
|
x |
|
|||
x = x( t )
2.5 Дифференцирование функции, заданной неявно
Рассмотрим случай неявно заданной функции, т.е. когда функция y = y( x ) задаётся равенством вида F ( x , y ) = 0 . Если в это равенство подставить числовое
значение x и решить полученное уравнение относительно y, то при определённых условиях можно получить явное значение функции y = y( x ) . Например, равенст-
во 2 x − y + 1 = 0 определяет явно заданную функцию y = 2 x + 1 . Ясно, что не всегда удаётся однозначно выразить y из равенства F ( x , y ) = 0 . Так, например,
равенство |
x2 + y2 = 1 определяет две явно заданные функции y = 1 − x2 |
и |
|
1 |
|
y2 = − 1 − x2 . Во многих случаях бывает трудно аналитически (в виде формулы)
выразить явно y, а иногда и невозможно (например, в случае e y + xy2 = e ). Чтобы найти производную функции, заданной таким образом, нужно продиф-
ференцировать равенство F ( x, y ) = 0 по x, считая при этом величину y функцией
от x. При |
этом получим новое равенство, которое вместе с соотношением |
F ( x , y ) = 0 |
будет неявно определять производную y′( x ) . Поясним сказанное |
на примере. |
|
Пример |
4. Найти производную функции y = y( x ) , заданной равенством |
x2 + y2 = 1 ( y ≥ 0 ). Вычислить y′(0,5 ). 105
● Дифференцируем данное равенство по x, считая y функцией от x:
( x2 + y2 )x/ |
= (1)x/ . Так как ( x2 )x/ |
= 2 x , |
( y2 )x/ = ( y2 )/y yx/ = 2 y yx/ , |
(1)x/ =0 , |
|||||||||||
|
2 x + 2 y y |
′ |
= 0 |
y |
′ |
|
x |
|
|
|
что y |
′ |
|
x, и от y. |
|
то получим |
= − y . Видно, |
зависит и от |
|||||||||||||
|
|
|
|||||||||||||
Чтобы найти |
y′( 0 ,5 ) , нужно вначале определить |
y (0 ,5 ). Подставляя x = 0 ,5 в |
|||||||||||||
исходное равенство, получим 0 |
,52 + y2 (0 ,5) = 1 y (0 ,5) = 0 ,5 3 |
при усло- |
|||||||||||||
вии, что y ≥ 0 . Итак, y′(0 ,5 ) = − |
0 ,5 |
|
= − |
1 |
. ● |
|
|
|
|||||||
0 ,5 |
3 |
|
|
|
|
||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|||||
3. ПРОИЗВОДНЫЕ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Найдём производные степенной, показательной, логарифмической, тригонометрических и обратных тригонометрических функций.
1. Рассмотрим степенную функцию |
|
y = xa , где a – любое действительное чис- |
||||||||||||||||||||||||||||
ло. Предположим вначале, что x ≠ 0 . Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
∆x a |
− 1 |
||||
|
|
a |
|
a |
|
a |
|
|
∆x |
a |
|
|
|
|
∆y |
|
|
|
x |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
= x |
a |
|
|
|
|
; |
||||||||||||||
∆y = ( x + ∆x ) |
− x |
|
= x |
|
|
1 + |
|
|
|
|
|
− 1 |
, |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x |
|
∆x |
|
|
|
|
|
∆x |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x a |
− 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
∆y |
|
|
|
1 + |
x |
|
|
|
|
|
|
∆x |
a |
|
|
|
∆x |
|
|
|
|
|
|||||||
y′ = lim |
= xa |
lim |
|
|
|
|
|
|
|
|
= |
|
+ |
− 1 |
a |
|
при ∆x → 0 = |
|||||||||||||
∆x |
|
|
|
|
|
|
|
1 |
x |
|
|
x |
|
|||||||||||||||||
∆x→0 |
∆x→0 |
|
|
∆x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
∆x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
= xa |
lim |
|
|
|
x |
|
= axa−1 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Итак, |
|
|
|
|
|
|
|
∆x→0 ∆x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x |
a |
′ |
= ax |
a−1 |
. |
|
|
|
|
|
|
|
|
|
|
|
(14) |
||||||
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆y |
|
|
|
|
|
|
|
|
0, |
a >1 |
||
При x = 0 |
и a > 0 ∆y = |
|
|
a |
, |
|
|
′ |
|
lim |
= |
|
|
|
|
|
a−1 |
|
|
1, |
a =1 . |
|||||||||
( ∆x ) |
|
y = |
∆x |
lim ( ∆x ) |
= |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x→0 |
|
∆x→0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞, 0 <a <1 |
|||
Значение производной в первых двух случаях получается из (14) при x = 0 .
При x = 0 и a < 0 степенная функция разрывная и, следовательно, в этом случае производной не имеет.
106
Пример 5. Найти производные функций |
y = x , |
y = x2 , |
y = |
|
x , y = |
1 |
. |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
● Все перечисленные функции – степенные. Применим формулу (14): |
x |
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
′ |
1 ′ |
|
|
|
|
1−1 |
= x |
0 |
= 1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
( x ) = ( x ) = 1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
( x2 )′ = 2 x2−1 = 2 x , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
′ |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
( |
|
|
x )′ = x 2 |
= |
|
1 |
x 2 |
−1 |
= |
|
1 |
x−2 = |
|
1 |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2 |
|
|
2 |
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
′ |
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
= ( x−1 ) |
|
= −1 x−1−1 |
|
= −x−2 = − |
|
|
|
. ● |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. Найдём производную показательной функции |
|
y = a x (a > 0 , a ≠ 1). |
||||||||||||||||||||||||||||||||||||
Имеем ∆y = a x+∆x − a x = a x (a∆ x − 1) |
, |
∆y = a x |
a∆ x − 1 |
, |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆x |
|
|
|
|
|
∆x |
|
|
|
|
|
||||||||
y′ = |
lim |
∆y = a x lim |
a∆x − 1 |
= |
|
a∆x − 1 |
∆x lna при ∆x → 0 |
= |
||||||||||||||||||||||||||||||
|
∆x→0 |
∆x |
|
∆x→0 |
|
|
∆x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
= a x |
lim |
∆x lna |
= a x ln a. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
∆x→0 |
∆x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
(a x )′ = a x lna . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(15) |
||||||||||||||
В частности, |
(e x )′ = e x ( т.к. lne = 1) |
, (10 x )′ = 10 x ln10 и т.д. |
|
|
||||||||||||||||||||||||||||||||||
Пример 6. Найти производную функции y = 23 x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
● Данная функция сложная, поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
y′ = 23 x ln 2 (3 x )′ |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
3 |
x ln 2 |
|
|
|
|||||||||||||||
|
|
|
|
|
= 23 x ln 2 |
x− |
|
|
= |
|
. ● |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 3 x2 |
|
|
|||||
3. Рассмотрим логарифмическую функцию y = logax , x > 0 .
Используя правило дифференцирования обратной функции и формулу (15),
имеем x = a y , x y/ = a y ln a = x lna . По формуле (12) найдём yx/ = |
1 |
= |
1 |
. |
|
x y/ |
x lna |
||||
|
|
|
|||
Таким образом, |
|
|
|
|
|
107 |
|
|
|
|
|
|
|
|
|
|
(logax )′ = |
1 |
|
1 |
. |
|
|
|
(16) |
|
|
|
|
x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
ln a |
|
1 |
|
|
||
|
частности, при a = e для y = ln x |
|
имеем (ln x ) |
′ |
|
a = 10 |
||||||||
В |
|
= |
|
, а при |
||||||||||
|
x |
|||||||||||||
(lg x) |
′ |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
x |
ln10 |
|
|
|
|
|
|
|
|
||||
Пример 7. Вычислить производную функции y = ln x .
● Имеем |
|
|
|
|
|
|
|
|
ln x , x > 0 |
|
|
|
|
|
|
|
|
|
y = ln |
|
x |
|
= |
|
|
|
. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
ln( −x ) , x < |
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
′ |
|
1 |
|
|
|
|
′ |
|
1 |
′ |
1 |
|
|
||
Так как (ln x ) |
= |
|
и (ln( −x )) |
= |
|
( −x ) = |
|
|
|
(последнее равенство по- |
|||||
x |
−x |
|
x |
|
|||||||||||
лучено на основании дифференцирования сложной функции), то получим
(ln x )′ = 1x x ≠ 0 . ●
Замечание.
Отметим один приём, часто облегчающий дифференцирование. Это приём ло-
гарифмического дифференцирования, который состоит в следующем:
(ln f ( x ) )′ = f (1x ) f ′( x ) f ′( x ) = f ( x ) (ln f ( x ) )′,
т.е. производную функции можно представить в виде произведения самой функции и производной логарифма модуля функции. Полученное соотношение следует из рассмотренного примера 7 и правила дифференцирования сложной функции. Для упрощения записи условимся при логарифмическом дифференцировании знак модуля у f ( x ) опускать. Рассмотрим пример.
Пример 8. Найти производную функции f ( x ) = |
x10 |
x + 1 e x |
|
|
|
. |
|
|
2 |
||
|
( 2 x + 1 )( x + 2 ) |
||
● Так как функция представляет собою произведение пяти сомножителей, то находить производную этой функции трудно. Предварительно прологарифмируем эту функцию:
ln f ( x ) = 10 ln x + 0 ,5 ln( x + 1 ) + x − ln( 2 x + 1 ) − 2 ln( x + 2 ) .
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
f ′( x ) = |
10 |
+ |
|
1 |
|
+ 1 − |
|
1 |
|
2 − |
2 |
1 |
|
|
или |
||||||
|
f ( x ) |
|
x |
2( x + 1 ) |
2 x + 1 |
x + 2 |
|
|
||||||||||||||||
|
|
|
|
10 |
|
|
1 |
|
|
|
2 |
|
|
2 |
|
x |
10 |
x + 1 |
e |
x |
|
|||
f ′( x ) = |
+ |
|
|
|
+ 1 − |
− |
|
|
|
.● |
||||||||||||||
|
x |
2( x + 1 ) |
2 x + 1 |
x + 2 |
( 2 x + 1 )( x + 2 )2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
108 |
|
|
|
|
|
|
|
|
|
|
|
|
|
