Matematika_Zaytsev_ch2

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

f ( x ) − ( kx + b )

и cosα ≠ 0 .

Рисунок 14

.pdf

Скачиваний:

Добавлен:

14.02.2015

Размер:

2.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2315 16 17 18 19 20 21 22 23 > Следующая >>>

валы (см. рисунок 6).	Нетрудно исследовать знак

	f ′( x ),	вычислив	значение
	f ′( x ) в «удобных» контрольных
знак f /(x) «+»−1 «−» 0 «−» 1 «+» X	точках внутри каждого интервала.
	Итак, функция возрастает на
Рисунок 6	интервалах	( −∞,−1), ( 1,+∞)и

убывает на интервалах ( −1;0 ) и (0;1). •

2.2 Экстремум функции

Дадим вначале определение. Точка x0 называется точкой локального максимума (локального минимума) функции f(x), если существует такая окрестность U ( x0 )

точки x0, что	для любой точки x	из этой окрестности выполнено условие
f ( x0 ) ≥ f ( x )	( f ( x0 ) ≤ f ( x )) .	Слово «локальный» подчеркивает, что

f ( x0 ) является наибольшим (наименьшим) среди значений функции лишь в точ-

ках x, близких к x0. Очевидно, функция может иметь несколько локальных максимумов и минимумов, причём может оказаться, что иной локальный максимум окажется меньше какого–то локального минимума.

Y					На рисунке 7 изображён гра-
Y					фик функции y = f(x), у которой x1
					фик функции y = f(x), у которой x1
					и x3 – точки локального максиму-
					ма, x2 и x4 – точки локального ми-
					нимума. Минимум функции в точ-
					ке x4 больше её максимума в точке
					x1. Для обозначения локального
0	x1	x2	x3 x4	X	максимума или минимума исполь-
0	x1	x2	x3 x4	X	зуют объединяющий их термин –
		Рисунок 7			зуют объединяющий их термин –
		Рисунок 7			локальный экстремум. В дальней-

шем слово «локальный» будем опускать. Перейдём к вопросу о нахождении экстремумов функции.

Теорема 8 (необходимый признак существования экстремума).

Если функция f(x) имеет в точке x0 экстремум и в этой точке существует производная, то эта производная обращается в нуль, т.е. f ′( x0 ) = 0.

Доказательство. Пусть для определённости x0 – точка максимума. Тогда для всех малых по модулю ∆x справедливо неравенство f ( x0 )≥ f ( x0 +∆x ) или,

что то же, ∆ f = f ( x0 + ∆x ) − f ( x0 ) ≤ 0.

Тогда	∆ f	≤ 0 при ∆x > 0	и	∆ f	≥ 0 при ∆x < 0. Поэтому
Тогда	∆x	≤ 0 при ∆x > 0	и	∆x	≥ 0 при ∆x < 0. Поэтому
	∆x			∆x
					138

f ′( x0	+ 0 ) =	lim	∆ f	≤ 0 ,	f ′( x0	− 0 ) = lim	∆ f	≥ 0. Так как f ′( x0 )
	∆x→0+0		∆x			∆x→0−0	∆x
существует, то		f ′( x0 + 0 ) = f ′( x0 − 0 ), отсюда f ′( x0 ) = 0 , что и требовалось.

Геометрически это означает, что касательная к графику функции, проведённая в точке экстремума (если она существует), параллельна оси OX (см. рисунок 7).

Аналогичное доказательство для случая минимума советуем читателю провести самостоятельно.

Замечание. Теорема, обратная рассмотренной, неверна: необходимый признак экстремума не является достаточным. На-

Y			пример,	для функции	f ( x ) = x3 её про-
			изводная	f ′( x ) = 3 x2	обращается в нуль
			при x = 0, однако, точка x = 0 не является
			точкой экстремума (почему?).
			С другой стороны, точки, в которых
0	1	X	производная не существует, в этой теореме
	Рисунок 8		не рассматриваются. В таких точках воз-
			можен экстремум.

Например, на рисунке 7 в точке x3 функция имеет максимум, хотя её производная в этой точке не существует. Так функция y = x в точке x0 = 0 имеет минимум,

но не имеет производной при x0 = 0.

Разумеется, не всякая точка, в которой производная не существует, является точкой экстремума. Так, для функции f ( x ) = 3 x − 1 + 1 производная в точке x=1 не существует, а экстремума в этой точке нет (рисунок 8).

Итак, точками возможного экстремума (точками, подозрительными на экстремум) являются критические точки 1-го рода. Рассмотрим достаточные усло-

вия того, что критическая точка 1-го рода является точкой экстремума. Теорема 9 (1-й достаточный признак существования экстремума).

Пусть функция f(x) непрерывна в некоторой окрестности Uε ( x0 ) точки x0

и дифференцируема в каждой её точке, за исключением, быть может, точки x0. Если при переходе через точку x0 от меньших значений аргумента к большим («слева направо») производная меняет знак c «+» на «−», то x0 −точка максимума, если с «−» на «+», то x0 − точка минимума.

Доказательство.			Пусть	f ′( x ) при переходе через точку x0 меняет знак c «+»
на «−», т.е.		f ′( x ) > 0 при x0 − ε			< x < x0 и f ′( x ) < 0 при x0 < x < x0 + ε. То-
гда	по	формуле	Лагранжа		для	любой	точки x Uε ( x0 ) имеем
f ( x ) − f ( x0 ) = f ′( c )( x − x0 ), где с лежит между x и x0.
Если x ( x0 , x0 + ε ) ,				то f ′( c ) < 0 , x – x0 > 0, поэтому				f ( x ) − f ( x0 ) < 0.
Если	x ( x0 −ε , x0 ), то			f ′( c ) > 0,		x − x0 < 0,	поэтому	f ( x ) − f ( x0 ) < 0.
						139

Итак, x Uε ( x0 ) f ( x ) − f ( x0 ) < 0 ,	а	это означает, что точка x0 − точка
максимума.	f ′( x )c «−» на «+» рекомендуем чита-
Доказательство случая перемены знака
телю провести самостоятельно.		что если производная f ′( x ) не ме-
Из приведённого доказательства следует,

няет знака при переходе через точку x0, то в этой точке экстремума нет (так как не будет сохраняться знак разности f ( x ) − f ( x0 ) в окрестности этой точки).

Заметим, что если функция исследована на возрастание и убывание, то точки экстремума выделяются автоматически.

Пример 16. Исследовать на экстремум функцию f ( x ) = 2 x + 3 3 x2 .

• Функция определена и непрерывна при всех x. Производная

	′			2	−1	3		1 + 3	x	не существует в точке x1 = 0 и обращается в
f		( x ) = 2	+ 3 3 x				= 2 3 x

нуль, если 1 + 3 x = 0 , т.е. при x2 = − 1. Отметим эти точки на числовой оси и определим знак f ′( x ) на полученных интервалах (рисунок 9).

			Нетрудно убедиться, что
			lim f ′( x ) = ∞ (касательная
			x→0
			x→0
знак f /(x) «+» −1	«−»	0 «+» X	к графику функции в его
Рисунок 9			точке О(0; 0) вертикальна).
Рисунок 9
			Итак, точка x2 = − 1 −
точка максимума, максимум		f(−1) = 1; точка	x1 = 0 − точка минимума, мини-
мум f(0) = 0.

На рисунке 9 показаны также интервалы возрастания и убывания функции.

Рассмотрим достаточные условия экстремума, выраженные через производные высших порядков.

Теорема 10 (2-й достаточный признак существования экстремума).

Пусть в окрестности точки x0 функция f(x) непрерывно дифференцируема

(n+1) раз. Пусть	f ′( x0 ) = f ′′( x0 ) = ... = f ( n ) ( x0 ) = 0 , а				f ( n+1 ) ( x0 ) ≠ 0. То-
гда, если (n+1) −	нечётное число, то экстремума при x = x0				нет; если (n+1) −
чётное число, то экстремум		при x =		x0 есть, причём максимум, если
f ( n+1 ) ( x ) < 0 , и минимум, если		f ( n+1 ) ( x	0	) > 0.
0

Доказательство. Запишем формулу Тейлора n - го порядка в окрестности точки x0, учитывая, что первые n производных при x = x0 равны нулю:

140

f ( x ) = f ( x0 ) +		f ( n+1 ) ( c )	( x − x0 )n+1 .

		( n + 1 )!
Так как функция f ( n+1 ) ( x )	непрерывна в точке x0,			то существует некоторая
окрестность этой точки, в каждой точке которой знак				f ( n+1 ) ( x ) совпадает со
знаком f ( n+1 ) ( x ), т.е. f ( n+1 )	( x ) сохраняет знак. Пусть (n+1) − нечётное чис-
0

ло, тогда (x− x0)n+1 не сохраняет знак в окрестности точки x0 (при x < x0 он отри-

цателен,

при

он

положителен),

а,

значит,

f ( n+1 ) ( c )

( x − x )n+1 = f ( x ) −

f ( x

)

не сохраняет знак.

Это означает, что в

( n + 1 )!

точке x = x0

нет экстремума.

)n+1 > 0 x

Если (n+1)

−

чётное

число,

то

( x − x

знак

разности

f ( x ) − f ( x

)

совпадает со знаком f ( n+1 )( c ),

а, значит,

постоянный. Это оз-

начает, что при x = x0

экстремум есть. Кроме того, если f

( n+1 ) ( x ) > 0,

то и

f ( x ) − f ( x

) > 0

(x0

−

точка

минимума); если же

f ( n+1 ) ( x

) < 0,

то

f ( x ) − f ( x0

) < 0

(x0 −точка максимума), что и требовалось доказать.

Частный случай теоремы (n = 1). Если f(x) – дважды непрерывно дифферен-

цируемая функция в некоторой окрестности точки x0	и если f ′( x0 ) = 0 , а
f ′′( x0 ) ≠ 0, то x0 является точкой экстремума. При	f ′′( x0 ) < 0 точка x0 −

точка максимума, при f ′′( x0 ) > 0 точка x0 − точка минимума.

Пример 17. Исследовать на экстремум функцию f ( x )

= x4 − 2 x3 − 3x2

4 3 2

спомощью 2-го достаточного признака.

•Вычислим f ′( x ) и найдём критические точки 1-го рода:

f ′( x ) = x3 − 2 x2 − 3x, x3 − 2 x2 − 3x = 0, x( x2 − 2 x − 3 ) = 0 .

Полученное уравнение даёт три корня (три критические точки):

x1 = −1, x2 = 0 , x3 = 3. Вычислим f ′′( x ) = ( x3 − 2 x2 − 3x )′ = 3x2 − 4 x

Определим знак f ′′( x ) в каждой критической точке:

f ′′( −1 ) = 4 > 0, f ′′( 0 ) = −3 < 0, f ′′( 3 ) = 12 > 0. Следовательно, x1 = −

+ 5

−3.

1 −

точка минимума, f ( −1 ) =	53	− значение минимума; x2 = 0 − точка максимума,
точка минимума, f ( −1 ) =	12	− значение минимума; x2 = 0 − точка максимума,
	12			25
f(0) = 5 − значение максимума;		x3 = 3 − точка минимума,	f ( 3 ) = −	25	− значе-
f(0) = 5 − значение максимума;		x3 = 3 − точка минимума,	f ( 3 ) = −	4	− значе-
				4
		141

ние минимума. •

2.3 Выпуклость и вогнутость кривой. Точки перегиба

y=f(x)

f(x0)

График дифференцируемой функции y = f ( x ) называется выпуклым (выпук-

лым вверх) на интервале ( a,b ) , если

график на этом промежутке расположен ниже касательной, проведённой к графи-

ку этой	функции	в	любой точке
x ( a,b ) .	Если	же	на интервале
( a,b ) график функции			y = f ( x ) рас-

0 a	x0	b	X	полагается выше любой касательной,
	Рисунок 10			проведённой к графику этой функции, то
				его называют вогнутым (выпуклым вниз).
На рисунке 10 график функции			y = f ( x ) является вогнутым на интервале
( a, x0 ) и выпуклым на интервале ( x0 ,b ) .
Точка	( x0 , f ( x0 ))	графика функции		y = f ( x ) называется точкой перегиба,

если она разделяет выпуклую и вогнутую части графика.

Теорема 11 (необходимый и достаточный признак выпуклости и вогнутости).

Для функции f ( x ) , дважды непрерывно дифференцируемой на ( a,b ) , верно

утверждение: график функции

f ( x ) выпуклый (вогнутый)

на

( a,b ) тогда и

только тогда, когда f ′′( x ) ≤ 0

( f ′′( x ) ≥0)

x ( a,b ) .

Доказательство. Возьмём x0 ( a ,b ) ,

запишем формулу Тейлора для f ( x )

f ′( x0

)

f ′′( c )

при n = 1 :

f ( x ) = f ( x ) +

( x − x

) +

( x − x

) .

Уравнение касательной к графику функции

f ( x ) при x = x0 :

y = f ( x0 ) + f ′( x0 )( x − x0 ) .

Из этих двух равенств получаем:

f ( x ) − y =

f ′′( c )

( x − x )2 .

f ( x ) − y

f ′′( c ), поэтому

Отсюда видно, что знак разности

совпадает со знаком

f ( x ) ≤ y f ′′( x ) ≤ 0 , f ( x ) ≥ y f ′′( x ) ≥ 0 ,

x ( a,b ) ,

а это и требовалось доказать.

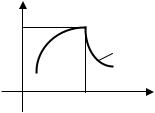
Теорема 12 (необходимый признак существования точки перегиба).

Пусть точка ( x0 , f ( x0 )) – точка перегиба графика дважды непрерывно

142

дифференцируемой функции f ( x ) , тогда f ′′( x0 ) = 0 .

143

Доказательство.		Допустим,	например,	что	при x < x0	график вогнут, т.е.
f ′′( x ) ≥ 0 , а при x > x0 – выпуклый, т.е.				f ′′( x ) ≤ 0 . Тогда, так как			f ′′( x ) по
условию непрерывная функция,			из условия	f ′′( x0 − 0 ) = f ′′( x0 + 0 ) = f ′′( x0 )
следует, что f ′′( x0 ) = 0 , что и требовалось доказать.
Y			Замечание. График функции может иметь
f(x0)			точку перегиба и при x = x0			таком, что
		y = f(x)	f ′′( x0 ) не существует (рисунок 11).

			Поэтому		возможными	точками	перегиба
			(«подозрительными на перегиб»)				являются
0	x0	X	точки, где вторая производная или равна нулю,
	Рисунок 11		или не существует. Такие точки называют кри-
			тическими точками 2-го рода. Заметим, что не
			всякая такая точка является точкой перегиба.

Например, для функций y = x3 и y = x4 вторые производные			y′′ = 6 x	и
y′′ = 12 x2 при	x = 0 обращаются в нуль.	При этом точка (0; 0) для графика
функции y = x3	является точкой перегиба,	а для графика функции	y = x4	не

является (советуем показать это, построив графики этих функций).

Выясним, в каком случае критическая точка 2-го рода будет точкой перегиба.

Теорема 13 (достаточный признак существования точки перегиба).

Пусть функция f ( x ) определена в окрестности критической точки 2-го рода

x = x0	и дважды непрерывно дифференцируема (хотя бы в проколотой окрест-
ности	точки	x0 ). Если	f ′′( x )	меняет знак при переходе через x0 , то
( x0 , f ( x0 ))		– точка перегиба.
Доказательство. Если			f ′′( x ) при переходе через		x = x0 сменила знак, то это
означает, что с одной стороны от x0				график функции	f ( x ) выпуклый, а с другой
вогнутый, т.е. при x = x0			произошёл перегиб графика.

Отсюда вытекает следующее правило отыскания интервалов выпуклости и вогнутости, а также точек перегиба графика функции y = f ( x ):

1)находим f ′′( x ) ;

2)находим точки, в которых f ′′( x ) равна нулю или не существует (критические точки 2-го рода);

3)определяем знак f ′′( x ) в каждом из промежутков, на которые область оп-

ределения функции разбивается найденными точками; 4) применяем достаточные признаки выпуклости и вогнутости, существования

точек перегиба, находим их координаты.

143

Пример 18. Исследовать на выпуклость и вогнутость, найти точки перегиба

графика функции f ( x ) = 2− \| x5 − 1 \| .
● Используя определение модуля, данную функцию можно записать в виде:
1 + x5		, x ≤ 1
f ( x ) =	− x5	.
3	− x5	, x > 1

Заметим, что функция непрерывна x R . Вычислим f ′( x ) = 5 x4								, x ≤ 1 .
							−5 x4	, x > 1

Производная f ′( 1 )		не существует, так как f ′( 1 − 0 ) = 5 ≠ f ′( 1 + 0 ) = −5 ,
поэтому f ′′( 1 ) также не существует.
При x ≠ 1 имеем	f ′′( x ) = 20 x3			, x ≤ 1 .
		−20 x3			, x > 1

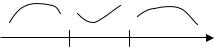
					Итак, критические точки 2-го рода:
					x1 = 0 (так как		f ′′( 0 ) = 0 ) и
					x2 = 1 (так как		f ′′( 1 )не существу-
Знак f //(x) «−» 0 «+»		1 «−»	X		ет). Отметим эти точки на числовой
Знак f //(x) «−» 0 «+»		1 «−»	X		оси (рисунок 12). В каждом из полу-
Рисунок 12					ченных интервалов определим
Рисунок 12					знак f ′′ . Например,
					знак f ′′ . Например,
f	′′			f	′′
f	(−1)=−20<0			f	( x)<0 x (−∞; 0);
f	′′				′′	>0 x ( 0;1 ) ;
f	( 0,5 ) = 2,5 > 0		f ( x )			>0 x ( 0;1 ) ;
f ′′( 2 ) = −160 f ′′( x ) < 0						x ( 1;+∞ ) .

Согласно теоремам 11 и 13 делаем вывод: на интервале ( −∞; 0 ) график выпуклый, на ( 0; 1 ) – вогнутый, на ( 1; +∞ ) – выпуклый. Для наглядности на участках выпуклости и вогнутости изображены соответствующие дуги. Точки

A( 0; 1 ) и B( 1; 2 ) – точки перегиба. Заметим, что точка В – угловая точка графика. ●

2.4 Асимптоты графика функции

При исследовании поведения функции на бесконечности, т.е. при x → ±∞ или вблизи точек разрыва 2-го рода, часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называют

асимптотами. Дадим строгое определение.
Прямая L : Ax + By + C = 0 называется	асимптотой графика функции
y = f ( x ), если расстояние d от точки M (x,	f ( x )) графика до этой прямой

L (измеряемое по перпендикуляру к L ) стремится к нулю при неограниченном удалении этой точки графика от начала координат.

144

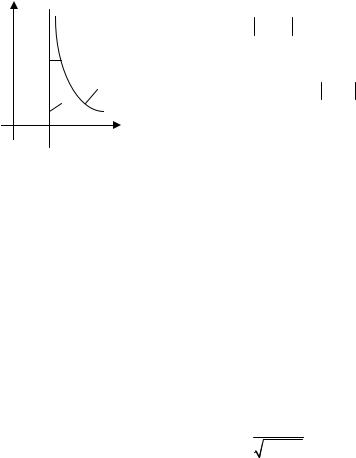
Итак, если у графика функции имеется асимптота, то график вдали от начала координат будет «похож» на прямую линию.

Обычно, отдельно рассматривают вертикальные асимптоты (случай B = 0 , тогда L : Ax + C = 0 или x = a – вертикальная прямая) и наклонные асимптоты (случай B ≠ 0 , тогда можно записать L : y = kx + b – наклонная прямая). Частный случай k = 0 будет соответствовать горизонтальной асимптоте.

Теорема 14 (необходимый и достаточный признак существования вертикальной асимптоты).

Прямая L : x = a является вертикальной асимптотой графика функции тогда и только тогда, когда выполняется хотя бы одно из соотношений:

lim f ( x ) = ±∞ ,	lim f ( x ) = ±∞ .
x→a+0	x→a−0

d M(x, f(x))

y = f(x)

x=a

Рисунок 13

Доказательство. Любое из четырёх указанных соотношений означает, что если x → a каким–либо

способом, то f ( x ) → ∞ , т.е. расстояние от точки

M (x, f ( x )) графика функции до начала координат неограниченно возрастает. Условие x → a означает, что расстояние d = x − a между точкой M и прямой L : x = a стремится к нулю. Всё это говорит

о том, что x = a – вертикальная асимптота.

На рисунке 13 показан случай, когда

lim f ( x ) = +∞ .

x→a+0

Замечание. Теорема 14 показывает, что наличие вертикальных асимптот у графика функции y = f ( x ) тесно связано с наличием точек разрыва 2-го рода у

функции f ( x ) .


Пример 19. Найти вертикальные асимптоты графика функции
f ( x ) =	x3		.
	2( x + 1 )2
● Данная функция имеет единственную точку				разрыва x1 = −1 (значение
f ( −1 ) не определено). Так как lim	x3			−1		x = −1
		=			= −∞ , то прямая

x→−1 2( x + 1 )2				+0

– единственная вертикальная асимптота. ●

Пример 20. Найти вертикальные асимптоты графика функции

f ( x ) = x . 1 − x2

145

● Данная функция определена и непрерывна на интервале ( −1; 1 ) , т.е. не име-

		−1				1
ет точек разрыва. Но lim	f ( x ) =		= −∞ ,	lim	f ( x ) =		= +∞ ,
ет точек разрыва. Но lim	f ( x ) =	+0	= −∞ ,	lim	f ( x ) =	+0	= +∞ ,
x→−1+0		+0		x→1−0		+0

поэтому прямая x = −1 является правосторонней вертикальной асимптотой (точки графика расположены только справа от этой асимптоты), а прямая x = 1 является левосторонней вертикальной асимптотой (точки графика расположены только слева от этой асимптоты). Отметим, что в примере 19 прямая x = −1 – двусторонняя вертикальная асимптота. ●

Займёмся нахождением наклонных асимптот, уравнения которых можно записать в виде y = kx + b .

Теорема 15 (необходимый и достаточный признак существования наклонной

асимптоты).
Прямая L : y = kx + b	является наклонной асимптотой графика функции
y = f ( x ) тогда и только тогда, когда существуют конечные пределы:
k = lim		f ( x )	,	b = lim ( f ( x ) − kx).	(14)

x→∞		x		x→∞

	Доказательство проведём только для случая
y= f(x) L	x → +∞ (случай	правосторонней наклонной
M(x, f(x))	асимптоты).		M
M(x, f(x))	Расстояние от	точки	M	графика функции
y= kx+b	y = f ( x ) до асимптоты		L	изображается отрез-
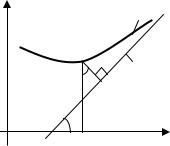
y= kx+b	ком MN (рисунок 14). Так как
N	ком MN (рисунок 14). Так как

PNMP = ( L,OX ) = α , то MN = MP cosα ,

αгде точка P( x; kx +b ) L . Имеем

Итак, L : y = kx + b – правосторонняя наклонная асимптота ( MN → 0

при x → +∞ ) ( MP →0 при x → +∞ )

( f ( x ) − kx ) .

lim

f ( x ) − kx −b

= 0 b =

lim

x→+∞

f ( x ) −kx

f ( x )

x→+∞

f ( x )

Так как lim

= lim

lim

−k =

0 , то k = lim

x→+∞ x

x→+∞

Если будут существовать соответствующие пределы при x → −∞ , то прямая L : y = kx + b будет левосторонней наклонной асимптотой. Если рассматриваемые пределы как при x → +∞ , так и при x → −∞ дадут одинаковые результаты

146

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 2315 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.20151.73 Mб316matem-up1.pdf
#
14.02.201554.78 Кб17Matematika-i-statistika-12-RiSO-B.doc
#
14.02.2015543.23 Кб30matematika_ekzamen - .doc
#
14.02.20152.69 Mб320matematika_metod_posobie.docx
#
14.02.20151.69 Mб232Matematika_ryad.doc
#
14.02.20152.17 Mб54Matematika_Zaytsev_ch2.pdf
#
14.02.20158.95 Mб92matematike_fepo_s_otvetami.doc
#
24.08.20193.22 Mб24materialoved.doc
#
14.02.2015899.5 Кб40mcad_pract.pdf
#
14.02.2015203.78 Кб25mech.doc
#
15.11.2019323.76 Кб7Meeting clients.docx