
Matematika_Zaytsev_ch2
.pdf
а)
в)
д)
4.
5.
A = {1; 32 ; 52 ;7 2 ; K}; |
|
|
|
|
б) |
В = {1 2; 2 3; 3 4; ... }; |
|||||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
C = |
|
; |
|
|
|
|
|
; |
|
|
|
|
|
; K |
; |
г) |
D = {1; –4; 9; –16; ... }; |
||||
1 5 |
5 |
|
9 |
|
|
9 13 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
5 |
|
|
|
7 |
|
|
9 |
|
|
11 |
|
|
|
|
|||||
E = |
−3; |
|
|
; |
− |
|
|
|
|
; |
|
|
; − |
|
|
; K . |
|
||||
3 |
|
5 |
|
7 |
9 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Представьте обыкновенные дроби в виде десятичной дроби:
а) 73 ; б) 3023 ; в) 73 .
Запишите в виде несократимой обыкновенной дроби:
а) 0, (6); б) 1, 0(8); в) 2, 1(34).
6. В группе из 40 студентов 30 умеют плавать, 27 умеют играть в шахматы и только пятеро не умеют ни того, ни другого. Сколько студентов этой группы умеют плавать и играть в шахматы?
7. Найти число элементов множеств
A = {x Q : x3 – 2x = 0}; B = {x R : x2 + 1 < 0}; С = {x Z : |x – 1| < 3}.
8. Для множеств A = {–3; 2; 0; –4; 1} и B = {1; 2; 5; 8} найти АU B, АI B, А \ B, B \ A.
9. Найти АU B, АI B, А \ B, B \ A для множеств A = (–2; 3) и В = [–3; 2].
10. Пусть Х – множество всех треугольников на плоскости, Х1 – множество всех равнобедренных треугольников, Х2 – множество всех равносторонних треугольников, Х3 – множество всех прямоугольных треугольников.
Найти X1 I X2 , X1 U X2 , X1 I X3 , X2 \ X1 , X3 \ X2 , X2 I X3 .
11. Описать перечислением всех элементов множества
АU B, АI B, А \ B, B \ A,
если A = {x R : x2 + x =20}; B = {x R : x2 – x – 12 = 0}.
12. Считая отрезок [0; 1] универсальным множеством, найти дополнения следующих множеств:
а) {0; 1}; б) [0; 0,5 ); в) (0,25; 0,5); г) {0} U [0,75; 1 ) .
13. Записать множества A, B и С перечислением их элементов и найти
A U B , B IC , ( A U B ) IC , A I B IC , если:
а) A – множество делителей числа 12; B – множество корней уравнения
31
x2 – 6x + 5 = 0; C – множество нечётных чисел x: 3 ≤ x ≤ 12;
б) A – множество четных чисел: 3 < x < 10; B – множество делителей числа 21; C – множество простых чисел, меньших 12.
14. Найти A U B, A I B, A IC , B UC , A I B IC , ( A U B ) IC , если
а) А = [0; 3], |
B = (1; 5), |
C = (–2; 0); |
б) A= (∞; 1], B = [ 1; +∞), C = (0; 1). |
||||
15. |
Найти z1 |
+ z2 , |
z1z2 , |
z1 – z2 , |
z1 |
, если |
|
|
|||||||
|
|
|
|
|
z2 |
|
|
|
а) z1 = 2 + 5i , z2 = 1 – 7i; |
б) z1 = 2 − 3i , z2 = 2 + 3i . |
|||||
16. |
Записать комплексное число z в алгебраической форме: |
||||||
|
−1 + |
3i 2 |
|
|
|
6 |
|
|
а) z = |
|
; |
б) z = (2 + i) . |
|||
|
|
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
17. |
Найти все значения n w , если |
|
|
|
|||
|
а) w = –1 , n = 4; |
б) w = −4 + |
48i , n = 3 . |
||||
18. |
Определить значения истинности следующих высказываний: |
||||||
|
A : π < |
11 ; |
|
|
|
|
|
B : число 6 является простым числом;
С : корни уравнений 2x2 = 16 и |x| = 2 совпадают; D : слон – насекомое;
E : существует прямоугольный треугольник со сторонами 3, 4, 5 ; F : для любого треугольника сумма внутренних углов равна 180°; G : в любую трапецию можно вписать окружность.
19. Заданы высказывания:
А : число 6 имеет 4 делителя;
В : прямая с уравнением x + y = 1 проходит через начало координат; С : все корни уравнения 3x2 + 2x – 1 = 0 являются целыми числами;
D: существует натуральное число x, удовлетворяющее условию |x – 1| < 2.
Определить значения истинности следующих высказываний:
а) ( A C ) B ; |
б) B C D ; |
||||
в) ( |
|
|
|
) C ; |
г) ( A B ) ( A D ) . |
A |
D |
||||
32

Глава 2. ФУНКЦИИ ОДНОГО АРГУМЕНТА
1.ОСНОВНЫЕ ПОНЯТИЯ
1.1Определение функции
Важную роль в математике играет понятие функции.
Если для каждого элемента x X по определённому правилу однозначно выбран элемент y Y, то говорят, что задана функция f множества X во множество Y, при этом пишут f: X → Y.
Отметим, что множества X и Y при этом могут быть и не числовыми.
В дальнейшем будем рассматривать частный случай понятия функции, а имен-
но такие функции, когда множества X, Y R , т. е. являются подмножествами множества действительных чисел.
Действительной функцией действительного аргумента (далее просто функцией), определенной на множестве X, называют соответствие или правило, которое каждому числу x X соотносит некоторое единственное число y R.
При этом множество X называют областью определения (или областью существования) функции f и обозначают D(f), точку x X – аргументом функции,
точку y R, соответствующую x, – значением функции в точке x и обозначают f(x).
Множество E(f) = {y R: y = f(x), x X} называют областью значений функции f.
Пример 1. Найти область определения и область значений функции
y = |
1 |
. |
|
1 − x2 |
|
||
|
|
|
|
• Областью определения этой функции является множество |
|||
D(f) = {x R : 1 – x2 > 0} = {x R : |
|x| < 1} = (–1, 1). |
||
Областью значений – множество E(f) = {y R : |
y ≥ 1} = [1, +∞). • |
||
Замечание. Разумеется, вместо букв x, f, y можно взять другие буквы; например, функция может быть записана в виде z = ϕ(t).
Если число a D(f), то говорят, что функция f определена в точке a. Для того, чтобы указать значение функции в фиксированной точке a, используются такие
способы записи: f(a), y(a), |
f(x)|x=a. |
|
1 |
|
|
1 − x |
|
|
Пример 2. Найти f(0), |
f(1), f(–x), f(x+1), |
|
|
f ( x ) = |
|
|||
f |
|
|
, если |
|
. |
|||
|
1 + x |
|||||||
|
|
|
x |
|
|
|
||
33

• f ( 0 ) = |
|
1 − 0 |
= 1, f ( 1 ) = |
1 − 1 |
= 0, f ( −x ) = |
1 − ( −x ) |
|
= |
1 + x |
= |
1 |
|
, |
||||||||||||
1 + 0 |
1 + 1 |
|
|
|
|
f ( x ) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 + ( −x ) 1 − x |
|
|
|||||||||||
|
1 − ( x + 1 ) |
|
−x |
|
1 |
|
1 − |
1 |
|
|
x − 1 |
|
|
1 − x |
|
|
|
|
|
||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||
f ( x + 1 ) = |
|
|
|
= |
|
|
, f |
|
|
= |
|
= |
|
|
= − |
|
|
= − f ( x ). |
• |
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||
|
1 + ( x + 1 ) |
|
2 + x |
x |
1 + |
|
|
x + 1 |
|
|
1 + x |
|
|
|
|
|
|||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.2 График функции
Множество точек G = {(x, f(x)), x X} координатной плоскости ОХY называют графиком функции f, определённой на множестве X R.
Например, графиком функции y = xk при k = 0 и k = 1 будет прямая, при k = 2
– парабола, при k = –1 – гипербола (рисунок 1).
Рисунок 1
Отметим, что не для всякой функции график будет линией в обычном представлении. Характерным примером является функция Дириxле, которая равна единице, если аргументом является рациональное число, и нулю – в противном случае, т.е.
1, если x-рациональное число |
. |
(1) |
f (x) = |
||
0, если x-иррациональное число |
|
|
Напомним, что при построении графиков функций часто используются следующие геометрические рассуждения. Если G – график функции y = f(x), то график функции:
1)y1 = – f(x) есть зеркальное отражение графика G относительно оси ОХ;
2)y2 = f(–x) – зеркальное отражение G относительно ОY;
3)y3 = f(x – a) – сдвиг G вдоль оси ОХ на величину a (вправо, если a > 0; вле-
во, если a < 0);
4) y4 = f(x) + b – сдвиг G вдоль оси ОY на величину b (вверх, если b > 0; вниз, если b < 0);
34
5)y5 = f(αx), α > 0 – сжатие G в α раз при α > 1 или растяжение Г в 1/α раз при α < 1 вдоль оси ОХ;
6)y6 = βf(x), β > 0 – растяжение G в β раз при β > 1 или сжатие Г в 1/β раз
при β < 1 вдоль оси ОY.
Таким образом, путём простых преобразований графика G исходной функции f(x) можно построить график функции вида βf(αx – a) + b, где α, β, а, b R.
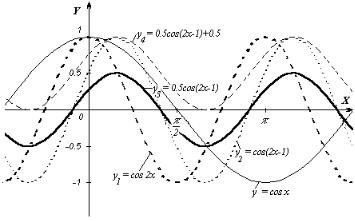
Пример 3. Построить график функции y = 0,5cos(2x – 1) + 0,5.
• График этой функции можно построить путём последовательных преобразований графика G функции y = cosx:
y1 = cos2x, y2 = cos(2x – 1) = cos2(x – 0,5), y3 = 0,5cos2(x – 0,5), y4 = 0,5cos2(x – 0,5) + 0,5.
Геометрически это приводит к следующим построениям.
1)Строим одну волну косинусоиды y = cosx (рисунок 2).
2)Отметим на графике функции y = cosx несколько точек и уменьшаем в 2 раза их абсциссы, сохраняя их ординаты неизменными. Соединив полученные точки
плавной линией, получим график функции y1 = cos2x, являющийся результатом сжатия графика функции y = cosx в 2 раза вдоль оси ОХ.
3)Переносим точки, полученные в предыдущем пункте, на величину 0,5 вправо вдоль оси ОХ. Соединив полученные точки плавной линией, получим график
функции y2 = cos2(x – 0,5), являющийся результатом сдвига графика функции y1 = cos2x на величину 0,5 вдоль оси ОХ.
4)Уменьшаем ординаты точек, полученных в предыдущем пункте, в 2 раза, сохраняя их абсциссы. Соединив полученные точки плавной линией, получим гра-
фик функции y3 = 0,5cos2(x – 0,5).
5)Сдвигая график функции y3 вдоль оси ОY вверх на величину 0,5, получим график заданной функции (рисунок 2).
Рисунок 2
35
1.3 Основные способы задания функции
Правило, позволяющее по значению аргумента находить соответствующее ему значение функции, можно указать различными способами. Рассмотрим основные.
Функция y = f(x), x X задана явным аналитическим способом, если дана формула, указывающая последовательность действий, которые надо выполнить с аргументом x, чтобы получить значение y = f(x) этой функции.
Например, формула y = x2 + 1, x R указывает два математических действия над аргументом x: «возведи x во вторую степень, а затем к полученному результату прибавь число 1». Формула y = lg( x − 1 ) , x [ 2, + ∞ ) указывает три ма-
тематических операции: «от аргумента x отними число 1, затем вычисли значение десятичного логарифма от полученного результата, затем вычисли значение квадратного корня».
Иногда рассматриваемая функция может быть задана несколькими формулами, действующими на различных участках области её определения, в которой изменяется аргумент функции. Например:
1) функция абсолютного значения числа x ( модуля x ) (рисунок 3)
−x |
при |
x < 0 |
. |
(2) |
|
y =| x |= |
x |
при |
x ≥ 0 |
||
|
|
|
|||
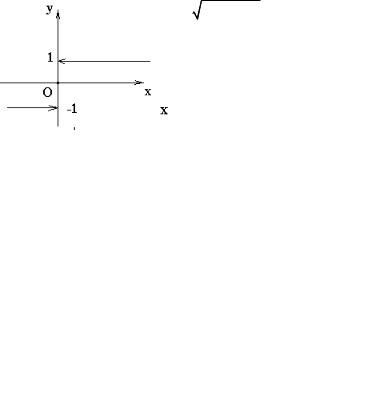
2) функция знака – “сигнум x” (рисунок 4)
−1 y = sign( x ) = 0
1
при x < 0
при x = 0 (3) при x > 0
Рисунок 3 |
Рисунок 4 |
На рисунке 4 точкой О отмечено значение функции при x = 0, а стрелка на конце линии указывает на то, что конечная точка не принадлежит линии.
Функции такого вида называют составными или кусочно-аналитическими.
Замечание. Если функция задана явным аналитическим способом с помощью формулы, но область определения функции в виде множества X не указана, то под
36

X будем всегда подразумевать множество значений аргумента x, при которых дан-
ная формула имеет смысл (естественная область определения).
Например, для функции y = x3 + x – 1 областью определения будет множество X = R = (–∞, +∞), а для функции y = lg(4 – x2) областью определения будет множество значений x, удовлетворяющих неравенству 4 – x2 > 0, т.е. X = (–2; 2).
Если зависимость y от x не задана непосредственно, а дано соотношение
F(x, y) = 0, |
(4) |
связывающее значения функции y и аргумента x, то говорят, что функция задана неявным аналитическим способом.
Отметим, что если (4) удается однозначно разрешить относительно y = f(x), то получаем ту же функцию, но уже заданную явным аналитическим способом. Так,
уравнение 2x – y3 + 1 = 0 и равенство y = 3 2x + 1 определяют одну и ту же функцию.
Когда зависимость y от x не задана непосредственно, а вместо этого даны зависимости обеих переменных y и x от некоторой третьей вспомогательной переменной t в виде:
x =α( t ) |
, |
t T R, |
(5) |
|
|||
y = β( t ) |
|
|
|
то это – параметрический способ задания функции, а переменную t называют параметром. Если из (5) удаётся исключить параметр t, то придём к функции, заданной явной или неявной аналитической зависимостью y от x.
x = 2t −1 |
, t R исключением параметра t полу- |
Например, из соотношений |
|
y = t + 2 |
|
чим явно заданную функцию y = 0,5(x + 5).
Иногда используют графический способ задания функции, когда зависимость y от x задают линией на плоскости OXY. Однако при всей наглядности он проигрывает в точности, поскольку значения аргумента и соответствующие им значения функции можно получить из графика лишь приближённо. В дальнейшем графику функции отведём роль только иллюстрации поведения функции и, поэтому, будем ограничиваться построением «эскизов» графиков, отражающих основные особенности функций.
Отметим табличный способ задания функции, когда некоторые значения аргумента и соответствующие им значения функции размещаются в таблице. Так построены известные таблицы тригонометрических функций, таблицы логарифмов и т.п. В виде таблицы обычно представляют зависимость между величинами, измеряемыми при экспериментальных исследованиях, наблюдениях, испытаниях.
Функцию можно задать алгоритмическим (программным) способом, который широко используют при вычислениях на ЭВМ.
37
1.4 Сложные и взаимно обратные функции
Нередко возникает необходимость в рассмотрении сложной функции, т.е. «функции от функции», или, как говорят, суперпозиции функций. В этом случае аргумент u функции y = f(u) не является независимой переменной, а сам зависит от другого аргумента, например, от аргумента x в виде зависимости u = g(x). То-
гда для задания зависимости y от x нужно вместо промежуточной переменной u подставить ее выражение через x, записав y = f(g(x)) = F(x).
При вычислении значения сложной функции сначала по значению x вычисляют значение промежуточной переменной u, а лишь затем – её значение y.
Функции y = f(u) и u = g(x) могут образовывать суперпозицию y = f(g(x)), если только пересечение области определения первой из них с областью значений
второй не является пустым множеством, т.е. D( f ) I E( g ) ≠ . Так функции f ( u ) = u − 5 и u = g(x) = cosx не определяют сложную функцию f(g(x)), так как D(f) = [5, +∞), E(g) = [–1; 1], D( f ) I E( g ) = .
Областью определения D(f(g(x))) сложной функции является вся область определения функции g(x), либо та её часть, для которой значения u = g(x) не выходят за пределы области определения функции f(u), т.е.
D( f ( g( x ))) ={x : x D( g ) u = g( x ) D( f )}.
Пример 4. Найти область определения суперпозиции функций f и g, если f ( u ) = u , g( x ) = sin2 x − 1 .
• D(g) = R, E(g) = [–1; 0], D(f) = [0, +∞). Имеем D( f ) I E( g ) ={0}.
Поэтому
D( f ( g( x ))) ={x R : g( x ) =0} ={x : sin2 x −1 =0} ={x =( 2k +1 )π / 2 : k Z}. •
Сложная функция может быть суперпозицией более чем двух функций.
Пример 5. Найти f( f( f(x))), если |
f ( x ) = |
|
1 |
|
|
. |
|
|
|
|||||||||||
|
1 − x |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
• Вначале найдём f ( f ( x )) = |
f |
|
|
1 |
= |
|
|
1 |
|
= |
x − 1 |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
||||||||||||
|
|
|
|
|
1 − x |
|
|
|
|
1 − |
|
|
|
x |
|
|||||
|
|
|
|
|
|
|
1 |
− x |
|
|
||||||||||
x − 1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Итак, f ( f ( f ( x ))) = f |
|
|
= |
|
|
|
|
|
|
|
|
= x . • |
|
|
|
|||||
x |
|
|
|
|
x − 1 |
|
|
|
||||||||||||
|
|
|
1 |
− |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть функция y = f(x) такая, что различным значениям аргумента x из области определения D(f) соответствуют различные значения функции f(x) в области значений E(f).
38
Тогда для любого числа y E(f) можно указать единственное число x X, что y = f(х), т.е. на множестве E(f) можно определить новую функцию, называемую
обратной к функции (или обратной для функции) f и обозначаемую символом f −1 . Функции f и f −1 называют взаимно обратными.
Из определения обратной функции следует, что
x D( f ) ( f −1 )−1 = f , f −1 ( f ( x )) = x ,y E( f ) f ( f −1 ( y )) = y .
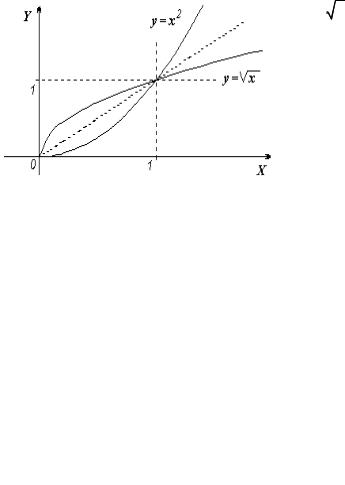
Пример 6. Найти обратную функцию для функции y = x2 , x [0, +∞).
• Для нахождения обратной функции выразим x через y: x = y .
Обратная функция f −1 ( y) = y определена на множестве Y ={y R : y ≥ 0}. Заметим, что для функции y = x2, x (–∞, 0] обратной функцией является
функция f −1 ( y) = − y . А для функции y = x2, x R обратная функция не
определена, так как в этом случае f(x) = f(–x), т.е. разным значениям аргумента x соответствуют одинаковые значения функции. •
Если функция x = f −1 ( y) является обратной к функции y = f(x), то множест-
во точек плоскости, определяющих график той и другой функции, одно и то же, т.е. графики обеих функций совпадают.
Но если потребовать, чтобы аргумент обратной функции был также обозначен буквой x, то надо вместо функции x = f −1 ( y) рассматривать функцию
y = f −1 ( x) . В этом случае графики взаимно обратных функций будут различны-
ми (один будет зеркальным отражением другого относительно биссектрисы 1-й и 3-й четверти координатной плоскости).
Графики взаимно обратных функций, рассмотренных в примере 6, изображены на рисунке 5.
Рисунок 5
39

2. НЕКОТОРЫЕ СВОЙСТВА ФУНКЦИЙ
2.1 Периодические функции
Периодом функции f(x), определённой на множестве X R, называют действительное число T > 0, такое, что при любом x Х числа x + T и x – T также принадлежат множеству Х и справедливо равенство f(x + T) = f(x – T) = f(x).
Функцию, имеющую период, называют периодической.
Замечание. Числа nT n N также будут периодом этой функции, так как f(x + nT) = f(x +(n – 1)T + T) = f(x+(n–1)T) = f(x + (n–2)T + T) =
=f(x + (n–2)T) = ... = f(x) x X.
Вдальнейшем под периодом функции будем понимать наименьший из её периодов.
Пример 7. Пусть функция y = f(x) имеет период T. Найти период функции g(x) = f(ax + b), где a и b – постоянные и a > 0.
• Так как функция f(x) периодическая с периодом T, то |
|
|
|
|||
|
T |
|
T |
|
||
g(x) = f(ax + b) = f(ax + b + T) = f(a x + |
|
|
+ b ) = g x + |
|
|
, |
|
|
|||||
|
a |
|
a |
|
||
поэтому период функции g(x) равен Ta . •
Очевидно, что для построения графика функции f(x) с периодом T, определённой на множестве X R, достаточно построить её график на любом отрезке
[a, a + T] X, где а Х – некоторое число, а затем продолжить его вдоль коор-
динатной оси OX на отрезки [a+Т, a +2T], [a+2Т, a +3T], … .
2.2 Монотонные функции
Пусть функция f(x) определена на множестве X R и x1, x2 – любые две точки этого множества, для которых выполнено условие x1 < x2.
Функцию f(x) называют на этом множестве
1)возрастающей, если f(x1) < f(x2);
2)неубывающей, если f(x1) ≤ f(x2);
3)убывающей, если f(x1) > f(x2);
4)невозрастающей, если f(x1) ≥ f(x2).
Во всех четырех случаях функцию называют монотонной на множестве X, причём в случаях 1) и 3) говорят, что функция строго монотонна, а в случаях 2) и 4) – просто монотонна.
Очевидно, что для строго монотонной функции различным значениям аргумента обязательно будут соответствовать различные значения функции, поэтому будет существовать обратная к ней функция, тоже строго монотонная.
Пример 8. Определить интервалы монотонности следующих функций:
40
