Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Matematika_Zaytsev_ch2

.pdf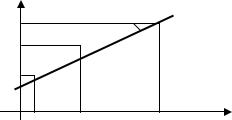

Скачиваний:

Добавлен:

14.02.2015

Размер:

2.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2321 22 23 > Следующая >>>

3.6 Метод наименьших квадратов

Пусть на основании эксперимента необходимо установить функциональную зависимость между двумя переменными величинами x и y. Например, между временем движения и расстоянием, температурой и удлинением металлического стержня и т. д. По результатам измерения составлена таблица:

x	x1	x2	. . .	xi	. . .	xn
y	y1	y2	. . .	yi	. . .	yn

Y		y=ax+b
yn			•
yi	•	•	•
y1 •	• • •	•	•
y1 •	•
	•
x1	xi		xn
	Рисунок 9

Установим вид функции y = f(x) по характеру расположения на координатной плоскости экспериментальных точек. Пусть, например, точки, взятые из таблицы, расположены так, как показано на рисунке 9. В данном случае можно предположить, что между x и y существует линейная зави-

Xсимость, выражающаяся формулой y = ax + b (ограничимся только ли-

нейной зависимостью).

Так как точки (xi, yi) не лежат точно на прямой, то, в общем случае, yi – (axi + b) = δi ≠ 0, i = 1, …, n (числа δi называются погрешностями).

Поставим задачу: подобрать коэффициенты a и b таким образом, чтобы сумма квадратов погрешностей

n	n
S( a ,b ) = ∑[ yi − ( axi + b )]2 = ∑δi2
i =1	i =1

была наименьшей (метод наименьших квадратов). Здесь xi, yi – заданные числа, а коэффициенты a и b – неизвестные числа, подлежащие определению, исходя из условия минимума S(a, b) − функции двух переменных a и b.

Таким образом, задача свелась к нахождению значений a и b, при которых функция S(a, b) имеет наименьшее значение.

Решаем эту задачу. Имеем

∂S	n	∂S	n
∂S	= −2∑[ yi − axi − b ] xi ,	∂S	= −2∑[ yi − axi − b ] .
∂a	i =1	∂b	i =1

Приравнивая эти частные производные нулю, получаем линейную систему двух уравнений с двумя неизвестными a и b:

	n	n	n
a ∑ xi2 + b ∑ xi = ∑ xi yi					.	(21)
	i =1	i =1	i =	1	.	(21)
	n		n
a ∑ xi		+ b n = ∑ yi
	i =1		i =1
		197

Система (21) называется нормальной системой метода наименьших квадратов.

Из этой системы легко определить числа a и b, а, значит, и уравнение y = ax + b исходной прямой.

Покажем, что функция S(a, b) в найденной точке M(a, b) имеет единственный экстремум (минимум), т. е. наименьшее значение.

∂

S2 = 2n , поэто-

Действительно, A =

= 2∑xi2 , B =

= 2∑xi , C =

∂a∂b

∂a

i =1

∂b

n n

му, D = A C − B2 = 4n∑xi2 − 4

∑xi

= 2∑∑( xi − x j

)2 > 0 (последнее

i =1

i =1 j=1

равенство советуем читателю доказать самостоятельно, используя, например, метод математической индукции по n). Так как A > 0, то в точке M(a, b), где (a, b) – решение системы (21), функция имеет наименьшее значение.

Пример 22. Пусть в результате эксперимента получены пять значений искомой функции y при пяти значениях аргумента x:

x	–2	0	1	2	4
y	0,5	1	1,5	2	3

Найти функциональную зависимость между x и y в виде линейной функции

y= ax + b.

•Вначале вычислим

5			5
∑xi = −2 + 0 + 1 + 2 + 4 = 5 , ∑yi = 0 ,5 + 1 + 1,5 + 2 + 3 = 8 ,
i =1			i =1
5		5
∑xi2 =(−2)2 +02 +12 +22 +42 =25 ,		∑xi yi =(−2) 0,5+0 1+1 1,5+2 2+4 3=16,5.
i=1		i=1
Система (21) принимает вид:
25a + 5b = 16 ,5				a = 0,425
	+ 5b	= 8
5a	+ 5b	= 8		b = 1,175.

Следовательно, y = 0,425x + 1,175 – уравнение искомой прямой. •

4.ЗАДАЧИ

4.1Задачи с решениями

1. Найти области определения следующих функций: 1) z = arcsin(x + y); 2) u = ln(1− x− y − z).

• 1) Область определения функции z двух независимых переменных x и y есть

совокупность значений x и y, удовлетворяющих неравенству: −1 ≤ x + y ≤ 1. На плоскости OXY эта область представляет полосу, ограниченную прямыми

x + y = − 1 и x + y = 1.

198

2) Функция u трёх независимых переменных x, y, z определена при

1− x − y − z > 0, т. е. при x + y + z < 1. Следовательно, областью определения функции u является та часть пространства, которая содержит точки, лежащие по одну сторону от плоскости x + y + z = 1 (там, где находится начало координат

O(0; 0; 0)). •

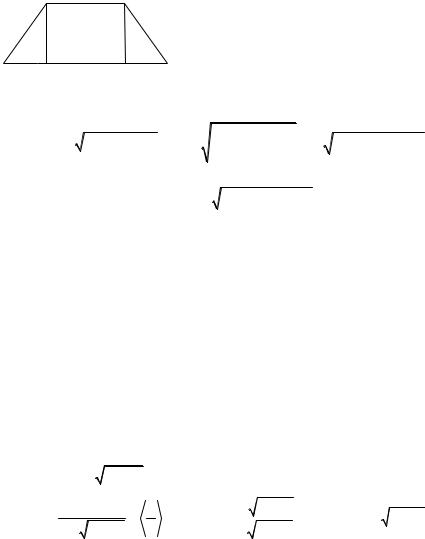
2. Выразить площадь S равнобочной трапеции как функцию длин её сторон (x и y – длины оснований, z – длина боковой стороны). Найти область определения этой функции.

•

Как

известно,

площадь трапеции

x + y

S =

h , где h – высота трапеции. Пусть

x = BC, y = AD и x < y (рисунок 10).

y − x

Для равнобочной трапеции ND =

y−x

По теореме Пифагора

Рисунок 10

CN = CD2 − ND2

h =

z2 −

( y − x )2

4z2 − ( y − x )2 .

Итак, функция

x + y

S =

4z2

− ( y − x )2 .

Область определения этой функции определяется условиями:

y − x

4z2− (y − x)2 > 0, x > 0, y > x, z > 0.

Отсюда, z >

, x > 0,

y > x, z > 0 – область определения функции S. •

3. Построить линии уровня функции z =

•Линии

уровня

данной

функции

определяются

уравнением

= C , C R y = Cx,

x ≠ 0

– множество «проколотых» в точке О(0; 0)

прямых, проходящих через точку O(0; 0). Давая C различные числовые значения,

можно построить ряд таких линий. •

4. Найти пределы:

2 x

2 + y2

x2 − y2

1) lim

;

2) lim ( 1 + x

+ y

)

;

lim

3 − xy

+ 9

x2 + y2

x→0

→0

y→0

→0

•1) lim

= 0

= lim

xy( 3 +

xy +9 )

= − lim( 3 +

xy +9 ) = −6.

y→0 3 − xy +9

y→0

y→0 ( 3 )

−( xy +9 )

x→0

199

∞

2 2

lim( 1 + x

+ y

)

x2 + y2

t→ 0 =

=( 1 ) =

Замена: x +y = t; при x→ 0, y→ 0

x→0

y→0

= lim( 1 + t )

= e.

t→0

1 −

y 2

− y

lim

= lim

= Рассмотрим изменение x и y вдоль,

y 2

x→0

y→0

y→0 1

например, прямой y = kx

= lim

1 − k 2

+ k 2

1 + k 2

x→0

y→0

Результат имеет различные значения в зависимости от выбранного k, поэтому рассмотренный предел не существует. •

5. Найти точки разрыва функций:
1)	z =	xy + 1		;	2)	z =	x2	+ y2		;
		x2	+ y2				( x + y )( y2
									− x )

			1
sin				, ( x, y ) ≠ ( 0; 0 )	3	− x − y, ( x,	y ) ≠ ( 1; 2 )
sin		x2	+ y2	, ( x, y ) ≠ ( 0; 0 )	3	− x − y, ( x,	y ) ≠ ( 1; 2 )	.
3) z =		x2	+ y2		; 4) z =	1 , x =	1, y = 2	.
	1	,		x = 0, y = 0		1 , x =	1, y = 2
	1	,		x = 0, y = 0

• 1) Функция определена на плоскости OXY во всех точках, кроме точки O(0; 0), поэтому в этой точке функция разрывная. Во всех других точках функция непрерывная.

2) Функция не определена в тех точках плоскости OXY, где x + y = 0 или y2− x = 0. В первом случае точки разрыва лежат на прямой y = − x, во втором случае – на параболе y2 = x.

3)Функция разрывная в точке O(0; 0), так как она определена в окрестности этой точки и в самой точке, но не имеет предела при M(x, y)→ O(0; 0). Во всех других точках функция непрерывная.

4)Функция разрывная в точке M1(1; 2), так как она определена вблизи точки и

всамой точке, но её предел при M(x, y)→ M1 не совпадает со значением функции

в точке M1:	lim z = 0 ≠ z( M1 ) = 1 .			•
	M →M1
6. Найти частные производные 1-го порядка функций:
1)	z = x2 − xy +	y	+ y2 − 1 ;	2) u = x y z .

		x
				200

•1) Считая z функцией только одного аргумента x (если y фиксировать),

находим z′x = 2x − y − xy2 .

Аналогично, считая z функцией только y (если x – постоянная величина), по-

лучим

z′y = −x +

+ 2 y .

Считая u функцией только x, затем только y , затем только z, получим

′

y z −1

′

y z

′

y z

ux = y z x

, uy = x

ln x

z , uz = x

ln x y

. •

7. Вычислить значения частных производных 1-го порядка функции z = ln(x2 – y2) при x = 1, y = 0.

• Вначале находим частные производные, а затем вычисляем их значения при

указанных x и y:

z′x =

2 x

, z′y =

−2 y

z′x ( 1; 0 ) = 2,

z′y ( 1; 0 ) = 0.•

x2 − y2

8. Найти частные производные 1-го и 2-го порядка функции z = arctg

•Имеем:

z′x =

z′y =

−

= −

+ y2

y 2

Дифференцируем вторично:

z′′xx =

′

( x

)

−1 ′

2 xy

−

= − y

( x

2 2

′

)

z′′xy =

−

= −

1 ( x2 + y2 ) − y 2 y

y2 − x2

= z′′yx ,

( x

2 2

( x

)

z′′yy =

′

( x

)

−1

′

2 xy

= x

= −

.•

+ y

( x

2 2

)

9. Проверить, что функция z = e

удовлетворяет уравнению z′x −z′y + yz′′xy =0.

• Вычислим требуемые производные:

z′x = e y

,z′y = e y

−

201

−1 ′

z′′xy = e

= e

−

+ e

−

= e

−

+ 1

Запишем и преобразуем выражение:

z′x −z′y + yz′′xy =e y

−e y

−

+ y e y −

=e y

−

−1

=0,

y y

что и требовалось. •

10. Найти дифференциалы 1-го и 2-го порядков функции z = 2x2y3.

• Так как z′x = 4 xy3 ,

z′y = 6 x2 y2 , то dz = z′xdx + z′ydy = 4 xy3dx + 6 x2 y2dy .

Имеем z′′xx = 4 y3 ,

z′′xy = z′′yx = 12 xy2 ,

z′′yy = 12 x2 y , поэтому

d 2 z = z′′xx ( dx )2 + 2z′′xydxdy + z′′yy ( dy )2 = 4 y3 ( dx )2 + 24xy2dxdy + 12x2 y( dy )2 .•

11. Найти приближенное значение 1,942 e0,12, исходя из значений функции f(x, y) = x2ey в точке M0(2; 0) и заменяя её полное приращение полным дифференциалом (вычисления выполнять с точностью до 0,01).

• Рассмотрим точку M(1,94; 0,12), в которой нужно вычислить значение функ-

ции. Тогда ∆x = 1,94 −2 = − 0,06; ∆y = 0,12 − 0 = 0,12; f(M0) = 22 e0 = 4;

fx′( M0	) = 2 xe y	M0		= 2 2 e0 = 4 ;		f y′( M0 ) = x2e y	= 22 e0 = 4 .
		M0					M0
Используя формулу (7), получим
			1,942e0,12 ≈ 4 + 4 (− 0,06) + 4 0,12 = 4,24. •
12. Найти производные сложных функций:
1)	z = x sin	x	,	x = 1 + 3t , y =		1 + t2 ;
1)	z = x sin		,	x = 1 + 3t , y =		1 + t2 ;
		y
2)	z = x sinucos v, u = ln( x2 + 1 ), v = − 1 − x2						;
3)	z = x2 y2 , x = u + 2v , y =				u	;
3)	z = x2 y2 , x = u + 2v , y =				v	;
					v

4) u = xy – 2x + y + z2 – 1, x = 2t1 , y = t1 – t2 , z = t22 − 1 .

• 1) Функция z – сложная функция одной независимой переменной t, а x и y – промежуточные переменные. Поэтому

∂ z

sin

+ x cos

+ xcos

−

∂ x dt

∂ y dt

2) Функция z – сложная функция одной независимой переменной x,

1 + t2

содержит

три промежуточные переменные: x, u, v (первая промежуточная переменная совпадает с независимой переменной). Имеем

202

∂ z

+ ∂ z

∂ z

∂ x

∂ v

∂ u

= sin u cos v 1 + x cos u cos v

2 x

− x sin u sin v

x 2 +

1 − x 2

= sin u cos v + cos u cos v

2 x 2

− sin u sin v

x 2

x 2 +

1 − x 2

3) Функция z – сложная функция двух независимых переменных u, v, а x и y – две промежуточные переменные. Найдём

∂ z

∂ x

∂ z

∂ y

= 2 xy2

1 + 2 x2 y

∂ u

∂ x

∂ u

∂ y

∂ u

∂ z

∂ x

∂ z

∂ y

= 2 xy

2 + 2 x

−

∂ v

∂ x

∂ v

∂ y

∂ v

4) Функция u – сложная функция двух независимых переменных t1, t2, а x, y, z – три промежуточные переменные. Вычислим:

∂u

∂x

+∂u

∂ y

+∂u

∂z

=( y−2) 2+( x+1) 1+2z 0 = x+2y−3,

∂t

∂x

∂ y

∂z

•

∂u

=∂u

∂x

+∂u

∂ y

+∂u

∂z

=( y−2) 0+( x+1) (−1)+2z 2t

=−x+4zt

−1.

∂t2

∂x ∂t2 ∂ y ∂t2 ∂z ∂t2

13. Найти указанные производные неявных функций:

1) x + y = a ,			dy	;		2) eu		= cos v cos t ,
1) x + y = a ,			dx	;		2) eu		= cos v cos t ,
			dx
•1) Преобразовав данное уравнение к виду x +											y −
вую часть этого уравнения через F(x, y), имеем
					Fx′		1
	dy	= −			Fx′	= −	2	x	= −	y	.
	dx	= −			Fy′	= −	1		= −	x	.
							1
							2	y
							2	y

∂∂ut , ∂∂ uv .

a = 0 и обозначив ле-

2) Запишем уравнение в виде eu − cosv cost = 0. Обозначим

F(u, v, t)= eu − cosv cost. Тогда
∂ u	= −	Ft′	= −	−cosv( − sint )	= −cosv sint	e−u ,
∂ t		Fu′		eu

∂ u	= −	Fv′	= −	−( −sinv )cos t	= − sinv cos t	e−u .
∂ v		Fu′		eu

Производные можно преобразовать, учитывая, что eu = cosv cost: 203

∂ u	= −tgt ,	∂ u	= −tgv . •
∂ t		∂ v

14. Представить функцию f(x,y)=ln(1+3x+2y) по формуле Маклорена при

n=2.

• Имеем f(0, 0)= 0, df =

∆x +

∆y , df(0, 0) = 3∆x+2∆y,

1+ 3x + 2y

1+ 3x + 2 y

d2 f = −

( ∆x )2 −

∆x∆y −

( ∆y )2

;

(1 + 3x +

+ 3x + 2y )

2 y )

d2f(0, 0) = –9(∆x)2 – 12∆x∆y – 4(∆y)2.

Заменяя ∆x на x и ∆y на y, по формуле (15/) получаем

ln( 1 + 3x + 2 y ) = 3x + 2 y −

( 9 x2 + 12xy + 4 y2 ) + r

.•

15. Найти производную функции u = x2 – 3yz + 5 в точке M0(1; 2; –1) в направлении, составляющем одинаковые острые углы со всеми координатными осями.

• Для направляющих косинусов любого направления выполняется равенство

cos2α + cos2β + cos2γ = 1. Так как α = β = γ			0 ;	π	, то 3cos2α = 1. Отсюда
				2
следует cosα = cos β = cosγ =	1	. Имеем
следует cosα = cos β = cosγ =	3	. Имеем
	3

u′x = 2 x, u′y = −3z, uz′ = −3 y, u′x ( M0 ) = 2, u′y ( M0 ) = 3, uz′( M0 ) = −6.

Согласно формуле (16/), получим:	∂u		= 2	1	+ 3	1	− 6	1	= −	1	.

	∂s	M0		3		3		3		3

Знак минус показывает, что функция в данной точке и в данном направлении убывает. •

16. Найти единичный вектор нормали к поверхности x2 + y2 + z2 = 9 в точке

M0(2; –2; 1).

• Как было показано, градиент функции u = x2 + y2 + z2 является вектором нормали к поверхности x2 + y2 + z2 = 9 в точке M0, так как эта поверхность является поверхностью уровня u = 9 функции u, проходящей через точку M0.

Так как u′x =2x, u′y =2y, uz′ =2z , то u′x ( M0 ) = 4, u′y ( M0 ) = −4, uz′( M0 ) = 2 .

Поэтому grad u(M0) = {4; –4; 2} = 2{2; –2; 1},						grad u(M0) = 6.
Итак, единичный вектор нормали имеет вид:
n = ±	1		grad u( M0 ) = ±	1	2{2;−2;1} = ±		2	; −	2	;
	grad u( M0 )						3		3
		6

3 .

Получено два вектора нормали: внешней и внутренней, т. е. один направлен вне сферы x2 + y2 + z2 = 9, другой – внутрь. •

204

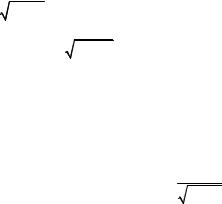
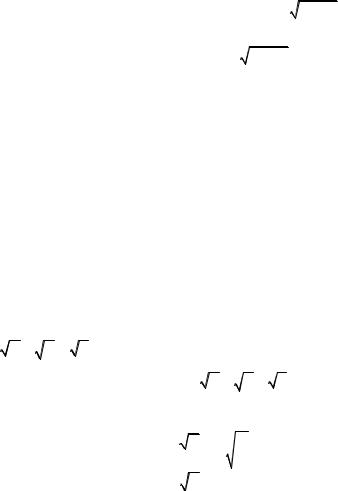
17. Написать уравнение касательной плоскости и нормали к поверхности 3xyz – z3 = a3 в точке, для которой x = 0, y = a.

• Найдём аппликату точки касания, подставив x = 0, y = a в уравнение поверхности: – z3 = a3, отсюда z = – a. Таким образом, M0(0, a, –a) – точка касания. Обозначим F(x, y, z)=3xyz – z3– a3 и найдём производные и их значения в точке

M0:

Fx′ =3yz, Fy′ =3xz, Fz′=3xy −3z2 , Fx′( M0 )=−3a2 , Fy′( M0 )=0, Fz′( M0 )=−3a2 .

Применяя формулу (19), получим уравнение касательной плоскости:

– 3a2(x – 0) + 0(y – a) – 3a2(z + a) = 0 или x + z + a = 0.

Согласно формуле (20), получим уравнения нормали:

x − 0	=	y − a	=	z + a	или	x	=	y − a	=	z + a	. •
−3a2		0		−3a2		1		0
									1

18. Исследовать на экстремум функцию z = x3 + 3xy2 – 15x – 12y.

• Найдём частные производные первого порядка:

z′x = 3x2 + 3 y2 − 15, z′y = 6 xy − 12 .

Ищем критические точки, приравнивая эти производные нулю:

	3x	2	+ 3 y	2	− 15 = 0	M1 ( 1;2 ),	M2 ( 2;1 ),	M3 ( −1;−2 ), M4 ( −2;−1 ) –
	3x		+ 3 y		− 15 = 0	M1 ( 1;2 ),	M2 ( 2;1 ),	M3 ( −1;−2 ), M4 ( −2;−1 ) –
6 xy − 12 = 0
критические точки.
	Найдём частные производные второго порядка:
						′′	′′	′′	= 6 x .
						zxx = 6 x, zxy = 6 y, zyy			= 6 x .

Воспользуемся критерием Сильвестра в каждой критической точке.

1)				′′	) =6 ,	′′	= 12 ,	′′	) =6 ,
	Точка M1(1; 2): A1 = zxx ( M1					B1 = zxy ( M1 )		C1 = zyy ( M1
D = A C − B2				= −108 <0 . Значит, в точке M1 экстремума нет.
1	1	1	1	′′		′′	) = 6 ,	′′		) =12 ,
2)					) = 12
	Точка M2(2; 1): A2 = zxx ( M2					, B2 = zxy ( M2		C2 = zyy ( M2

D2 = A2C2 − B22 = 108 > 0 . В точке M2 функция имеет экстремум – минимум, так как A2 > 0. Минимум равен z(M2)= –28.

3)Точка M3(–1; –2): A3= – 6, B3= –12, C3= – 6, D3= – 108 < 0. Экстремума

нет.

4)Точка M4(–2; –1): A4= –12, B4= –6, C4= –12, D4 = 108 > 0. Функция в

точке M4 имеет экстремум – максимум (так как A4 < 0), равный z(M4) = 28. •

19. Найти наименьшее и наибольшее значения функции z = x2 – y2 + 2 в круге x2 + y2 ≤ 1.

• 1) Найдём критические точки функции, лежащие внутри круга, и вычислим её значения в этих точках:

205

z′	= 2 x = 0		O( 0;0 ) – критическая точка внутри
z′x = 2 x , z′y = −2 y x	= −2 y =	0	O( 0;0 ) – критическая точка внутри
z′y	= −2 y =	0

круга, z(O)=2.

2) Найдём наименьшее и наибольшее значения функции на границе L заданной области – на окружности x2 + y2 = 1. Так как из уравнения окружности следует

y2 = 1– x2, x [–1; 1], то функция z на границе L становится функцией одной пе-

ременной x: z = x2 – (1 – x2) + 2 = 2x2+ 1, x [–1; 1].

Наименьшее и наибольшее значения этой функции на отрезке [–1; 1] и будут искомыми наименьшим и наибольшим значениями функции z(x, y) на границе L.

Так как dxdz = 4 x , то dxdz = 0 при x = 0. Эта единственная критическая точка

лежит внутри данного отрезка. Значение z(0) = 1. Вычислим значение z(x) на кон-

цах отрезка: z(–1) = z(1) = 3.

Итак, наименьшее значение функции z(x) на отрезке [–1; 1] равно 1 при x = 0, а наибольшее значение z(x) на [–1;1] равно 3 при x = ±1 (или, что тоже, наименьшее значение функции z(x,y) на границе L равно 1 в точках M1(0;–1), M2(0;1), а наибольшее значение функции z(x, y) на границе L равно 3 в точках M3(–1; 0),

M4(1; 0)).

3) Сравнивая значение z во внутренней критической точке O(0; 0) с ее наименьшим и наибольшим значениями на окружности, заключаем: наименьшее и наибольшее значения функция принимает на границе (соответствующие значения уже указаны). •

20. Найти наибольшее значение для произведения u = xyzt неотрицательных чисел x, y, z, t при условии, что сумма их сохраняет постоянную величину:

x + y + z + t = 4c.

• Выразим t из данного условия: t = 4c – x – y – z и подставим в выражение для u: u = xyz(4c – x – y – z).

Имеем функцию u от трёх независимых переменных x, y, z в трёхмерной области, определенной системой неравенств:

x ≥ 0, y ≥ 0, z ≥ 0, x + y + z ≤ 4c.

Геометрически эта область представляется в виде треугольной пирамиды, огра-

ниченной плоскостями x = 0, y = 0, z = 0, x + y + z = 4c.

Вычисляем частные производные функции u и приравниваем их нулю:

u′x = yz( 4c − 2 x − y − z ) = 0u′y = zx( 4c − x − 2 y − z ) = 0uz′ = xy( 4c − x − y − 2z ) = 0.

Советуем убедиться, что эта система внутри рассматриваемой области имеет только одно решение x = y = z = c, а, значит, t = c. Поэтому у функции u имеется только одна внутренняя критическая точка M(c, c, c).

206

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2321 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.20151.73 Mб316matem-up1.pdf
#
14.02.201554.78 Кб17Matematika-i-statistika-12-RiSO-B.doc
#
14.02.2015543.23 Кб31matematika_ekzamen - .doc
#
14.02.20152.69 Mб320matematika_metod_posobie.docx
#
14.02.20151.69 Mб234Matematika_ryad.doc
#
14.02.20152.17 Mб54Matematika_Zaytsev_ch2.pdf
#
14.02.20158.95 Mб92matematike_fepo_s_otvetami.doc
#
24.08.20193.22 Mб25materialoved.doc
#
14.02.2015899.5 Кб40mcad_pract.pdf
#
14.02.2015203.78 Кб25mech.doc
#
15.11.2019323.76 Кб7Meeting clients.docx