Matematika_Zaytsev_ch2

5512 = 0,2181818 ... = 0,2( 18 ) – десятичная периодическая дробь. •

Пример 2. Обратить в обыкновенные дроби десятичные периодические дроби:

а) 0,(13); б) 2,(273); в) 0,2(54).

• а) Положим x = 0,(13). Умножим «чистую» периодическую дробь x (период начинается сразу после запятой) на 100, чтобы запятая переместилась на период вправо: 100x=13,(13). Затем вычтем x из 100x: 100x – x = 13,(13) – 0,(13) = 13. Отсюда 99x = 13, x = 9913 .

б) x = 2,(273). Эта чистая периодическая дробь содержит три цифры в периоде. Умножив x на 1000, получим 1000x=2273,(273). Далее имеем:

1000x – x = 2273,(273) – 2,(273) = 2271. Поэтому x = 2271999 = 757333 .

в) Вначале не чистую периодическую дробь x = 0,2(54) переведем в чистую периодическую дробь: 10х = 2,(54). Затем 10х 100 = 254,(54). Далее

1000х – 10х = 254,(54) – 2,(54) = 252. Отсюда 990х = 252, x = 990252 = 1455 . •

Кроме бесконечных десятичных периодических дробей существуют и непериодические. Такова, например, дробь 0,1010010001 ... (после первой единицы – один нуль, после второй – два и т.д.).

Примем, что каждая бесконечная десятичная непериодическая дробь является представлением некоторого нового, не рационального числа. Множество всех этих чисел называют множеством иррациональных чисел. Вместе с рациональными числами иррациональные числа образуют множество действительных чисел R.

В качестве примера иррационального числа можно привести число 2 . Покажем, что это число не является рациональным, т.е. нет такой рациональной дроби

ве считать эту дробь несократимой. Так как m2 = 2n2, то число m2 – чётное, а, значит, и m – чётное: m = 2k, k Z. Подставляя вместо m его выражение, найдем 4k2 = 2n2, отсюда n2 = 2k2. Это означает, что и n – чётное число. Итак, пришли к

противоречию с тем, что mn – несократимая дробь. Полученное противоречие доказывает наше утверждение.

11

Отметим, что между рассмотренными числовыми множествами имеются отношения:

N Z Q R,

т.е. множества натуральных, целых, рациональных, иррациональных чисел являются подмножествами множества действительных чисел.

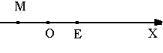
Для геометрического изображения множества действительных чисел рас-

смотрим прямую линию с выбранной на ней точкой О (точка отсчёта). Выберем любую точку E, лежащую на прямой справа от точки О. Длина отрезка |OE | задает единицу масштаба. Точка О делит прямую на две части: положительную полуось, где лежит точка E, и отрицательную полуось (рисунок 1). Такую прямую на-

зывают координатной осью ОХ. Координатой точки М на этой оси называют длину отрезка ОМ, взятую со знаком «+», если точка М лежит на положительной полуоси, и со знаком «–», если точка М лежит на отрицательной полуоси.

Очевидно, что каждой точке М на оси ОХ соответствует число х – ее координата. И, обратно, каждому действительному числу на оси ОХ соответствует точка, для которой это действительное число является ее координатой.

Всякий раз, когда это потребуется, будем считать, что между действительными числами и точками некоторой прямой установлено такого рода соответствие.

Рисунок 1

Таким образом, множество всех действительных чисел можно рассматри-

вать как числовую прямую. Отождествление действительных чисел с точками на числовой прямой будет в дальнейшем очень полезным.

Замечание. Множество R часто пополняют двумя элементами, обозначаемыми символами «+∞ » («плюс бесконечность») и «–∞ » («минус бесконечность»). При этом полагают, что – ∞ < x < +∞ . В этом случае говорят о расширенной числовой прямой. Элементы – ∞ и +∞ называют бесконечно удалёнными точками такой прямой. Объединение элементов +∞ и – ∞ обозначают просто ∞.

Очень часто будут использоваться подмножества множества действительных чисел под названием числовые промежутки:

(a, b) = {x R : a < x < b} – открытый промежуток (интервал), [a, b] = {x R : a ≤ x ≤ b} – замкнутый промежуток (отрезок),

(a, b] = {x R : a < x ≤ b} и [a, b) = {x R : a ≤ x < b} – полуинтервалы, (a, +∞) = {x R : x > a} и (– ∞, a) = {x R : x < a} – бесконечные проме-

жутки,

(–∞, +∞) = R – числовая прямая.

Любой интервал (a, b), содержащий некоторую точку x0 , называют окрестностью этой точки и обозначают U( x0 ) .

12

Точку x0 , расположенную в середине окрестности (a, b), в этом случае имену-

ют центром окрестности, а расстояние ε = b −2 a – радиусом окрестности. Тогда

множество {x R : |x – x0 | < ε} называется ε – окрестностью точки x0 и обозначается Uε ( x0 ) .

На расширенной числовой прямой вводят понятие окрестности для бесконечно удалённых точек – ∞ и +∞, тем самым уравнивая эти точки с конечными при рассмотрении многих вопросов. Пусть число М > O. Тогда

U( +∞ ) = {x R: x > M}, U( −∞ ) = {x R: x < – M}, U( ∞ ) = {x R: | x| > M}.

Итак, на множестве действительных чисел выполнимы операции сложения, вычитания, умножения, деления, извлечения корней из положительных чисел. Однако остались и невыполнимые на этом множестве операции, например, извлечение квадратного корня из отрицательного числа. Значит, имеется потребность в дальнейшем расширении понятия числа, в появлении новых чисел, отличных от действительных.

1.3 Множество комплексных чисел

Комплексным числом называется запись вида x + iy, где x, y R, a i – символ, который называют мнимой единицей, причём i2 = – 1 или i = −1 .

Два числа z1 = x1 + iy1 и z2 = x2 + iy2 называются равными в том и только в том

случае, когда x1 = x2 , y1 = y2 .

Пусть z = x + iy. Действительные числа x и y называются действительной и мнимой частями комплексного числа z: x = Re z, y = Im z.

Если y = 0, то z = x является действительным числом. Если х = 0, то z = iy

называется чисто мнимым числом.

Таким образом, множество действительных чисел R является частью множества комплексных чисел C: R C.

Модулем комплексного числа z называется неотрицательное действительное число z = x2 + y2 .

Сопряжённым числом z для числа z называется комплексное число z = x − iy ,

т. е. Re z = Re z, Im z = −Im z, z = z .

Пример 3. Решить уравнение z3 = 1 .

• Запишем данное уравнение в виде z3 −1 = 0 или, что равносильно, в виде ( z −1 )( z2 + z + 1 ) = 0 . Действительное число z1 = 1 является корнем данного уравнения и определяется из условия z −1 = 0 . Попробуем отыскать другие кор-

13

ни, решая квадратное уравнение z2 +z + 1 = 0: z2 ,3 = −1 ±2 −3 . На множестве действительных чисел R извлечение квадратного корня из отрицательного числа –

3 является невыполнимой операцией. Используя введённый символ i = −1 , получим ещё два сопряжённых комплексных корня

Перейдём к определению операций над комплексными числами.

Суммой комплексных чисел z1 = x1 + iy1 и z2 = x2 + iy2 называется комплексное число

Произведением комплексных чисел z1 = x1 + iy1 и z2 = x2 + iy2 называется ком-

Замечание. Операции сложения и умножения можно выполнять по обычным правилам раскрытия скобок, заменяя i2 на –1.

Операции вычитания и деления определяются как обратные сложению и умножению. В частности, можно найти такое комплексное число z = x + iy, что

z2 z = z1. Действительно, согласно (2), получим систему уравнений для x и y:

Таким образом, частным комплексных чисел z1 = x1 + iy1 и z2 = x2 + iy2 называется комплексное число

Замечание. Результат (3) может быть получен умножением числителя и знаме-

нателя дроби z1 на z2 . z2

Если на плоскости ввести декартову прямоугольную систему координат OXY, то всякому комплексному числу z = x + iy может быть поставлена в соответствие некоторая точка M(x,y) с абсциссой x и ординатой y (рисунок 2). Ось OX называется действительной осью (её точки изображают действительные числа), ось OY –

мнимой осью, вся плоскость – комплексной плоскостью.

14

Множество точек на координатной плоскости с абсциссой x и ординатой y будем обозначать символом R2 . Итак, R2 ={( x, y ) : x, y R} .

Запись z = x + iy называется алгебраической формой комплексного числа z. Рассмотрим другие формы записи комплексного числа.

Для этого рассмотрим полярные координаты, совмещая полярную ось с положительной полуосью OX, а полюс с началом координат. Тогда если обозначить

через r полярный радиус, а через ϕ полярный угол точки z (рисунок 2), то будем иметь:

z = r(cosϕ + i sinϕ) – тригонометрическая форма записи.

Полярный радиус r равен модулю числа z, а

угол ϕ называют его аргументом .

В то время как модуль комплексного числа определяется однозначно: r = z = x2 + y2 ≥0 , аргумент определён лишь с точностью до слагаемого, кратного 2π:

cosϕ = | xz | , sinϕ = | zy | , | z |≠ 0 .

Рисунок 2 Значение ϕ, удовлетворяющее условию 0 ≤ ϕ < 2π, называют главным значением

аргумента и обозначается символом arg z.

Пусть z1 = r1(cosϕ1 + i sinϕ1), z2 = r2(cosϕ2 + i sinϕ2). Вычислим произведе-

ние:

Полученный результат позволяет ввести еще одну форму записи комплексных чисел – показательную:

z = r(cosϕ + i sinϕ) = reiϕ .

Здесь новое обозначение комплексного числа обладает известным свойством экс- поненты: eiϕ1 eiϕ2 = ei( ϕ1 +ϕ2 ) .

Пример 4. Записать в тригонометрической и показательной формах число

15

Рассмотрим важные операции над комплексными числами: возведение в целую степень и извлечение корня.

Применяя формулу (4) к произведению n сомножителей z z ... z = zn, полу-

чим формулу Муавра:

Легко проверить, что формула Муавра справедлива и при отрицательных целых n, т.е. для n Z.

Научимся извлекать корни n-й степени из комплексных чисел, т.е. решать уравнение zn = w, где z = |z| (cosϕ + i sinϕ), w = |w| (cosα + i sinα).

Для этого подставим эти выражения в рассмотренное уравнение:

|z|n (cosnϕ + i sinnϕ) = |w| (cosα + i sinα).

Из равенства комплексных чисел следует, что|z|n = |w|, nϕ = α + 2kπ, k Z.

Здесь выписаны n различных значений zk, которые получаются, например, при k = 0, 1, ..., n–1.

16

Получили три различных значения. Подстановка других значений k не дает новых решений. •

Между комплексными числами z1 и z2 определяется расстояние – это действительное число |z1 – z2|. Такое определение хорошо согласуется с геометрической

– хорошо известная формула для расстояния между точками (x1, y1) и (x2, y2).

Множество Uε ( z0 ) ={z C : | z − z0 |<ε} называется ε – окрестностью точ-

ки z0.

1.4Операции над множествами

Вкаждой конкретной задаче множества, имеющие к ней отношения, лежат обычно в некотором так называемом универсальном множестве. Например, если речь идет только о птицах и кому-то захотелось высказаться о многих видах птиц, то не следует упоминать о лошадях и разумно считать таким универсальным множеством множество всех птиц. Если же разговор ведут о собаках, кошках, птицах, то универсальным множеством удобнее считать множество всех животных.

Для числовых множеств в качестве универсального множества можно взять

множество комплексных чисел C или множество действительных чисел R, исходя из характера рассматриваемых задач.

Будем рассматривать множества, являющиеся подмножествами некоторого универсального множества E. Рассмотрим основные операции над множествами.

Объединением (суммой) двух множеств А и В называется множество, обозначаемое A U B ,состоящее из элементов, принадлежащих хотя бы одному из этих множеств:

A U B = {x E : x A или x B}.

Пересечением (произведением) двух множеств А и В, называется множество, обозначаемое A I B ,состоящее из элементов, которые принадлежат одновременно и А, и В:

A I B = {x E : x A и x B}.

Если A I B = , то множества А и В называются непересекающимися.

Разностью двух множеств А и В называется множество, обозначаемое А \ В,

исостоящее из тех элементов множества А, которые не принадлежат В:

А\ В = {x E : x A и x B}.

17

Разность E \ A обозначается символом А и называется дополнением множества A (до множества E):

А = E \ A = {x E: x А}.

Пример 7. Даны множества А = {1, 2, 3, 9}, В{1, 2, 5, 7}, Е = {1, 2, ... , 10}.

Найти A U B , A I B , А \ В, В \ А, А, B .

• A U B = {1, 2, 3, 5, 7, 9}, A I B = {1, 2}, А \ В = {3, 9}, В \ А = {5, 7}, А = {4, 5, 6, 7, 8, 10}, B = {3, 4, 6, 8, 9, 10} . •

Замечания.

1)Операции объединения и пересечения естественным образом обобщаются на случай произвольного числа множеств.

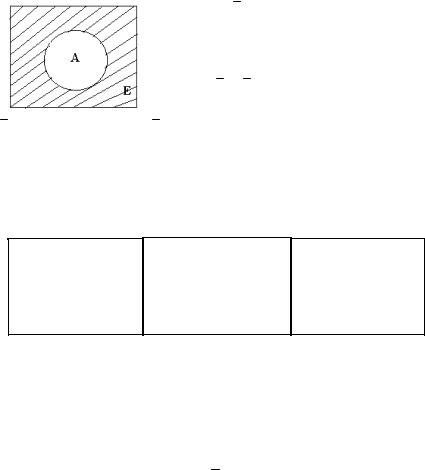
2)Наглядно операции над множествами можно иллюстрировать, изображая множества в виде кругов, называемых кругами Эйлера (рисунок 3). Множества, полученные в результате этих операций, отмечены штриховкой.

А

Рисунок 3

Задача. Пусть множества A и В имеют конечное число элементов n(A) и n(B) соответственно. Найти число элементов n( A U B ) множества A U B .

• Пусть множества A и В не пересекаются, т.е. n( A I B ) = 0 . Их объединение

получается добавлением к элементам одного множества всех элементов другого множества, поэтому n( A U B ) = n( A ) + n( B ).

Если же пересечение множеств A и В не пусто, то число их общих элементов равно n( A I B ) . Объединение этих множеств образуется добавлением к элементам множества A всех тех элементов множества В, которые не входят в A. Число

18

Пример 8. Экзамен по математике сдавали 500 абитуриентов, оценку ниже пяти получили 420 человек, а выдержали этот экзамен 460 абитуриентов. Сколько человек получили оценки 3 и 4?

• Пусть А – множество абитуриентов, выдержавших экзамен, В – множество абитуриентов, получивших оценки ниже 5. По условию

n( A ) = 460, n( B ) = 420, n( A U B ) = 500 .

Абитуриенты, получившие оценки 3 и 4, образуют множество A I B . По форму-

ле (7) находим n( A I B ) = n( A ) + n( B ) − n( A U B ) = 460 + 420 − 500 = 380 .

•

2. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

2.1 Высказывания. Операции над высказываниями

Математическая логика, как и теория множеств, составляет основу математики. Предметом изучения математической логики являются высказывания.

Высказыванием называют предложение (утверждение), относительно которого имеет смысл утверждать, что оно истинно или ложно. Каждому высказыванию сопоставляется одно из двух значений истинности, которые будем обозна-

чать буквами И и Л. Сами высказывания обозначаются заглавными латинскими буквами А, В, С, ... .

Запись |A| = И будет означать, что буквой А обозначено истинное высказывание. Примеры высказываний:

1)А : Барнаул является столицей Алтайского края;

2)В : Луна – спутник Земли;

3)С : 3 < 5 ;

4)D : существуют x, y R такие, что x2 + y2 < 0;

5)E : 4 – простое число.

Здесь |A| = |B| = |C| = И, |D| = |E| = Л.

Высказывания могут быть образованы с помощью слов или символов, однако далеко не каждый набор слов или символов является высказыванием. Например, предложения «x2 + y2», «Сколько в небе звезд?» высказываниями не являются, так как судить об их истинности или ложности невозможно.

В логике вводятся операции над высказываниями. Соединяя простые высказы-

вания словами «и», «или», «не», «если ... , то …», «тогда и только тогда, когда

...», мы можем получить более сложные высказывания, которые определяют нашу речь. В математике эти слова называют логическими связками. Истинность или ложность сложного высказывания полностью определяется, во-первых, тем, какие логические связки используются для образования сложного высказывания, и, вовторых, тем, какие из простых высказываний, образующих сложное, истинны и какие ложны.

Дадим определения основных логических операций.

19

1) Конъюнкцией A B высказываний А и В называют высказывание, которое истинно тогда и только тогда, когда оба высказывания истинны. Логический символ конъюнкции соответствует союзу «и» , т.е. «и А, и В».

2) Дизъюнкцией A B высказываний А и В называют высказывание, которое ложно тогда и только тогда, когда оба высказывания ложны(а истинно, когда хотя бы одно из них (А или В) истинно). Логический символ дизъюнкции соответствует неразделительному «или», т.е. «или А, или В, или и то и другое».

3)Импликацией А В высказываний А и В называют высказывание, которое ложно тогда и только тогда, когда А истинно, а В – ложно. Читать формулу А

В можно так: «из А следует В», «если А, то В», «А влечет В». Высказывание

А называется посылкой, В – заключением импликации.

4)Эквиваленцией А В высказываний А и В называют высказывание, которое истинно тогда и только тогда, когда оба высказывания А и В истинны, или оба высказывания ложны. При чтении используются обороты: «А эквивалентно В», «А тогда и только тогда, когда В», «А необходимо и достаточно для В».

5)Отрицанием высказывания А называется высказывание А, которое истинно, если А ложно, и ложно, когда А истинно. Читается как «не А», «отрицание А».

Определения логических операций можно дать в виде таблиц истинности:

АА

ИЛ

ЛИ

Пример 9. Определить истинность следующих высказываний:

А : Катунь – приток Оби, а Обь впадает в Чёрное море;

В : Равенство lg10 = 2 эквивалентно равенству 2 × 2 = 5;

С : (9 < 12) (9 = 12); D : (9 < 12) (9 = 12).

• Высказывание А есть конъюнкция двух высказываний: А1 : Катунь – при-

ток Оби и А2 : Обь впадает в Черное море. Высказывание А2 ложное, поэтому |A| = Л.

Высказывание В есть эквиваленция двух ложных высказываний, следовательно

|В| = И.

|С| = И как дизъюнкция двух высказываний, одно из которых истинно. |D| = Л как конъюнкция двух высказываний, одно из которых ложно. •

20