
Matematika_Zaytsev_ch2
.pdf
z//yy= 10x2, |
z///xxx= 24x, |
z///xxy= 20y, z///xyx= 20y, z///xyy= 20x, z///yxx= 20y, |
z///yxy= 20x, |
z///yyx= 20x, |
z///yyy= 0. ● |
Сравнивая между собой значения смешанных производных в примере 8, видим, что
z//xy= z//yx , |
z///xxy= z///xyx= z///yxx , |
z///xyy= z///yxy= z///yyx , |
т.е. смешанные частные производные данной функции, отличающиеся лишь последовательностью произведённых дифференцирований, совпадают друг с другом. Это подмеченное на конкретном примере свойство имеет место для широкого класса функций, что подтверждается следующей теоремой.
Теорема 3. Если функция z = f(x, y) имеет все частные производные до n-го порядка включительно и эти производные непрерывны, то смешанные производные порядка m ≤ n, отличающиеся друг от друга лишь последовательностью дифференцирований, совпадают между собой.
Доказательство этой теоремы довольно громоздкое и в данном пособии не приводится.
Итак, любую частную производную порядка m (если она непрерывна) можно получить, выполнив вначале все необходимые дифференцирования по x, а затем все положенные дифференцирования по y, т.е. любая частная производная порядка
∂m z
m такой функции может быть записана в виде: ∂xk ∂ym-k , где k – одно из чисел
0, 1, 2, ..., m.
Отсюда следует, что число различных частных производных порядка m у этой функции равно m+1, а не 2m, как было указано раньше.
2.4 Дифференциал функции
Напомним, что если функция z = f(x, y) дифференцируема в точке M(x, y), то её полное приращение в этой точке может быть представлено в виде
∆f(M) = fx/ (M)∆x + f y/ (M)∆y + α1∆x + α2∆y,
где α1 и α2 – б.м. при ∆x→0, ∆y→0.
Главная, линейная относительно приращений ∆x и ∆y, часть полного приращения функции z = f(x, y) в точке M(x, y), т.е. fx/ (M)∆x + f y/ (M)∆y, называется её
дифференциалом в этой точке и обозначается df(x, y), df(M) или dz. |
|
Итак, |
|
df(M) = fx/ (M)∆x + f y/ (M)∆y. |
(5) |
Полагая, в частности, z = f(x, y) ≡ x, получаем dz = dx = 1·∆x + 0·∆y = ∆x, т.е dx = ∆x. Аналогично, полагая z = y, получаем, что dy = ∆y.
Итак, дифференциалы независимых переменных совпадают с приращениями этих переменных, и мы можем записать дифференциал функции z = f(x,y) в виде
df(x, y) = fx/ (x, y)dx + f y/ (x, y)dy. |
(6) |
177 |
|

Пример 7. Записать дифференциал функции z = xy3 в точке A(1; 2).
● fx/ (M)= y3, f y/ (M) = 3xy2, fx/ (A )= 8, f y/ (A) = 12, df(A) = 8∆x + 12∆y. ●
Из определения дифференциала следует, что ∆z − dz = α1∆x + α2∆y, т.е. разность между полным приращением и дифференциалом функции в точке M(x, y) есть б.м. более высокого порядка, чем ∆x и ∆y (или, что то же, чем
r = ( ∆x )2 + ( ∆y )2 ). Поэтому, ∆z = dz + o( (∆x)2 + (∆y)2 ) , а это равно-
сильно приближённому равенству (при достаточно малых ∆x и ∆y)
f(x+∆x, y +∆y) ≈ f(x, y) + fx/ (x, y)∆x + f y/ (x, y)∆y. |
(7) |
Последнюю формулу используют в приближённых вычислениях.
Пример 8. Вычислить приближённое значение (1,08)3,96.
● Заметим, что (1,08)3,96 есть частное значение функции f(x, y) = xy в точке M1(1,08; 3,96). Возьмём близкую к точке M1 точку M0(1; 4), в которой функцию и частные производные легко вычислить:
f(M0)=14=1, fx/ =yxy –1 fx/ (M0)=4·13=4, f y/ =xylnx f y/ (M0)=14ln1=0.
Т. к. ∆x=1,08 − 1= 0,08, |
∆y=3,96 − 4 = − 0,04, то, согласно (7) в точке M0 , полу- |
чим (1,08)3,96 ≈ f(M0 )+ |
fx/ (M0)∆x + f y/ (M0)∆y = 1+4·0,08 + 0·(− 0,04)=1,32. ● |
Итак, для дифференцируемой функции z = f(x, y) в точке M(x, y) можно вычислить её дифференциал df(M) = fx/ (M)dx + f y/ (M)dy (будем называть его
дифференциалом первого порядка). Он зависит от значений x, y, dx, dy, т.е. являет-
ся функцией 4-х переменных. Закрепляя dx и dy (считая их постоянными), получаем функцию двух переменных x и y.
Дифференциал от этой функции, т.е. d(df), если он существует, называется
дифференциалом второго порядка функции z = f(M) в точке M(x, y). Обозначает-
ся d2f(M) или d2z.
Аналогично определяются дифференциалы третьего, четвёртого, ..., n-го по-
рядков. При этом
d n f ( M ) = d (d n-1 f ( M )) .
Если функция z = f(x, y) в точке M(x, y) имеет непрерывные частные производные до n-го порядка включительно, то все дифференциалы до n-го порядка включительно существуют в этой точке. Вычисляя их по известным правилам, по-
лучим (считая, что dx и dy – постоянные): |
|
|
|
|
|
|||
dz = fx′dx + f y′dy; d 2 z = d( fx′dx + f y′dy ) = dfx′dx + df y′dy = |
|
|
||||||
′′ |
′′ |
′′ |
′′ |
′′ |
2 |
′′ |
′′ |
2 |
= ( fxxdx + |
fxydy )dx |
+ ( f yxdx + |
f yydy )dy = |
fxx ( dx ) |
|
+ 2 fxydxdy + |
f yy ( dy ) |
; |
|
|
|
178 |
|
|
|
|
|
d 3 z = d [ fxx′′ ( dx )2 + 2 fxy′′ dxdy + f yy′′ ( dy )2 ] =
= |
′′′ |
3 |
′′′ |
2 |
′′′ |
2 |
+ |
′′′ |
3 |
|
fxxx ( dx ) |
+ 3 fxxy ( dx ) |
dy + 3 fxyydx( dy ) |
f yyy ( dy ) |
и т. д. |
||||||
Пример 9. Записать d2z, если z = exy.
• z′x = e xy y, z′y = e xy x, z′′xx = e xy y2 , z′′xy = e xy xy + e xy , z′′yy = e xy x2 .
Поэтому,
d 2 z = e xy y2 ( dx )2 + 2( e xy xy + e xy )dxdy + e xy x2 ( dy )2 = • = e xy [ y2 ( dx )2 + 2( xy + 1 )dxdy + x2 ( dy )2 ].
2.5 Дифференцирование сложных функций
Пусть z = f(x, y) – функция двух переменных, каждая из которых является функцией независимой переменной t: x = x(t), y = y(t). Тогда z = f(x(t), y(t)) – сложная функция одной независимой переменной t, переменные x и y будут для неё промежуточными переменными.
Теорема 4. Если функции x(t) и y(t) дифференцируемы в точке t, а функция z = f(x, y) дифференцируема в точке M(x(t), y(t)), то сложная функция
z = f(x(t), y(t)) также дифференцируема в точке t, причём
dz |
= |
∂z |
|
dx |
+ |
∂z |
|
dy |
. |
(8) |
dt |
∂x |
dt |
∂y |
|
||||||
|
|
|
|
dt |
|
|||||
Доказательство. Дадим переменной t произвольное приращение ∆t, тогда функции x(t) и y(t) получат соответственно приращения ∆x и ∆y, а функция
z = f(x, y) – приращение ∆z = f(x +∆x, y +∆y) – f(x, y). Так как функция z = f(x, y)
дифференцируема в точке M(x, y), где x = x(t), y = y(t), то имеем |
|
||||||||||
∆z = f x′( M )∆x + f y′( M )∆y +α1∆x +α2∆y, где α1 |
и α2 – б. м. при ∆x→ 0, |
||||||||||
∆y→ 0. Разделив на ∆t, получим |
|
|
|
|
|
|
|
|
|
|
|
∆z = fx′( M ) |
∆x |
+ f y′( M ) ∆y +α1 |
∆x +α2 ∆y . |
(*) |
|||||||
∆t |
∆t |
|
|
|
∆t |
∆t |
∆t |
|
|||
По условию теоремы lim |
∆x |
= |
dx |
, |
lim |
∆y = |
dy |
|
в точке t. Из дифференци- |
||
∆t |
|
|
|||||||||
∆t →0 |
|
dt |
∆t→0 |
∆t |
dt |
|
|
||||
руемости функций x(t) и y(t) следует их непрерывность, поэтому, при ∆t→ 0 име-
ем ∆x→ 0 и ∆y→ 0, а, значит, и α1→ 0, α2→ 0.
Таким образом, существует предел правой части равенства (*), а, следователь-
но, существует предел и левой части lim |
∆z |
= |
dz |
|
и справедлива формула (8). |
|||
∆t |
dt |
|||||||
|
|
∆t →0 |
|
|
||||
Пример 10. Найти |
dz |
, если z = xy, где x = lnt, |
y = sin2t. |
|||||
dt |
||||||||
|
|
|
|
|
|
|
||
|
|
179 |
|
|
|
|
||

•По формуле (8) имеем:
dzdt = ( x y )′x (ln t )t′ + ( x y )′y (sin2 t )t′ = yx y−1 1t + x y ln x 2 sin t cos t .
Результат можно оставить в таком виде, а можно заменить x и y соответственно
2 |
|
dz |
|
2 |
|
sin2 t −1 |
|
1 |
|
sin2 t |
|
на lnt и sin |
t, и тогда |
|
= sin |
|
t(ln t ) |
|
|
|
+ (ln t ) |
|
ln(ln t )sin 2t .• |
dt |
|
|
t |
|
|||||||
|
|
|
|
|
|
|
|
|
|
Следствие. Если z = f(x, y), где y = y(x), то z = f(x, y(x)) – сложная функция переменной x. На основании формулы (8), в которой роль t играет теперь x, полу-
чим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dz |
= |
∂ z |
|
dx |
+ |
∂ z |
|
dy |
= |
∂ z |
+ |
∂ z |
|
dy |
. |
|
(9) |
|||
|
dx |
∂ x |
|
∂ y |
dx |
∂ x |
∂ y |
|
|
||||||||||||
|
|
|
dx |
|
|
|
|
|
dx |
|
|
||||||||||
В формуле (9) участвует частная производная |
|
∂ z |
функции z = f(x, y) (она |
||||||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ x |
|
|
|
dz |
|
|||
вычисляется при закрепленном значении y) |
и полная производная |
сложной |
|||||||||||||||||||
dx |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
функции z = f(x, y(x)) – зависящей от x явным образом и через величину y.
|
|
|
∂ z |
|
dz |
xy |
|
|
|
|
|
|
|
|
|
|
|||
Пример 11. Найти |
|
и |
|
, если z = e , где y = tgx. |
|
|
|
|
|
|
|||||||||
∂ x |
dx |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂ z |
|
|
|
|
|
xy |
∂ z |
xy |
• Вначале вычислим частную производную |
|
|
функции z = e |
: |
|
= e y. |
|||||||||||||
|
∂ x |
∂ x |
|||||||||||||||||
По формуле (9) получим полную производную: |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
dz |
|
|
xy |
|
|
|
xy |
′ |
xy |
|
x |
|
|
|
|
|
|
|
|
|
= e |
|
y + e |
|
x ( tgx ) = e |
|
y + |
|
|
. |
• |
|
|
|
||||
|
dx |
|
|
|
cos2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||
Рассмотрим теперь общий случай. Пусть z = f(x, y) – функция двух переменных x и y, которые, в свою очередь, зависят от двух или большего числа независимых переменных. Например, пусть x = x(t1, t2), y = y(t1, t2). Тогда функция
z = f(x(t1, t2), y(t1, t2)) является сложной функцией независимых переменных t1 и t2, а переменные x и y – промежуточные.
Теорема 5. Если функции x(t1, t2), y(t1, t2) дифференцируемы в точке (t1, t2), а функция z = f(x, y) дифференцируема в точке (x(t1, t2), y(t1, t2)), то сложная функция z = f(x(t1, t2), y(t1, t2)) дифференцируема в точке (t1, t2), причём
∂ z |
= |
∂ z |
|
∂ x |
+ |
∂ z |
|
∂ y |
, |
∂ z |
= |
∂ z |
|
∂ x |
+ |
∂ z |
|
∂ y |
. |
(10) |
∂ t1 |
|
|
|
|
∂ t2 |
|
|
|
|
|||||||||||
|
∂ x |
∂ t1 |
∂ y |
∂ t1 |
|
∂ x |
∂ t2 |
∂ y |
∂ t2 |
|
||||||||||
Доказательство этой теоремы в данном пособии не приводится. Формулы (10) получаются как следствие формулы (8), так как при нахождении частных производных фиксируется значение одной из переменных t1, t2.
180

Пример 12. Найти ∂∂ uz и ∂∂ vz функции z = x2lny, если x = uv , y = u2 + v2.
• В этом примере независимые переменные имеют другое обозначение: t1 = u, t2 = v. Имеем, согласно (10):
∂ z |
|
|
2 |
|
|
′ |
v |
′ |
|
2 |
|
′ |
(u |
2 |
|
|
2 |
) |
|
′ |
|
|
|
|
v |
|
|
|
|
x2 |
|
|
||||||
|
= ( x |
|
ln y )x |
|
|
|
|
+ ( x |
|
ln y )y |
|
+ v |
|
|
|
= 2 x ln y |
− |
|
|
|
+ |
|
|
|
2u ; |
|||||||||||||
∂ u |
|
|
|
|
|
u |
u |
2 |
|
y |
||||||||||||||||||||||||||||
|
|
|
|
|
|
u u |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∂ z |
|
|
|
2 |
′ |
|
v |
|
2 |
′ |
|
|
2 |
|
|
|
2 |
|
′ |
|
|
1 |
|
|
|
x2 |
|
|
|
|||||||||
|
|
= ( x |
|
ln y )x |
|
|
+ ( x |
|
ln y )y (u |
|
+ v |
|
|
) |
|
= 2 x ln y |
|
|
+ |
|
|
|
|
2v |
. • |
|||||||||||||
∂ v |
|
|
|
|
|
|
|
|
|
|
y |
|||||||||||||||||||||||||||
|
|
|
|
|
|
u v |
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
u |
|
|
|
|
|
|
|
|||||||||
Замечание. Формулы (10) можно обобщить на случай большего числа как промежуточных, так и независимых переменных.
Пусть z = f(x1, ... , xn) – дифференцируемая функция n переменных x1, ... , xn, причем эти переменные, в свою очередь, являются дифференцируемыми функция-
ми m независимых переменных t1, ... , tm, т. е. xi = xi(t1, ... , tm), |
i = 1, ... , n. Тогда |
||||||||||||||||||
|
∂ z |
= |
∂ z |
|
|
∂ x1 + |
|
∂ z |
∂ x2 + ...+ |
|
∂ z |
∂ xn , |
j = 1,...,m. (11) |
||||||
|
∂ t j |
∂ x1 |
|
∂ x2 |
∂ xn |
||||||||||||||
|
|
|
∂ t j |
|
|
∂ t j |
|
∂ t j |
|
||||||||||
При n = 2 |
(x1 = x, |
|
x2 = y) и m = 1 (t1 = t) из (11) получится формула (8), так |
||||||||||||||||
как в этом случае ∂ z |
= |
dz |
, |
∂ x = |
dx |
, |
∂ y = |
dy |
. |
|
|
||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
∂ t |
|
|
dt |
|
∂ t |
|
dt |
∂ t |
|
dt |
|
|
||||
При n = 2 (x1 = x, |
|
x2 = y) и m = 2 имеем (10). |
|
|
|||||||||||||||
Используя правило дифференцирования сложной функции, легко показать, что дифференциал функции нескольких переменных обладает свойством инвариант-
ности, т. е. имеет одинаковую форму записи как в случае, когда аргументы этой функции являются независимыми переменными, так и в случае, когда они являются функциями других переменных.
Действительно, сложную функцию z = f(x1, ... , xn), где xi = xi(t1, ... ,tm), можно записать в виде z = f(x1(t1, ... ,tm), …, xn(t1, ... ,tm)) ≡ F(t1, ... ,tm). Найдем выра-
жение дифференциала этой функции, используя (11):
|
|
|
∂ F |
|
|
|
|
∂ F |
|
|
|
∂ z |
|
∂ x |
1 + ...+ |
∂ z |
|
∂ x |
n |
|
|
|
||||||||
dz |
= |
|
|
|
dt1 + ...+ |
|
|
|
dtm = |
|
|
|
|
|
|
|
dt1 |
+ ...+ |
|
|||||||||||
∂ t1 |
|
∂ tm |
∂ x1 |
|
|
∂ xn |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂ t1 |
|
|
|
|
∂ t1 |
|
|
|
|
||||||||||
|
|
∂ z |
|
|
|
|
|
|
∂ z |
|
|
|
|
|
∂ z |
|
|
|
|
|
|
|
|
|
|
|
||||
+ |
|
|
∂ x1 + ... |
+ |
|
∂ xn dtm |
= |
|
|
∂ x1 dt1 |
+ ...+ |
∂ x1 |
dtm |
+ |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
∂ x1 |
∂ tm |
|
|
∂ xn |
∂ tm |
|
|
∂ x1 |
∂ t1 |
|
|
|
|
∂ tm |
|
|
||||||||||||
+...+ |
|
∂ z |
|
|
∂ xn dt1 + ...+ |
∂ xn dtm |
|
= |
∂ z |
|
dx1 + ...+ |
∂ z |
|
dxn . |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
∂ x1 |
|
∂ xn |
|
|
||||||||||||||||||||||
|
|
|
|
∂ xn |
∂ t1 |
|
|
|
|
|
∂ tm |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Это и доказывает утверждение.
181
2.6 Дифференцирование неявной функции
Пусть дано уравнение |
|
F(x1 , ... , xn , z) = 0, |
(**) |
связывающее n+1 величин, одну из которых, например z, мы будем считать неявной функцией остальных.
При определенных условиях, налагаемых на функцию F, равенство (**) действительно задает функцию z = z (x1 , …, xn). Приведем формулировку (без доказательства) теоремы о существовании неявной функции.
Теорема 6 (о существовании неявной функции).
Пусть выполнены условия:
1)уравнение (**) обращается в тождество в точке M ( x1 ,..., xn ,z ) ;
2)в некоторой окрестности точки M функция F непрерывна и имеет частные производные, причем Fz′( M ) ≠ 0 .
Тогда уравнение (**) в рассматриваемой окрестности точки M имеет единственное решение z = f(x1 , ..., xn) (т. е. уравнение (**) определяет неявную функцию z), при этом функция f(x1 , ..., xn) – дифференцируема.
Предполагая условия теоремы 6 выполненными, найдём значения для производных неявной функции z аргументов x1 , ..., xn.
Подставим в уравнение (**) решение z = f(x1 , ..., xn), тогда уравнение обратится в тождество F(x1 , ..., xn , f(x1 , ..., xn)) ≡ 0. Следовательно, дифференциал сложной функции F(x1 , ..., xn , z), где z = f(x1 , ..., xn), равен нулю. Используя свойство инвариантности, выписываем дифференциал и приравниваем его нулю:
|
∂ F |
dx1 + ...+ |
∂ F |
dxn + ∂ F dz = 0 . Отсюда, так как |
∂ F |
≠ 0 , имеем: |
|
|
||||||||||||||||||||||||||
|
|
∂ x n |
∂ z |
|
|
|||||||||||||||||||||||||||||
|
∂ x 1 |
|
|
|
|
|
|
|
|
∂ z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
∂F |
|
|
|
|
|
∂F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∂ x |
|
|
|
|
∂ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z |
|
∂z |
|
|||||||||
dz = − |
|
|
1 |
|
dx + ...+ − |
|
|
|
n |
|
dx . С другой стороны, |
dz = |
|
dx +...+ |
|
dx . |
||||||||||||||||||
|
|
∂F |
|
|
1 |
|
|
|
∂F |
|
n |
|
|
|
|
|
|
|
|
|
|
∂x1 |
1 |
∂xn |
n |
|||||||||
|
|
∂ z |
|
|
|
|
|
|
|
∂ z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Сравнивая эти выражения, получим: |
|
|
|
|
|
∂ F |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
∂ z |
|
= − |
|
∂ x 1 |
, |
... , |
|
∂ z |
= − |
∂ x n |
|
. |
|
|
|
|
(12) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
∂ F |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
∂ x 1 |
|
|
|
|
|
∂ x n |
|
∂ F |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
∂ z |
|
|
|
|
|
∂ z |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Отметим два частных случая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1) Пусть F(x, y) = 0; |
y = y(x), тогда |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
|
= − |
Fx′ |
. |
|
|
|
|
|
|
|
|
|
(13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fy′ |
|
|
|
|
|
|
|
|
|
|
||||
182

Формула (13) обычно используется вместо довольно громоздкого правила дифференцирования неявной функции одной независимой переменной.
2) Пусть F(x, y, z) = 0; z = (x, y). В этом случае
∂z |
|
F ′ |
|
∂z |
|
Fy′ |
|
|
|
|
= − |
x |
, |
|
= − |
|
. |
(14) |
|
∂x |
Fz′ |
∂y |
Fz′ |
||||||
|
|
|
|
|
Пример 13. Найти производную неявной функции y(x), заданной уравнением x4 + y + exy = 0, в точке M(0; −1).
• Согласно (13), имеем: |
dy |
= − |
||||||
|
||||||||
|
|
|
|
|
|
dx |
||
|
|
|
|
|
||||
Поэтому |
dy |
|
|
= − |
0 + 1 |
( −1 ) |
||
dx |
y=−1 |
1 + |
1 0 |
|||||
|
|
|
x=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( x |
4 |
+ y + e |
xy |
′ |
|
4 x |
3 |
+ e |
xy |
y |
|
||
|
|
)x |
= − |
|
|
|
. |
||||||
( x |
4 |
+ y + e |
xy |
′ |
1 + e |
xy |
x |
|
|||||
|
|
|
|||||||||||
|
|
)y |
|
|
|
|
|
||||||
= 1.•
Пример 14. Найти частные производные неявной функции z(x, y), заданной уравнением x2 + y2 + z2 = z.
• Данное уравнение запишем в виде x2 + y2 + z2− z = 0, поэтому функция |
|
|||||||||
F(x,y,z) = x2+ y2+ z2− z. По формуле (14) имеем: |
∂ z |
= − |
2x |
|
, |
∂ z |
= − |
2 y |
. • |
|
∂ x |
2z − |
1 |
∂ y |
2z −1 |
|
|||||
3. ПРИЛОЖЕНИЯ ЧАСТНЫХ ПРОИЗВОДНЫХ
3.1 Формула Тейлора
Аналогично функции одной переменной функцию нескольких переменных при определенных условиях можно представить в виде суммы многочлена и некоторого остаточного члена.
Для упрощения записи ограничимся случаем функции двух переменных. Теорема 7 (формула Тейлора с остаточным членом в форме Лагранжа).
Пусть функция z = f(x, y) непрерывна вместе со всеми частными производными до (n+1) - го порядка включительно в некоторой окрестности точки M0(x0, y0) и пусть точка M(x0 + ∆x, y0 + ∆y) лежит в этой окрестности. Тогда приращение ∆f(M0) = f(M) – f(M0) этой функции в точке M0 можно представить в виде фор-
мулы Тейлора для функции z = f(x, y): |
|
|
|
|
|
|
|
|
|
|
|
|
||||
∆ f ( M |
0 |
) = f ( M ) − f ( M |
0 |
) = df ( M |
0 |
) + |
d 2 f ( M |
0 |
) |
+ ...+ |
d n f ( M |
0 |
) |
+ r |
, (15) |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2! |
|
|
|
n! |
|
|
|
n |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где rn = dn+1 f ( M1 ) – остаточный член в форме Лагранжа, а
( n +1)!
M1(x0 + t ∆x, y0 + t ∆y), t (0; 1) – промежуточная точка на прямолинейном отрезке, соединяющем точки M0 и M.
183
Доказательство. Уравнение отрезка M0M можно записать в параметрической форме в виде: x = x0 + s ∆x, y = y0 + s ∆y, (s [0; 1]). Тогда вдоль этого отрезка функция z = f(x, y) будет функцией одной независимой переменной s:
f(x, y) = f(x0 + s ∆x, y0 + s ∆y) = F(s).
Ясно, что |
|
∆f(M0) = f(x0 + ∆x, y0 + ∆y) – f(x0, y0) = F(1) – F(0) = ∆F(0). |
(*) |
Применяя формулу Маклорена к функции одной переменной F(s) и полагая s=1, получим
∆F( 0 ) = F( 1 ) − F( 0 ) = |
F′( 0 ) |
+ |
F′′( 0 ) |
+ ...+ |
F( n )( 0 ) |
+ |
F( n+1 ) ( t ) |
, t (0;1). (**) |
||||
1! |
|
2! |
|
n! |
|
( n + 1 )! |
|
|||||
|
|
|
|
|
|
|
||||||
Вычислим производные функции F(s) через f(x,y), используя правила дифференцирования сложной функции:
F′( s ) = fx′( M ) ∆x + fy′( M ) ∆y =df ( M ) F′(0 ) =df ( M0 );
F′′( s ) =( fxx′′( M ) ∆x + fyx′′( M ) ∆y )∆x +( fxy′′( M ) ∆x + fyy′′( M ) ∆y )∆y =
=fxx′′( M )( ∆x )2 + 2 fxy′′( M )∆x∆y + fyy′′( M )( ∆y )2 =d2 f ( M ) F′′(0 ) =d2 f ( M0 ).
Продолжая этот процесс, получим:
F'''(0) = d3f(M0); … F(n)(0) = dnf(M0).
В силу этого из соотношений (*) и (**) имеем (15). Теорема доказана.
Из определения дифференциала (n+1) - го порядка функции двух переменных
следует, что остаточный член r |
= |
d n+1 |
f ( M |
1 |
) |
и величина |
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
n |
|
|
( n + 1 )! |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
M0 M |
|
n+1 = ( ( ∆x )2 + ( ∆y )2 )n+1 |
являются б.м. одинакового порядка малости |
||||||||||||
|
|
|||||||||||||||
при ∆x→ 0, ∆y→ 0 (или, что тоже, при M→ M0), т. е. |
|
|
||||||||||||||
|
|
|
rn = O ( |
|
M |
0 M |
n+1 |
|
( |
|
( ∆x )2 + ( ∆y )2 ) |
n+1 |
|
|||
|
|
|
|
|
|
) = O |
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если функция f(M) имеет непрерывные частные производные только до n-го порядка включительно, то остаточный член можно записать в форме Пеано:
rn = о( M0 M n ) .
Отметим, что формула Тейлора для функции двух переменных напоминает формулу Тейлора для функции одной переменной.
Для случая функции большего числа переменных формула Тейлора имеет аналогичный вид.
184
Замечание.
Из формулы Тейлора при n = 0 получается формула Лагранжа (формула конечных приращений), которая для функции двух переменных z = f(x, y) имеет вид:
∆f(x0, y0) = f(x0 + ∆x, y0 + ∆y) – f(x0, y0) = df(x0 + t ∆x, y0 + t ∆y) =
= fx′( x0 + t ∆x, y0 + t ∆y ) ∆x + f y′( x0 + t ∆x, y0 + t ∆y ) ∆y , t (0; 1).
Из этой формулы следует важный результат: если fx′ = f y′ ≡ 0 , то ∆f ≡ 0, а это означает, что f(x, y) = const.
Пример 15. Функцию f(x, y) = x3 – 2y3 + 3xy разложить по формуле Тейлора в окрестности точки M0(2; 1).
• Имеем f(2; 1) = 12. Вычислим последовательно частные производные данной функции и их значения в точке M0(2; 1):
|
fx′( x, y ) = 3x2 + 3 y, fx′( M0 ) = 15; |
f y′( x, y ) = −6 y2 + 3x, |
f y′( M0 ) = 0; |
|
||||||||||||||
|
|
′′ |
|
|
′′ |
|
|
′′ |
|
|
′′ |
( M0 ) = 3; |
|
|
|
|
||
|
fxx |
( x, y ) = 6 x, fxx ( M0 ) = |
12; fxy ( x, y ) = 3, |
fxy |
|
|
|
|
||||||||||
|
|
′′ |
( x, y ) = −12 y, |
′′ |
0 ) = −12; |
′′′ |
|
= 6 , |
′′′ |
) |
= 6; |
|
|
|||||
|
f yy |
f yy ( M |
fxxx ( x, y ) |
fxxx ( M0 |
|
|
||||||||||||
|
|
′′′ |
|
|
′′′ |
|
) = −12. |
|
|
|
|
|
|
|
|
|
|
|
|
f yyy ( x, y ) = −12, |
f yyy ( M0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Все последующие производные тождественно равны нулю. Запишем диффе- |
|||||||||||||||||
ренциалы данной функции в точке M0, учитывая, что ∆x = x – 2, ∆y = y – 1: |
|
|
||||||||||||||||
df ( M0 ) = fx′( M0 )∆x + f y′( M0 )∆y = 15( x − 2 ); |
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
|
′′ |
2 |
|
|
′′ |
|
|
′′ |
|
|
2 |
|
|
|
|
d |
|
f ( M0 |
) = fxx ( M0 |
)( ∆x ) |
|
+ 2 fxy ( M0 )∆x∆y + |
f yy ( M0 )( ∆y ) |
|
|
= |
|
|
||||||
= 12( x − 2 )2 + 6( x − 2 )( y − 1 ) − 12( y − 1 )2 ; |
|
|
′′′ |
|
|
|
|
|
|
|||||||||
|
3 |
|
|
′′′ |
|
3 |
|
′′′ |
|
2 |
|
|
|
|
|
2 |
|
|
d |
f ( M0 |
) = fxxx ( M0 )( ∆x ) |
+ 3 fxxy ( M0 )( ∆x ) |
∆y + 3 fxyy ( M0 |
|
)∆x( ∆y ) |
+ |
|||||||||||
|
|
|
|
|
||||||||||||||
+f ′′′ ( M )( ∆y )3 = 6( x − 2 )3 − 12( y − 1 )3 .
yyy0
Так как все последующие дифференциалы тождественно равны нулю, то формула Тейлора имеет вид:
x3–2y3+3xy =12+15(x–2)+6(x–2)2+3(x–2)(y–1)–6(y–1)2+(x–2)3–2(y–1)3. •
Формула Тейлора при x0 = 0, y0 = 0 называется формулой Маклорена и может быть записана в виде:
f ( x, y ) = |
f ( 0,0 ) + df ( 0,0 ) + |
d 2 |
f ( 0,0 ) |
+ ...+ |
d n f ( 0,0 ) |
+ r |
, |
(15/) |
|
|
|
|
|
||||||
|
|
|
2! |
|
n! |
n |
|
||
|
|
|
|
|
|
|
|||
где приращения аргументов ∆x и ∆y, входящие в дифференциалы, могут быть заменены на x и y.
185
3.2 Производная по направлению. Градиент
Пусть дана функция z = f(x, y), определённая в некоторой окрестности точки M(x, y), и единичный вектор s = {cosα , cos β } любого направления (cosα и
cosβ – направляющие косинусы вектора s ).
Для определения скорости изменения функции в точке M в направлении, задаваемом вектором s , введём понятие производной по направлению. Для этого проведём через точку M прямую так, чтобы одно из направлений на ней совпадало с
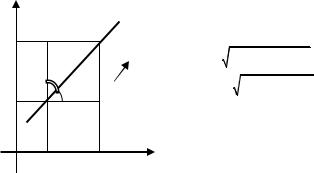
Y |
|
|
|
|
направлением вектора |
s . Возьмём на этой |
|||||
|
|
|
|
|
прямой точку M1(x+∆x, y+∆y) (рисунок 5). |
||||||
y+∆y |
|
M1 |
|
|
Обозначим MM1 = ∆s. Будем считать, что |
||||||
|
|
|
|
|
∆s = |
(∆x)2 +(∆y)2 , |
если |
|
MM |
↑↑ s и |
|
|
|
β |
s |
|
|
|
|
1 |
|
||
|
|
|
∆s=− |
(∆x)2 +(∆y)2 , если |
|
|
↑↓ s . |
||||
y |
M |
α |
|
|
MM1 |
||||||
|
|
|
Рассмотрим приращение функции |
||||||||
|
|
|
|
|
∆z = f(x+∆x, y+∆y) – f(x, y). |
||||||
0 |
x |
x +∆x |
X |
Предел отношения |
∆z при ∆s→ 0 |
||||||
|
|
∆s |
|
|
|
|
|||||
|
Рисунок 5 |
|
|
(M1→ M), если он существует и конечен, |
|||||||
называется производной функции z = f(x, y) |
в точке M(x, y) |
по направлению век- |
|||||||||
тора s |
и обозначается ∂z |
, т. е. lim |
∆z = |
∂z . |
|
|
|
|
|
||
|
|
|
∂s |
∆s →0 |
∆s |
∂s |
|
|
|
|
|
Так как отношение |
∆z |
даёт среднюю скорость изменения функции z на участ- |
|||||||||
|
|
|
∆s |
|
|
|
|
|
|
|
|
ке MM1, то его предел при MM1→ 0, т. е. производная по направлению, есть скорость изменения функции z в точке M в направлении вектора s .
Предположим, что функция z = f(x, y) дифференцируема в точке M(x, y). Тогда можно записать: ∆z = fx′( M )∆x + f y′( M )∆y +α1∆x +α2 ∆y , где α1 и α2 – б. м.
функции при ∆x→ 0, ∆y→ 0 (т. е. ∆s→ 0). Разделив обе части этого равенства на
∆s и учитывая, что |
∆x |
= cosα , |
∆y |
= cos β , получим |
|
∆s |
∆s |
||||
|
|
|
∆∆zs = fx′( M )cosα + f y′( M )cos β +α1 cosα +α2 cos β .
Переходя к пределу в этом равенстве при ∆s→ 0, получим формулу для вычисления производной по направлению
∂ z |
|
= z′x ( M )cosα + z′y ( M )cos β . |
(16) |
|
|||
∂ s |
|
M |
|
|
186 |
|
|
