
Matematika_Zaytsev_ch2
.pdfГлава 6. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
До сих пор мы рассматривали функции одного аргумента (одной переменной), т.е. функции, значения которых зависят от значений одной независимой переменной. Нередки, однако, случаи, когда независимых переменных оказывается несколько.
Так, например, площадь треугольника S зависит от длины основания a и от высоты h, опущенной на это основание. Эта зависимость выражается формулой
S = 0,5ah, которая даёт возможность, зная значения двух независимых переменных a и h, установить соответствующее значение S.
Объём V прямоугольного параллелепипеда с рёбрами, длины которых равны x, y и z, определяется по формуле V = xyz, т.е. зависит от значений трёх независимых переменных x, y и z.
Изучение такого рода зависимостей приводит к понятию функции нескольких переменных, что и будет составлять содержание этой главы.
1. ПОНЯТИЕ ФУНКЦИИ ДВУХ И БОЛЕЕ ПЕРЕМЕННЫХ
1.1 Определения
Уточнение понятия функции в случае нескольких независимых переменных начнём с простейшего случая, когда этих переменных две.
Величина z называется функцией двух независимых переменных x и y, определённой в некоторой области D их изменения, если каждой паре (x, y) их значений из области D по определённому правилу или закону ставится в соответствие единственное значение z.
Область D называется областью определения функции z, а множество всех значений функции z областью значений функции. Переменные x и y называются ар-
гументами функции.
В дальнейшем будем считать, что x, y, z R, т.е. и аргументы, и значения функции – действительные числа.
Запись функции z такова: z = f(x, y), z = g(x, y) и т. п.
Буквы f, g и другие используются для обозначения закона соответствия между независимыми переменными x и y и зависимой переменной z. Иногда и закон соответствия, и результат соответствия обозначают одной буквой, т.е. функцию записывают в виде z = z(x, y).
Если пара (x0, y0) взята из D, то f(x0, y0) означает то частное (числовое) значение функции f(x, y), которое она принимает при x = x0, y = y0.
Способы задания функции двух переменных, как и в случае одной переменной, могут быть различными. Математический анализ изучает преимущественно аналитически заданные функции (т.е. заданные с помощью формулы). Если нет никаких дополнительных условий, то в этом случае за область определения функции будем принимать естественную область определения – область возможности применения формулы.
167
Из определения функции z = f(x, y) следует, что эту функцию можно понимать как функцию точки координатной плоскости OXY, если пару чисел (x, y) изо-
бражать в виде точки M(x, y) на этой плоскости. Тогда возможна запись:
z = f(x, y) = f(M) – функция точки M плоскости. Областью определения функции двух переменных может быть вся плоскость OXY или её часть.
Пример 1. Указать области определения функций:
1) z = x2 + y2; 2) z = 1 − x2 − y2 .
● 1) Область определения этой функции D = {M(x, y): x, y R}, т.е. вся плоскость OXY (ограничений применения данной формулы нет). Ясно, что область значений { z R: z ≥ 0 } – множество всех неотрицательных действительных чисел.
2) Выражение 1 − x2 − y2 определено только при 1− x2 − y2 ≥ 0. Поэтому,
D = {M(x, y): x, y R и x2+y2≤ 1}. Множество таких точек образует единичный круг с центром в начале координат. Область значений функции – отрезок [0; 1]. ●
Как известно, функция одной переменной y = f(x) геометрически иллюстрируется своим графиком – множеством точек {x, f(x)} плоскости OXY, т.е. в общем случае некоторой линией на плоскости.
Подобным образом, функция двух переменных z = f(x, y) геометрически иллюстрируется своим графиком – множеством точек {x, y, f(x, y)} уже в пространстве OXYZ. Это будет, вообще говоря, некоторая поверхность, равенство z = f(x, y)
называется уравнением этой поверхности.
Напомним, что в аналитической геометрии были рассмотрены некоторые поверхности и их уравнения. Так, например, уравнение x − 2y − z + 1 = 0 является уравнением плоскости, т.е. графиком функции z = x − 2y + 1 служит плоскость.
Построение графиков функций двух переменных во многих случаях затруднено. Как было отмечено в главе 3 (пункт 2.4.4) части 1, для изображения поверхности можно применить метод сечений плоскостями z = c, где c – любое число, т.е. плоскостями, параллельными плоскости OXY.
Назовём линией уровня функции z = f(x, y) геометрическое место точек M(x, y) плоскости OXY, в которых функция принимает одно и тоже значение c. Уравнение линии уровня Lc имеет вид: f(x, y) = c. Изменяя значение c, мы будем получать различные линии уровня для данной функции. Вдоль каждой линии уровня Lc
функция z = f(x, y) имеет постоянное числовое значение (z ≡ c).
Если взять числа ci = a + i·h, где a и h – некоторые числа, i = 0, 1, 2, ..., n, то получим ряд линий уровня Lc с уравнениями f(x, y) = ci, по взаимному расположению которых можно получить представление о графике функции z = f(x, y), т.е. о форме поверхности (рисунок 1).
В частности, там, где линии располагаются «гуще», значения функции изменяются быстрее (поверхность, изображающая функцию, идёт «круче»), а там, где линии уровня располагаются «реже», значения функции изменяются медленнее (соответствующая поверхность будет более «пологой»).
168
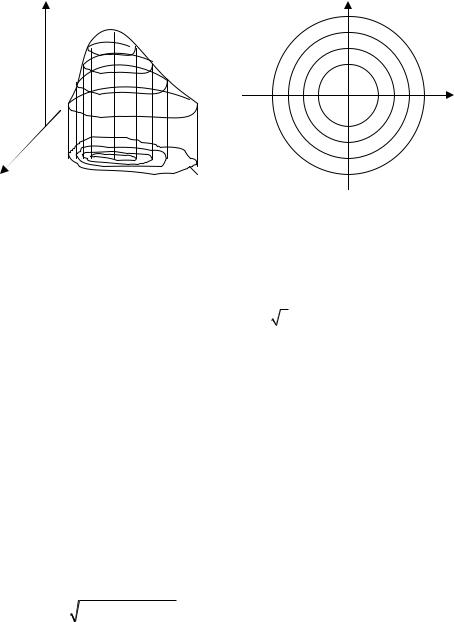
Z |
Y |
L4 |
|
|
|
|
|
z = f(x,y) |
|
L3 |
|
|
|
L2 |
|
|
|
L1 |
X |
|
L0 ● ● ● ● |
||
|
0 |
1 √2 √3 2 |
|
|
|
|
|
 Y
Y
X |
Lc |
Рисунок 1 |
Рисунок 2 |
Выбирая h достаточно малым, можно таким образом получить довольно точное представление о поведении функции.
Пример 2. Для функции z = x2 + y2 записать уравнение линий уровня и изобразить их.
● Уравнение линии уровня Lc: x2 + y2 = c, где 0 ≤ c <+∞. Это окружность с центром в начале координат O(0; 0) и радиусом c . Полагая, например,
c = 0, 1, 2, ... получаем соответствующие линии уровня L0, L1, L2 , ..., сгущающиеся с ростом c. При c = 0 окружность вырождается в точку O(0; 0) (рисунок 2). По виду линии уровня нетрудно заметить, что графиком данной функции является поверхность вращения вокруг оси OZ. Действительно, из аналитической геометрии известно, что уравнение z = x2 + y2 определяет параболоид вращения. ●
Линии уровня часто используются при составлении географических карт (линии уровня – это линии, на которых высота точек земной поверхности над уровнем моря одинакова), при составлении метеорологических карт (линии уровня – линии одинаковых температур (изотермы), линии равного давления (изобары)) и т.д.
Понятие функции u трёх независимых переменных x, y, z даётся аналогично случаю двух переменных.
Функцию u = f(x, y, z), так же как и функцию двух переменных, можно рассматривать как функцию точки M(x, y, z), но уже не на плоскости OXY, а в про-
странстве OXYZ: u = f(x, y, z) = f(M).
Область определения теперь представляет собой всё пространство или его часть. Так, например, функция u = x2 + y2 + z2 определена во всём пространстве, а
функция u = 1 − x2 − y2 − z2 определена только для тех точек пространства,
координаты которых удовлетворяют неравенству 1− x2− y2− z2 ≥ 0, т.е. определена в единичном шаре с центром в начале координат.
Изобразить функцию трёх переменных с помощью графика в трёхмерном пространстве нельзя. Для наглядного изучения функций трёх переменных используют-
169
ся так называемые поверхности уровня функции.
Поверхностью уровня функции u = f(x, y, z) называют геометрическое место точек пространства, в котором функция принимает одно и тоже значение c. Уравнение поверхности уровня: f(x, y, z) = c. Изменяя c, получим различные поверхности уровня. Так, например, у функции u = x2 + y2 + z2 поверхностями уровня будут сферы с уравнением x2 + y2 + z2 = c, где 0 ≤ c < +∞.
Аналогично можно ввести понятие функции произвольного числа n переменных
u= f(x1, x2 , ..., xn).
Вдальнейшем будем подробно рассматривать лишь функции двух переменных,
имея в виду, что перенос полученных определений и полученных результатов на функции трёх и более переменных представляет, как правило, лишь технические трудности.
1.2Понятие предела и непрерывности
Рассмотрим функцию двух переменных z = f(x, y) или, что тоже, z = f(M) –
функцию точки M(x, y). |
M(x, y) стремится к точке M0(x0, y0), если рас- |
|||||
Будем говорить, что точка |
||||||
стояние между этими точками |
MM |
0 |
= |
( x − x |
)2 + ( y − y )2 |
стремится к ну- |
|
|
|
0 |
0 |
|
|
лю, т.е.
M → M0 MM0 → 0 x → x0 и y → y0.
Множество точек M(x, y) таких, что расстояние между точками M и M0(x0, y0)
меньше δ (δ R, δ > 0), называется δ – окрестностью точки |
M0 и обозначается |
||||||
Uδ ( M0 ) . Итак, |
|
|
|
||||
U |
δ |
( M |
0 |
) = { M(x, y): MM0<δ } = { M(x, y): 0 ≤ |
( x − x )2 |
+ ( y − y )2 |
< δ }, |
|
|
|
0 |
0 |
|
||
– это все точки, лежащие внутри круга с центром M0 радиуса δ.
Множество Uδ ( M0 ) \ {M0} называется проколотой δ – окрестностью точки
M0 и обозначается Uδ0 ( M0 ) .
Обобщая данное ранее определение предела функции одной переменной, дадим определение предела функции двух переменных.
Число A называется пределом функции z = f(M) в точке M0, если для любого сколь угодно малого положительного числа ε найдётся другое положительное число δ(ε), такое, что для всех точек M из проколотой δ – окрестности точки
M0 будет выполняться неравенство |f(M) − A|<ε. |
||
Обозначение: lim |
|
f ( M ) = A или lim f ( x, y ) = A . Итак, |
M →M |
|
x→x |
|
0 |
y→ y0 |
|
|
0 |
lim f(x,y)=A: ε>0 |
δ(ε)>0: |
( |
(x−x )2 |
+( y−y )2 |
<δ |
|
f(x,y)−A |
|
<ε |
) |
. (1) |
|
|
||||||||||
x→x0 |
|
0 |
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||
y→y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
170 |
|
|
|
|
|
|
|
|
|
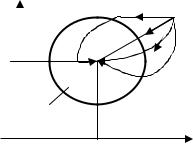
Замечания.
1. Согласно определению предела точка M0(x0, y0) (предельная точка) может и
Y |
M |
не принадлежать области определения |
функции. |
•2. В определении предела функции в
|
M0 |
|
точке M0 нет никаких ограничений на спо- |
y0 |
• |
|
соб стремления точки M к точке M0, лишь |
|
бы расстояние между этими точками стре- |
||
|
|
|
|
|
|
|
милось к нулю (а таких способов бесконеч- |
|
Uδ(M0) |
|
но много (рисунок 3)). Число A должно яв- |
|
|
ляться пределом функции при любом спо- |
|
0 |
• |
|
собе приближения M к M0. Если же резуль- |
x0 |
X |
тат зависит от способа приближения точки |
|
|
Рисунок 3 |
|
M к M0, то предел в точке M0 не существу- |
ет.
3. Бывает полезно сделать переход к полярным координатам:
x − x0 = r cosϕ , y − y0 = r sinϕ . |
|
|
|
|
|
||
Тогда lim |
f ( x, y ) = A lim f ( x0 + r cosϕ, y0 + r sinϕ ) = A независимо от ϕ. |
||||||
x→x |
r→0 |
|
|
|
|
|
|
y→ y0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Пример 3. Вычислить пределы: |
|
|
|
|
|
||
|
1) lim |
x2 y |
; |
2) lim |
|
xy |
. |
|
x2 + y2 |
x2 |
+ y2 |
||||
|
x→0 |
|
x→0 |
|
|||
|
y→0 |
|
|
y→0 |
|
|
|
● Заметим, что предельная точка O(0; 0) не входит в область определения функций, предел которых нужно вычислить.
Перейдём от декартовых координат к полярным. Для согласованных систем
имеем x = r cosϕ , y = r sinϕ. |
Ясно, что x→0 и y→0 равносильно условию r→0 |
||||||
(независимо от значения ϕ !). Следовательно, |
|
||||||
lim |
x2 y |
= lim |
r 2 cos2 ϕ r sinϕ |
= lim r cos2 ϕ sinϕ = 0 ( ϕ) , а |
|||
x2 + y2 |
|
|
|||||
x→0 |
r→0 |
r 2 |
r→0 |
||||
y→0 |
|
|
|
|
|
|
|
lim |
|
xy |
= lim |
r cosϕ r sinϕ |
= lim sinϕ cosϕ = sinϕ cosϕ , |
||
|
x2 + y2 |
|
|||||
x→0 |
r→0 |
r2 |
r→0 |
||||
y→0 |
|
|
|
|
|
|
|
т.е. зависит от ϕ, поэтому не существует. ●
Будем называть функцию z = f(M) бесконечно малой (б.м.) при M →M0, если
lim f ( M ) = 0 .
M →M0
Пользуясь определением предела функции двух переменных, можно вывести основные свойства б.м.; можно сравнивать б.м., дать понятие порядка малости и
171
эквивалентности б.м.; доказать теорему о том, что разность между функцией, имеющей предел и её пределом, есть б.м.; доказать основные теоремы об арифметических операциях над пределами. Доказательства этих теорем аналогичны соответствующим доказательствам для функций одной переменной.
Понятие непрерывности функции двух переменных вводится на основе понятия предела.
Функция z = f(M) называется непрерывной в точке M0, если предел функции в этой точке существует и равен значению функции в этой точке, т.е.
lim f ( M ) = f ( M0 ) или |
lim f ( x , y ) = f ( x0 , y0 ). |
(2) |
M →M0 |
x→0 |
|
|
y→0 |
|
Так же как и для функции одной переменной, используя определение непрерывности и соответствующие теоремы о пределах, можно доказать, что арифметические операции над непрерывными функциями двух переменных и построение сложных функций из непрерывных функций приводят к непрерывным функциям.
Точки, в которых функция не обладает свойством непрерывности, называются
точками разрыва этой функции.
Например, функция f ( x, y ) = |
|
|
x2 |
y |
|
разрывная в точке M0(0; 0), так как не |
|||
|
x2 |
+ y2 |
|||||||
|
|
|
|
|
|||||
определена в ней, но функция |
|
|
|
|
|
|
|
|
|
|
|
x2 y |
, x ≠ 0, |
y |
≠ 0 |
||||
|
|
|
|
|
|
||||
f ( x, y ) = |
|
2 + y2 |
|||||||
x |
|
|
|
||||||
|
|
|
|
|
x = 0, |
y = 0 |
|||
|
0 , |
|
|
||||||
непрерывна в точке M0(0; 0), так как f(M0)= 0 и lim |
f ( M ) = 0 (см. пример 3). |
||||||||
|
|
|
|
|
|
|
M →M0 |
|
|
Функция z = f(x, y) может иметь множество точек разрыва. Если они составляют линию, то она называется линией разрыва. Например, функция
|
1 |
|
2 |
2 |
|
z = |
|
разрывная в каждой точке окружности x |
|
+ y |
= 1. |
1 − x2 − y2 |
|
Функция u = f(M) называется непрерывной в некоторой области, если она не-
прерывна в каждой точке этой области.
В дальнейшем понадобится понятие полного приращения функции z = f(M) в точке M0, определяемое формулой ∆z = f(M) – f(M0).
Пусть точки M0 и M имеют соответственно координаты (x0, y0) и (x, y). Обозначим x – x0 = ∆x и y – y0 = ∆y, тогда получим для ∆z выражение:
∆z = f(x0 +∆x, y0 +∆y) – f(x0, y0).
Легко убедиться, что непрерывность функции z = f(M) в точке M0 равносильна
условию lim ∆z = 0 .
x→0 y→0
172
В заключение отметим, что понятия предела и непрерывности функции двух переменных легко обобщаются на функции трёх и более переменных.
2.ЧАСТНЫЕ ПРОИЗВОДНЫЕ
2.1Понятие частных производных и их вычисление
Пусть в некоторой области задана функция двух переменных z = f(x, y). Возьмём произвольную точку M(x, y) этой области и дадим аргументу x произвольное приращение ∆x, оставляя значение второго аргумента y неизменным, т.е. перейдём на плоскости от точки M(x, y) к точке M1(x+∆x, y). Тогда функция z получит приращение
∆xz = f(x +∆x, y) – f(x, y) = f(M1) – f(M),
называемое частным приращением функции z = f(x, y) по аргументу x.
Аналогично определяется и частное приращение функции z по аргументу y: |
|||||||
∆yz = f(x, y +∆y) – f(x, y) = f(M2 ) – f(M). |
|||||||
Если существует конечный предел |
|
|
|
|
|||
lim |
∆ |
x |
z |
|
lim |
∆y z |
|
|
|
|
|
, |
|||
|
|
|
|||||
∆x→0 |
∆x |
|
∆y→0 |
∆y |
|||
то он называется частной производной функции z= f(x, y) в точке M(x, y) по пе-
ременной x (по переменной y) и обозначается одним из следующих символов:
/ |
/ |
|
∂z |
|
∂f |
|
/ |
/ |
|
∂z |
|
∂f |
|
z x , |
f x |
, |
|
, |
|
z y , f y |
, |
|
, |
|
. |
||
∂x |
∂x |
∂y |
|
||||||||||
|
|
|
|
|
|
|
|
|
∂y |
||||
Из определения следует, что частная производная функции z= f(x, y) по переменной x (по переменной y) представляет собой обыкновенную производную функции одной переменной x (переменной y) при фиксированном значении другой переменной y (переменной x). Поэтому частные производные вычисляют по формулам и правилам вычисления производных функции одной переменной.
Пример 4. Найти частные производные функций: |
|
|
|||
1) z = x3 − 2 xy2 + |
y ; |
2) z = xsin y . |
|||
● 1) Считая y = const, имеем |
|
|
|
|
|
zx/ = ( x3 )x/ − 2 y2 (x)x/ + ( y )x/ = 3x2 − 2 y2 . |
|||||
При вычислении z y/ |
нужно считать x = const, поэтому |
||||
zy/ = ( x3 )/ − 2 x ( y2 )/ + ( |
y )/ = −4 xy + |
1 |
. |
||
|
|||||
y |
y |
y |
|
2 y |
|
|
|
173 |
|
|
|

2) Если y = const, то функция z является степенной функцией аргумента x, по-
этому zx/ = ( xsin y )x/ = sin y xsin y−1 .
При x = const функция z – показательная функция аргумента y, поэтому zy/ = ( xsiny )/y = xsin y ln x (sin y )y/ = xsin y ln x cos y . ●
2.2 Дифференцируемость функции
Функция z = f(x, y) называется дифференцируемой в точке M(x, y), если её полное приращение в этой точке можно представить в виде:
∆z = A(x, y)∆x + B(x, y)∆y + α1∆x + α2∆y, |
(3) |
где α1 и α2 -б.м. при∆x →0 и∆y →0 (равносильно, при r = (∆x)2 +(∆y)2 →0 ). Соотношение (3) можно записать в более короткой записи
|
α1∆x +α2∆y |
∆z = A(x, y)∆x + B(x, y)∆y + α·r, |
(4) |
гдеα = |
→ 0 при r →0 . |
|
|
|
r |
|
|
При этом слагаемое A(x, y)∆x + B(x, y)∆y, линейное относительно ∆x и ∆y, называется главной частью приращения, так как оставшееся слагаемое
α·r = α1∆x + α2∆y есть б.м. большего порядка, чем ∆x и ∆y (или, что равносильно, чем r) (советуем убедиться в этом самостоятельно).
Пример 5. Показать, что функция z = xy2 будет дифференцируемой в любой точке M(x, y).
● Запишем полное приращение:
∆z = (x + ∆x)(y +∆y)2 − xy2 = (x + ∆x)((y2 + 2y∆y + (∆y)2) − xy2 = = y2∆x + 2xy∆y + 2y∆x∆y + x(∆y)2 + ∆x(∆y)2.
Здесь y2∆x + 2xy∆y – главная часть приращения (линейная относительно ∆x и ∆y), а оставшиеся слагаемые в целом есть б.м. большего порядка малости по сравнению с ∆x и ∆y. Согласно (3), данная функция дифференцируема в любой точке
M(x, y) . ●
Выясним необходимые и достаточные условия дифференцируемости функции двух переменных.
Теорема 1 (необходимые условия дифференцируемости функции).
Если функция z = f(x, y) дифференцируема в точке M(x, y), то: 1) функция непрерывна в точке M(x, y);
2) существуют частные производные |
fx/ ( x, y ) , f y/ ( x, y ) , причём |
fx/ ( x, y ) = A( x, y ) , |
f y/ ( x, y ) = B( x, y ) . |
Доказательство. Утверждение 1) следует непосредственно из (4): lim ∆z = 0 ,
r→0
что означает непрерывность функции.
174
Для доказательства утверждения 2) положим в соотношении (3) ∆y = 0. Тогда
∆z = ∆xz = A(x, y)∆x + α·∆x, где α – б. м. при ∆x→0. Отсюда
lim |
∆x z |
= lim [A( x, y ) +α] = A( x, y ) , |
∆x→0 |
∆x |
∆x→0 |
т.е. в точке M(x,y) существует частная производная fx/ ( x, y ) = A( x, y ) . Аналогично доказывается, что в точке M(x, y) существует частная производная
f y/ ( x, y ) = B( x, y ) . Теорема доказана.
Замечание.
Обратные утверждения в теореме 1 неверны, т.е. из непрерывности функции двух переменных в точке M, а также из существования частных производных в этой точке ещё не следует дифференцируемость функции.
Теорема 2 (достаточные условия дифференцируемости функции).
Если в некоторой окрестности точки M(x,y) существуют частные производ-
ные |
fx/ ( x , y ) , |
f y/ ( x , y ) |
функции z = f(M) и эти производные непрерывны в са- |
||||
мой точке M, то функция f(M) дифференцируема в этой точке. |
|||||||
|
|
|
|
|
|
|
Доказательство. Для любых ∆x и |
Y |
|
P |
R |
N |
∆y (лишь бы точка N(x+∆x, y+∆y) не |
||
y +∆y |
● |
● |
● |
|
выходила за пределы рассматривае- |
||
|
|
|
|
|
мой окрестности) полное приращение |
||
|
|
|
|
|
|
|
|
y1 |
|
● S |
|
|
|
функции в точке M(x, y) можно запи- |
|
|
|
|
|
сать в виде: |
|||
y |
|
● |
|
|
|
∆f = f(N) − f(M) = [f(N) − f(P)] + |
|
|
|
|
|
||||
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
+ [f(P) − f(M)], |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где точка P имеет координаты |
0 |
|
x |
x1 |
x+∆x X |
(x, y+∆y) (рисунок 4). Выражение в |
||
|
первой квадратной скобке можно рас- |
||||||
|
|
|
Рисунок 4 |
|
|
сматривать как приращение функции |
|
f(x,y+∆y) одной переменной x (так как второй аргумент функции сохраняет постоянное значение y+∆y).
Аналогично, выражение во второй квадратной скобке есть приращение функции f(x,y) одной переменной y (так как первый аргумент сохраняет постоянное значение x).
Применяя формулу Лагранжа, имеем
f(N) − f(P) = f(x +∆x, y +∆y) − f(x, y +∆y) = |
fx/ ( x1 , y + ∆y )∆x = fx/ ( R )∆x , |
||
f(P) − f(M) = f(x, y +∆y) − f(x, y) = |
f / ( x, y |
1 |
)∆y = f / ( S )∆y , |
|
y |
y |
|
где x1 и y1 – предусмотренные формулой Лагранжа промежуточные значения x и y между x и x +∆x, y и y +∆y соответственно.
Используя условие теоремы о непрерывности частных производных, представим
175
fx/ ( R ) и f y/ ( S ) в виде: fx/ ( R )= fx/ ( M ) +α1, f y/ ( S ) = f y/ ( M ) +α2, где
α1 и α2 – б. м. при ∆x→0 и ∆y→0, т.е. при N→M и, следовательно, при R→M и S→M. Тогда имеем:
∆f = fx/ ( R )∆x + f y/ ( S ) ∆y = [ fx/ ( M ) +α1]∆x +[ f y/ ( M ) +α2]∆y = = fx/ ( M ) ∆x + f y/ ( M ) ∆y +α1∆x + α2∆y.
Итак, полное приращение ∆f представимо в виде (3), что означает дифференцируемость функции в точке M.
2.3 Частные производные высших порядков
Пусть у функции z = f(x, y) существуют частные производные fx/ ( x, y ) и f y/ ( x, y ) в некоторой окрестности точки M(x, y). В этом случае частные произ-
водные представляют собой функции двух переменных x и y, определённые в ок-
рестности точки M. Назовём их частными производными первого порядка.
Частные производные по x и y от функций fx/ ( x, y ) и f y/ ( x, y ) , если они
существуют, называются частными производными второго порядка от функции z = f(x, y) и обозначаются следующим образом:
f |
// |
= z |
// |
= |
∂2 f |
= |
∂2 z |
, |
|
|||
xx |
xx |
∂x2 |
∂x2 |
|
||||||||
|
|
|
|
|
|
|
||||||
|
// |
|
// |
|
|
∂2 f |
|
|
|
∂2 z |
|
|
f yx = zyx = |
|
|
|
= |
|
|
, |
|||||
|
∂y∂x |
∂y∂x |
||||||||||
|
|
|
|
|
|
|
|
|
||||
Итак, по определению: fxx// = ( fx/ )x/ ,
// |
|
|
// |
|
|
∂2 f |
|
|
∂2 z |
|
|||||
fxy |
= zxy = |
|
|
|
|
|
= |
|
|
|
, |
||||
|
∂x∂y |
∂x∂y |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
f |
// |
= z |
// |
= |
∂2 f |
= |
∂2 z |
. |
||||||
|
yy |
yy |
∂y2 |
∂y |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
∂ |
2 z |
|
= |
∂ |
∂z |
и т.д. |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
∂x∂y |
|
|
|
|||||||||||
|
|
∂y |
∂x |
|
|
|
|
|
|||||||
В свою очередь, частные производные второго порядка снова являются функциями двух переменных.
Частные производные третьего, четвёртого, ..., n -го порядков и соответствующая символика вводятся аналогично.
Частная производная любого порядка, взятая по различным переменным, (на-
пример, |
∂2 z |
, |
∂2 z |
, |
∂3 z |
, |
∂3 z |
, ...) называется смешанной. |
|
∂x∂y |
∂y∂x |
∂x∂y∂x |
∂y∂x∂x |
||||||
|
|
|
|
|
Ясно, что для функции двух переменных можно, вообще говоря, определить две частные производные 1-го порядка, четыре частных производных 2-го порядка, восемь – 3-го порядка и, вообще, 2n производных n -го порядка.
Пример 6. Вычислить все частные производные функции z = x4 +5x2y2 до 3-го порядка включительно.
● Имеем
z/x= 4x3+10xy2, z/y= 10x2y, z//xx= 12x2+10y2, z//xy= 20xy, z//yx= 20xy,
176
