
Matematika_Zaytsev_ch2
.pdf
Отметим, что импликация не полностью соответствует обычному пониманию слов «если ... , то ...» и «следует». Из определения импликации следует, что если А
ложно, то, каково бы ни было В, высказывание А В считается истинным, т.е. из неверного утверждения следует все что угодно. Например, высказывание «если
крокодил – насекомое, то среднегодовая температура в Арктике равна +30С°»
является истинным.
Для сокращения и уточнения записи высказываний вводят два знака и ,
называемых соответственно кванторами общности и существования.
Запись x X A( x ) означает: «для любого элемента x X истинно утверждение А(x)».
Запись x X : A( x ) означает: «существует элемент x X такой, что для него истинно утверждение А(x)».
Если элемент x X, для которого истинно утверждение А(x), не только существует, но и единственный, то пишут ! x X : A(x).
Введенными символами удобно пользоваться, например, при определении операций над множествами. Так,
A U B : {x : ( x A ) ( x B )} , A I B : {x : ( x A ) ( x B )} ,
A \ B : { x : ( x A ) ( x B ) } , A : { x : ( x E ) ( x A ) } ,
где символ : означает эквивалентность по определению.
2.2 Взаимно обратные и взаимно противоположные теоремы. Необходимые и достаточные условия
Рассмотренные логические символы и кванторы существования и общности широко используются в математике для записи высказываний. Эти высказывания представляют собой устанавливающие свойства математических объектов теоремы, утверждения и следствия из них, а также различные формулы. Однако следует отметить, что часть высказываний приходится все же выражать словами.
Теорема состоит в задании некоторого свойства А, называемого условием, из которого выводят свойство В, называемое заключением. Коротко теорему «А вле-
чёт В» можно записать в виде А В. Рассмотрим, например, следующие теоремы.
Теорема 1. Если сумма цифр натурального числа делится на 3, то и число делится на 3.
Теорема 2. Если хотя бы одно из двух чисел делится на 7, то и их сумма делится на 7.
Теорема 3. Если параллелограмм – ромб, то его диагонали взаимно перпендикулярны.
21
Теорема 4. Если четырёхугольник является прямоугольником, то его диагонали равны.
В теореме 1 речь идет о двух высказываниях:
А: сумма цифр числа n делится на 3, В: число n делится на 3.
Из арифметики известно, что высказывание А В истинно n N , т.е. теорема
1верна.
Втеореме 2 говорится о двух высказываниях:
А: n или m делится на 7, B: n + m делится на 7.
Высказывание А В n,m N очевидно ложно и, следовательно, теорема 2 неверна.
В теореме 3: А: параллелограмм – ромб, B: диагонали параллелограмма взаимно перпендикулярны.
В теореме 4: А: четырехугольник – прямоугольник, B: диагонали четырёхугольника равны.
Из курса геометрии известно, что высказывание А В истинно (как в случае теоремы 3, так и в случае теоремы 4), поэтому теоремы 3 и 4 верны.
Чёткое и однозначное выделение в каждой теореме условия и заключения позволяет однозначно определить понятия обратной и противоположной теорем.
Теоремы А В и В А называются взаимно обратными. Иногда одну из этих теорем называют прямой, тогда другую называют обратной. Важно понимать, что для пары взаимно обратных теорем могут осуществляться все три возможности:
1)Обе теоремы верны, в этом случае теорему можно записать в виде А В. Эта запись соответствует фразе «А тогда и только тогда, когда В». Так, например, верна теорема 1 и обратная ей теорема (если число делится на 3, то сумма цифр числа делится на 3).
2)Одна из теорем верна, другая неверна. Так, теорема 4 верна, а обратная ей теорема (если диагонали четырехугольника равны, то четырехугольник является прямоугольником) неверна.
3)Обе теоремы неверны, как, например, теорема 2 и ей обратная.
Если верна теорема А В, то говорят, что А является достаточным условием для В, а В – необходимым условием для А. Так, в теореме 1 условие А является достаточным условием для В, т.е. для того, чтобы натуральное число делилось на 3, достаточно, чтобы сумма цифр этого числа делилась на 3. Условие В является необходимым условием для А, т.е. для того, чтобы сумма цифр натурального числа делилась на 3, необходимо, чтобы само это число делилось на 3.
Если верна теорема А В, т.е. верна прямая теорема и обратная ей, то А явля-
ется необходимым и достаточным условием для В, а В – необходимым и доста-
точным условием для А. Например, теорема 1 и ей обратная, могут формулиро-
ваться так: «Чтобы натуральное число делилось на 3, необходимо и достаточно, чтобы сумма цифр этого числа делилась на 3».
22
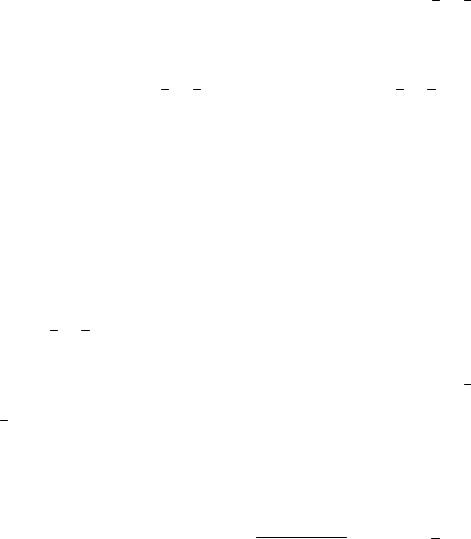
Перейдём к понятию противоположной теоремы: теоремы А В и A B называются взаимно противоположными. Следовательно, если в формулировке некоторой теоремы заменить условие и заключение их отрицаниями, то получится формулировка теоремы, противоположной исходной.
Всякая теорема А В порождает, таким образом, ещё три теоремы: обратную
В А, противоположную A B и противоположную обратной B A .
Например, взяв в качестве исходной верную теорему 4, будем иметь:
1)обратная теорема: если диагонали четырехугольника равны, то четырехугольник является прямоугольником (теорема неверна);
2)противоположная теорема: если четырехугольник не является прямоугольником, то его диагонали не равны (теорема неверна);
3)противоположная обратной: если диагонали четырехугольника не равны, то четырехугольник не является прямоугольником (теорема верна).
В рассмотренном примере прямая теорема и противоположная обратной оказались истинными, а обратная и противоположная – ложными. Это совпадение не является случайным. Прямая теорема и теорема противоположная обратной либо обе истинны, либо обе ложны. Часто доказательство одной из этих теорем вызывает трудности, в таком случае следует попытаться доказать другую.
Известный метод доказательства от противного как раз и состоит в том, что
вместо исходной теоремы А В доказывают противоположную обратной. Если теорема B A окажется верной, то А ложно, т.е. возникает противоречие с тем, что А истинно.
Если в символьную запись высказывания А входят кванторы , и условие Р, то при построении символьной записи противоположного высказывания А квантор заменяют на , квантор – на , а условие Р заменяют на условие
P .
Пример 10. Записать отрицания высказываний: x E P( x ) (для каждого элемента х множества Е имеет место свойство Р(x)) и x E : P( x ) (су-
ществует элемент x множества Е, обладающий свойством Р(x)).
• Если первое высказывание неверно, то свойство Р(x) имеет место не для каждого элемента указанного множества, т.е. существует хотя бы один элемент
x E , не обладающий этим свойством, т.е. x E P( x ) x E : P( x ) . Теперь построим отрицание высказывания x E : P (x). Если это высказы-
вание ложно, то указанного элемента не существует, т.е. для каждого |
x E свой- |
|||||
ство Р(x) не выполняется, т.е. |
|
x E |
|
|
|
|
x E : P( x ) |
• |
|||||
P( x ) . |
||||||
Замечание. Очень важно понимать, что для того, чтобы опровергнуть высказывание x E P( x ) , достаточно указать только один элемент x E , при
котором условие Р(x) будет не выполняться. Такой элемент x E называется контрпримером для высказывания x E P( x ) .
23
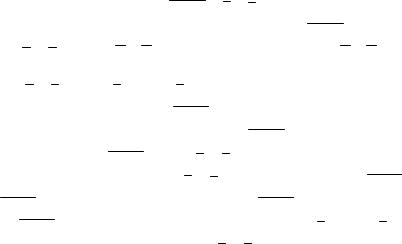
Например, для высказывания n N (число n2 + n + 41 – простое) элемент n = 40 является контрпримером. Действительно, число 402 + 40 + 41 = 40 41+ 41 делится на 41, т.е. не является простым числом, значит условие (число n2 + n + 41
– простое) не выполняется при n = 40. Замечательно, что для всех n < 40 рассматриваемое высказывание истинно.
Доказательство утверждений представляет собой проводимое по определённым правилам рассуждение, в котором для обоснования сформулированного утверждения используют определения, аксиомы и ранее доказанные утверждения.
Пример 11. Показать, что для абсолютного значения (модуля) |x| любого x R справедлива теорема:
|x| < ε – ε < x < ε, где ε – некоторое положительное число.
•Напомним, что по определению
x, если x ≥ 0,
| x |= − <x, если x 0.
Вначале докажем прямую теорему: |x| < ε – ε < x < ε.
В самом деле, если x ≥ 0, то – ε < x и |x| = x < ε, т.е. – ε < x < ε. Если же x < 0, то x < ε и |x| = – x < ε. Второе из этих неравенств равносильно неравенству
x > – ε. Поэтому и в этом случае – ε < x < ε.
Докажем обратную теорему: – ε < x < ε |x| < ε.
Двойное неравенство – ε < x < ε равносильно неравенствам x < ε и – x < ε. Тогда, если x ≥ 0, то |x| = x < ε, а если x < 0, то |x| = – x < ε, т.е. в любом случае справедливо |x| < ε. •
Пример 12. Доказать справедливость формулы для множеств А и В:
АU B = АI B .
•Если это равенство верное, то каждый элемент x A U B должен принадле-
жать и АI B , т.е. x АI B . Предположим противное: x АI B . Тогда справедливы импликации:
x A I B ( x A ) ( x B ) ( x A ) ( x B )x A U B x A U B .
А это противоречит исходному условию x A U B , что доказывает справедливость импликации x A U B x АI B .
Наоборот, каждый элемент x АI B должен принадлежать и A U B , т.е. x A U B . Снова предположим противное: x A U B , тогда
x A U B x A U B ( x A ) ( x B ) ( x A ) ( x B )x A I B .
24

Это опять противоречит исходному условию x АI B , что доказывает справедливость обратной импликации высказываний: x АU B x АI B .
Витоге справедливость формулы доказана полностью. •
3.ЗАДАЧИ
3.1 Задачи с решениями
1. Записать указанные множества, используя различные формы записи: А – множество всех чётных натуральных чисел;
B – множество целых чисел от –3 до 193; С – множество нулей функции f(x) = x3 – 4x; D – множество корней уравнения sinx = 0,5;
E – множество рациональных чисел, квадрат которых равен 2;
F – множество комплексных чисел, модуль которых равен 1;
G – множество точек плоскости, лежащих на биссектрисе 1-го и 3-го координатных углов.
• Так как чётное натуральное число должно без остатка делиться на 2, то
A = {2, 4, 6, 8, ... } = {x: x = 2n , n N}.
Множество B можно задать перечислением таких целых чисел:
B = {–3, –2, –1, 0, 1, 2, 3, ..., 192, 193}
или указав свойство: B = {x Z: –3 ≤ x ≤ 193}.
Нулями функции f(x) являются корни уравнения f(x) = 0, поэтому
C = {x : x3 – 4x = 0} = {x: x(x–2)(x+2) = 0} = {0; 2; –2}.
|
n |
|
π |
|
Множество D = {x: sinx = 0,5} = x : x = ( −1 ) |
6 |
+ nπ, n Z . |
||
|
|
|
|
|
Было показано, что не существует рационального числа, квадрат которого был бы равен 2, поэтому E = {x Q : x2 = 2}= .
Запишем множество F, используя различные формы записи комплексного чис-
ла:
F = {z C: |z| = 1} = {z: z = cosϕ + isinϕ , ϕ [0, 2π)}= {z: z = eiϕ}.
Определяющим свойством элементов множества G является равенство абсциссы и ординаты точек плоскости R2, поэтому G = {(x, y) R2 : x = y }. •
2. Данные множества описать перечислением всех своих элементов:
|
|
1 |
≤ 2x < 5 |
|
|
а) A = {x R : x3 – 3x 2+ 2x = 0}; б) B = x Z : |
|
; |
|||
4 |
|||||
в) C ={x R : cos2 2 x = 1 , 0 < x ≤ 2π} . |
|
|
|
||
• а) Элементы x множества A являются действительными корнями уравнения x3 – 3x2 + 2x = 0. Решим его: x(x2 – 3x + 2) = 0 x1 = 0, x2 = 1, x3 = 2.
25
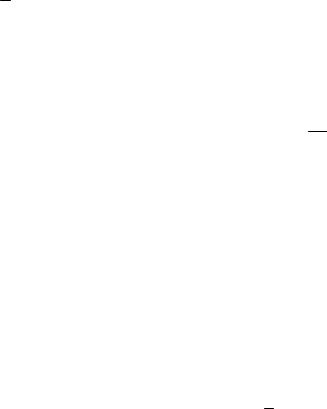
Итак, А = {0; 1; 2}.
б) Для нахождения элементов множества B решим неравенство:
41 ≤ 2x < 5 2−2 ≤ 2x < 2log2 5 −2 ≤ x < log2 5 . Так как log2 4 < log2 5 < log2 8 , то 2 < log2 5 < 3. Поэтому
В = {x Z : –2 ≤ x < 3} = {–2; –1; 0; 1; 2}.
в) Элементы множества C определяются из решения уравнения cos22x = 1 или cos2x = ±1 при x (0, 2π].
В случае cos2x = 1 получим 2x = 2nπ, n = 1, 2, поэтому x = π, x = 2π, а в случае cos2x = –1 получим 2x = (2n + 1) π, n = 0, 1, поэтому x = π2 , x = 32π .
Итак, C = |
π |
; π ; |
3π |
; 2π |
. • |
|
2 |
2 |
|||||
|
|
|
|
3. Задать с помощью определяющего свойства следующие множества:
а) А = {1; 2; 4; 8; 16; ...}; |
|
|
|
|
4 |
|
6 |
|
8 |
|
|||||||||||
б) |
B = |
|
2; |
|
; |
|
; |
|
|
; K ; |
|||||||||||
3 |
5 |
7 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 |
|
3 |
|
4 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
в) C = |
− |
|
; |
|
; − |
|
; |
|
; K . |
|
|
|
|
|
|
|
|
|
|
||
3 |
4 |
5 |
6 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
• а) Заметим, |
что выписанные элементы являются членами геометрической |
||||||||||||||||||||
прогрессии bn, первый член которой равен 1, а знаменатель q = 2. Общий (n - член этой прогрессии равен bn = 1 qn−1 = 2n−1 . Поэтому A ={2n−1 ,n N} .
Можно было сразу заметить, что на n - м месте находится элемент равный 2n−1
б) Если представить первый элемент множества В в виде 21 , то можно заме-
й )
.
тить, что каждый элемент этого множества представляет собой дробь, в числителе которой находятся чётные числа, а в знаменателе нечётные числа. Поэтому,
|
2n |
|
|
B = |
|
,n N . |
|
2n − 1 |
|||
|
|
Легко проверить истинность этой записи, подставляя в эту дробь числа n = 1, 2, 3, ... .
в) Чередование знака можно задать выражением ( −1 )n ,n N . Действительно,
при n = 1 имеем (–1)n = –1, при n = 2 будет (–1)n = +1, при n = 3 будет (–1)n = – 1 и т.д. Легко заметить, что на любом n-м месте в записи элемента множества С числитель дроби на единицу больше n, а знаменатель больше n на два. Поэтому
|
n |
|
n + 1 |
|
|
|
C = ( −1 ) |
|
|
,n N . |
• |
||
n + 2 |
||||||
|
|
|
|
|
||
26
4. В группе из 100 туристов 70 человек знают английский язык, 45 знают французский и 23 человека знают оба языка. Сколько туристов в группе не знают ни английского, ни французского языка?
• Множество туристов данной группы, знающих английский язык, обозначим А, знающих французский – В. Тогда туристы, знающие и тот и другой язык, обра-
зуют множество A I B . По условию n(A) = 70, n(B) = 45, n( A I B ) = 23.
По формуле (7) находим n( A U B ) =70 + 45 − 23 = 92 .
Множество A U B есть множество туристов, знающих хотя бы один из этих двух
языков, следовательно, не знают ни французский, ни английский 100 – 92 = 8 туристов группы. •
5. Пусть А – множество делителей числа 15, В – множество простых чисел, меньших 10, С – множество натуральных чётных чисел, меньших 9. Перечислить элементы этих множеств и найти
A U B, A UC , B IC , ( A UC ) I B, A I B IC .
• Имеем A = {1; 3; 5; 15}, B = {2; 3; 5; 7}, C = {2; 4; 6; 8}.
Напомним, что простым числом является натуральное число, делителями которого являются только числа 1 и само число. Число 1 не является простым числом.
Пользуясь определением объединения и пересечения множеств, получим
A U B ={1; 2; 3; 5;7 ; 15}, B IC ={2}, A UC ={1; 2; 3; 4; 5; 6; 8; 15}.
Поэтому, ( A UC ) I B ={2; 3; 5}. Множества A и C не имеют общих элементов, значит A IC = , A I B IC = . •
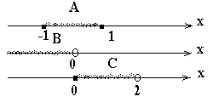
6. Пусть A = [–1; 1], B = (–∞; 0), C = [0; 2). Найти следующие множества:
A UC , A I B, A U B UC , ( A U B ) IC , B IC .
• Для наглядности изобразим множества A, B, C на числовой прямой (рисунок 4).
Рисунок 4 Исходя из определения объединения и пересечения множеств, получаем:
A UC = [ −1;2 ), A I B = [ −1; 0 ), A U B UC = ( −∞; 2 ), ( A U B ) IC = [0;1], B IC = . •
7. Найти A I B, A U B , если
A = {x Z : x делится на 3}; В = {x Z : x не делится на 6}.
• Рассмотрим числа, которые одновременно делятся на 3 и не делятся на 6. Это следующие числа: {±3; ±9; ±15; ... }. Поэтому A I B = {3k : k – нечётные целые
27

числа} = {3 (2k + 1): k Z}, A U B = Z, так как, если x делится на 3, то x A, а если не делится на 3, то, очевидно, x не делится и на 6, т.е. x В. Итак, обязательно выполняется хотя бы одно из условий x A, x В. •
8. Решить уравнение z2 + 3z + 3 = 0.
• Найдём дискриминант квадратного уравнения: D = (–3)2 – 4 1 3 = –3. Так как D < 0, то корнями этого уравнения будут комплексные числа. Учитывая,
что |
|
D = −3 = |
( −1 ) 3 = i |
|
3 , получим корни: |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
z1 = −3 + i 3 = − |
3 |
|
+ i |
|
3 |
, z2 = |
−3 − i 3 = − |
3 |
− i |
3 |
. • |
|||||||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
||||||
|
z1 |
9. Для комплексных чисел z1 = 1 + i и |
z2 = 1 – 3i найти 2z1 – 3z2, z1 z2, |
|||||||||||||||||||||||||
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
z2 |
|
2z1 – 3z2 = 2(1+i) – 3(1 – 3i) = 2 + 2i – 3 + 9i = –1 + 11i, |
|
|
|||||||||||||||||||||||
|
|
|
• |
|
|
|||||||||||||||||||||||
|
|
|
|
|
z1 z2 = (1 + i) (1 – 3i) = 1 – 3i + i – 3i2 = 1 – 2i + 3 = 4 – 2i, |
|||||||||||||||||||||||
|
|
z |
1 |
= |
1 + i |
= |
( 1 + i )( 1 + 3i ) |
|
|
= |
|
1 + 3i + i + 3i |
2 |
= |
1 + 4i − 3 |
|
= −0,2 + 0,4i . • |
|||||||||||
|
|
z2 |
1 − 3i |
( 1 |
− 3i )( 1 + |
3i ) |
|
|
1 − ( 3i )2 |
|
1 + 9 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
10. Найти все значения 6 −64 .
• Запишем число w = – 64 в тригонометрической форме:
– 64 = 64(cosπ + i sinπ).
Применяя формулу (6), получим различные значения:
|
|
|
|
|
|
π + 2πk |
+ i sin |
π + 2πk |
|
|
|
|
|
|
|||||||
|
|
zk = 6 64 cos |
|
|
6 |
6 |
,k = 0, 1, 2, 3, 4, 5. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z |
= 2(cos π + i sin π ) = 3 + i , |
z |
1 |
= 2(cos π + i sin π ) = 2i , |
|
||||||||||||||||
0 |
|
|
6 |
|
6 |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
z2 = 2(cos |
5π |
+ i sin |
5π |
) = − 3 + i , |
z3 = 2(cos |
7π |
+ i sin |
7π |
|
) = − 3 − i , |
|||||||||||
6 |
|
6 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
6 |
6 |
|
|
|||||||
z4 = 2(cos |
3π |
+ i sin |
3π |
) = −2i , |
z5 |
= 2(cos |
11π |
+ i sin |
11π |
) = 3 − i . • |
|||||||||||
2 |
|
2 |
|
|
|
||||||||||||||||
11. |
|
|
|
|
|
|
|
|
|
|
6 |
|
|
6 |
|
|
|
||||
Определить значения истинности следующих высказываний: |
|
||||||||||||||||||||
|
А1 |
: берёза – дерево ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
А2 |
: y = x2 – чётная функция; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
A3 |
: π2 = 1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
A4 |
: α R sin2α + cos2α = 1; |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
A5 : x R 2x – 5 = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
A6 |
: x N : sinx = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
28

А7 : число 221 – простое;
A8 : около любого прямоугольника можно описать окружность; А9 : в любой прямоугольник можно вписать окружность;
А10 : разность длин двух сторон любого треугольника всегда меньше длины третьей стороны.
• Очевидно, что |A1| = И.
Так как y = (–x)2 = x2, то функция y = x2 действительно чётная, поэтому |A2| = И.
|A3| = Л, так как π ≈ 3,14.
|A4| = И, так как sin2α + cos2α = 1 – основное тригонометрическое тождество. Уравнение 2x – 5 = 0 истинно только при x = 2,5, поэтому |A5| = Л.
Корни уравнения sinx = 0 можно записать в виде x = nπ, n Z. Очевидно, что среди этих чисел нет натуральных, поэтому |A6| = Л.
Так как число 221 = 13 17, то оно не является простым, значит |A7| = Л. Вспомним, что окружность можно описать около четырехугольника, если сум-
ма противоположных углов равна 180°. В любом прямоугольнике это условие выполняется, значит |A8| = И.
В четырехугольник можно вписать окружность, если сумма длин противоположных сторон одинакова. Так как в некоторых прямоугольниках это не выполняется, то |A9| = Л.
|A10| = И, это следует из очевидного факта – сумма длин двух сторон треугольника всегда больше длины третьей стороны. •
12. Заданы высказывания:
A : 2 2 > 4 ; B : y = tgx – периодическая функция;
С : клубника – ягода; |
D : уравнение 1 – х = 0 не имеет корней. |
||
Определить значения истинности следующих высказываний: |
|||
а) С (A D); |
б) B C A ; |
||
в) ( B |
A |
) C ; |
г) (A C) (D B). |
• Вначале определим значения истинности заданных высказываний:
|A| = Л, |B| = И, |C| = И, |D| = Л.
Чтобы определить значения истинности для высказываний, полученных из данных в результате логических операций, воспользуемся таблицами истинности (см.
с. 20)
а) |A D| = Л как дизъюнкция двух ложных высказываний.
|C (A D)| = Л как импликация, у которой посылка истинна, а заключение ложно.
б) |B C| = И как конъюнкция двух истинных высказываний.
|B C A| = Л как эквиваленция двух высказываний, одно из которых ложно, а другое истинно.
в) A = И , поэтому B A = И , | ( B A ) C | = И .
г) |A C| = И, |D B| = Л, поэтому |(A C) (D B)| = Л. •
29

13. Записать высказывания, вводя буквенные обозначения для входящих в них более простых высказываний. Определить значения истинности этих высказываний:
а) так как число 40 делится на 10, то это число делится или на 3, или на 5; б) неверно, что 21 делится на 2 и на 11; в) число 21 не делится ни на 2, ни на 11;
г) равенство сторон треугольника необходимо для равенства всех внутренних углов треугольника;
д) равенство всех сторон четырехугольника достаточно для того, чтобы он являлся квадратом.
• а) Обозначим высказывание А: число 40 делится на 10, |A| = И; В: число 40
делится на 3, | В | = Л; С: число 40 делится на 5, |С| = И. Тогда высказывание
А (B C) будет истинным, так как |B C| = И.
|
|
б) Пусть А: число 21 делится на 2, |A| = Л; |
B: число 21 делится на 11, |
||||||||||||||||||
|В| = Л. Тогда A B : число 21 делится на 2 и на 11, |
|
A B |
|
|
= Л. Искомое вы- |
||||||||||||||||
|
|
||||||||||||||||||||
сказывание |
|
|
и | |
|
|= И . |
|
|
|
|
|
|
|
|
|
|
|
|||||
A B |
A B |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
в) Используя обозначения пункта б), имеем: |
|
|
: число 21 не делится на 2, |
||||||||||||||||
|
|
|
A |
||||||||||||||||||
| |
A |
| = И ; |
B |
: число 21 не делится на 11, | |
B |
| = И ; |
|
|
A |
|
B |
– искомое выска- |
|||||||||
зывание и | A B | = И.
г) Пусть А: стороны треугольника равны; В: внутренние углы треугольника равны. Так как В А истинно (известно из школьного курса геометрии), то А является необходимым условием для В. Высказывание в пункте г) истинно.
д) Пусть А: стороны четырехугольника равны; В: четырехугольник является квадратом. Так как теорема А В неверна, то высказывание пункта д) ложно. •
3.2 Задачи для самостоятельного решения
1. Записать указанные множества, используя различные формы записи: A1 : множество всех натуральных нечётных чисел;
A2 : множество всех чисел, которые делятся на 7;
A3 : множество целых чисел, являющихся корнями уравнения 6x2 – x – 1 = 0 ; A4 : множество делителей числа 160;
A5 : множество иррациональных корней уравнения x3 – 3x = 0;
A6 : множество комплексных чисел, имеющих аргументом число π |
2 |
. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2. Описать перечислением всех своих элементов следующие множества: |
|
|
|
|||||||
|
2 |
|
|
1 |
|
|
|
|
|
|
а) A = {x N : x |
|
– 3x – 4 ≤ 0}; |
б) В = x R : x + |
|
≤ 2 |
x > |
0 |
|
; |
|
|
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
в) C = {x Q : 2x3 – x2 + 4x = 2}; |
г) D = {x C : x2 + x + 1 = 0}. |
|
|
|
||||||
3. Задать с помощью определяющего свойства следующие множества:
30
