2. Статика текучего тела (гидростатика)

2.1. Гидростатическое давление

Гидростатика – раздел гидромеханики, в котором изучают жид­кости, находящиеся в условиях равновесия (покоя). Из определения текучести физических тел следует, что в состоянии покоя в жидкости и газе касательные напряжения равны нулю, и в каж­дой точке, произвольно ориентированной в пространстве площадки, дей­ствуют только нормальные напряжения. Возьмем произвольную площад­ку (рис. 2.1, а), имеющую единичный вектор нормали n = (n_x, n_y, n_z). Поскольку вектор напряжений на этой площадке р_n параллелен n, то можно записать

, (2.1.1)

где р_nn – проекция р_n на нормаль к площадке; очевидно, р_nn = р_n . С другой стороны, согласно (1.4.10) имеем

. (2.1.2)

Сравнивая выражения (2.1.1) и (2.1.2), найдем

, (2.1.3)

Рис. 2.1. Гидростатическое давление:

а  в точке сплошной среды;

б  на поверхности произвольной формы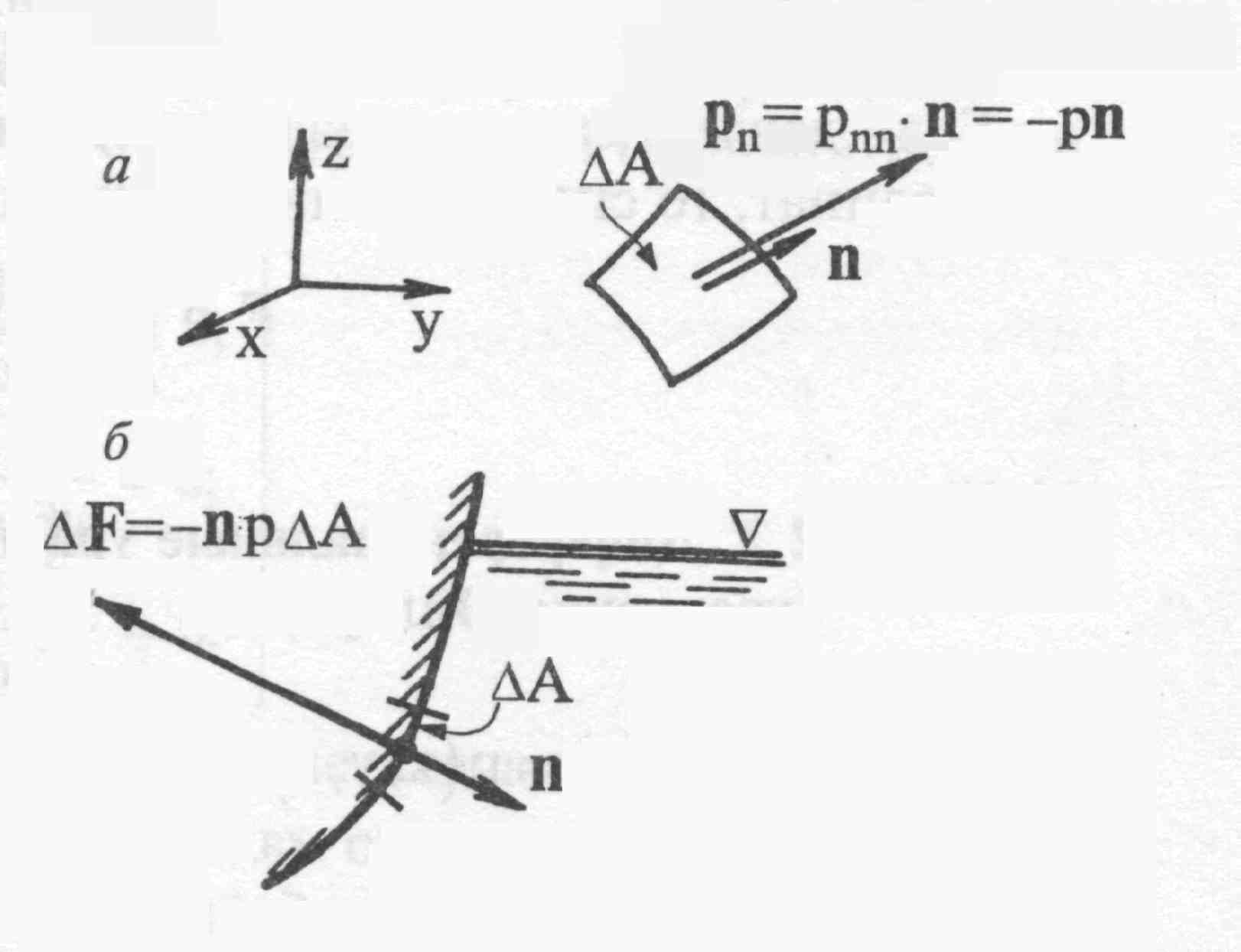

откуда следует, что значение нормального напряжения в фиксированной точке покоящейся жидкости не зависит от ориентации площадки.

При рассмотрении напряжен­ного состояния сплошной среды принято растягивающие напряже­ния считать положительными. В то же время в большинстве задач технической механики жидкости во избежание разрывов сплошно­сти рас­тягивающие напряжения в жидкой среде считаются недопустимыми. Это в еще большей степени от­носится к газообразной среде. По­этому в гидростатике в качестве основной величины, характеризу­ющей напряженное состояние жидкости, вводят взятое со зна­ком плюс нормальное напряжение (которое на всех произвольно ориентированных площадках в данной точке имеет одинаковое значение). Эта величина, являющаяся частным случаем гидродинамического давления (1.4.12), называется гидростатическим давлением и обозначается через р:

. (2.1.4)

Отсюда ясно, почему в зависимости (1.4.12) стоит знак минус, определяющий величину гидродинамического давления.

Матрица тензора напряжений в условиях покоя текучего тела имеет вид

. (2.1.5)

Если тензорную единицу обозначить через Е, то тензор напряжения в покоящейся жидкости можно представить в виде

П = – рЕ. (2.1.6)

Таким образом, напряжённое состояние в покоящейся жидкости определяется величиной р, поэтому его характеризуют не тензором П, а считают, что оно полностью описывается величиной гидростатического давления, которое можно рассматривать как скаляр.

Сила гидростатического давления F (рис.2.1,б), действующая на малую площадку А, – это вектор, направленный со стороны жидкости по нормали к этой площадке (такая нормаль обычно называется внутренней и её вектор равен (-n)):

. (2.1.7)

Если давление на площадке конечных размеров А (рис.2.1,б) зависит от координат, то сила давления на эту площадку определяется по формуле:

. (2.1.8)

2.2. Дифференциальные уравнения равновесия текучего тела (уравнения эйлера)

Пусть  давление в жидкости. Выделим внутри жидкости куб с бесконечно малыми рёбрами dx, dy, dz и рассмотрим его равновесие под действием объёмных и поверхностных сил (рис.2.2).

Приравняем к нулю сумму проекций на ось х всех сил, действующих на куб.

Рис. 2.2. К выводу дифференциальных уравнений равновесия текучего тела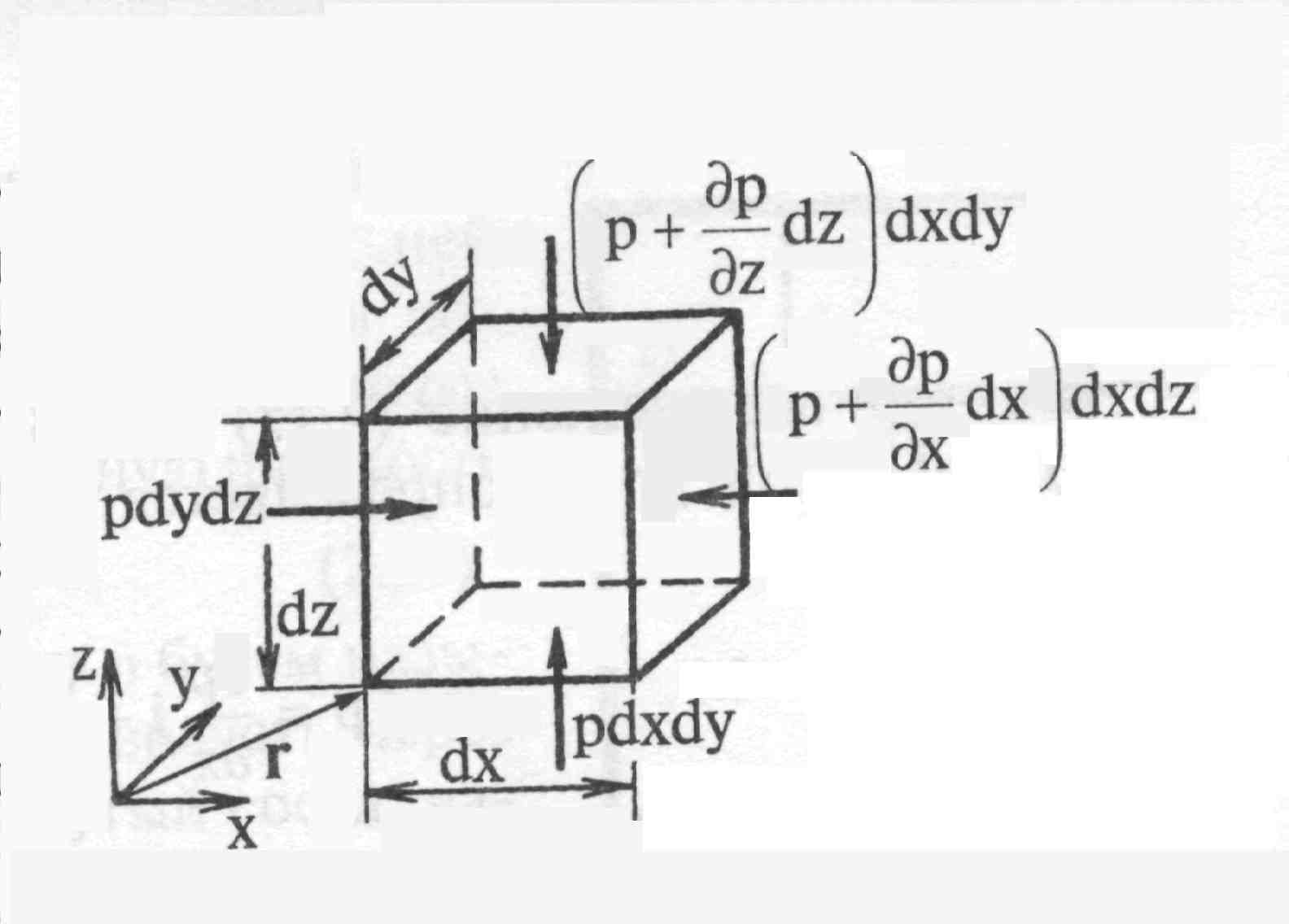

Плотность распределения массовой (объёмной) силы обозначим , тогда объёмная сила, действующая на куб, будет иметь проекцию на ось х, равную .

Поверхностные силы на грани, нормальные осям y и z, дают нулевую проекцию на ось х, так как касательные напряжения в условиях гидростатики равны нулю. В пределах куба считаем, что в разложении р(х,у,z) в ряд Тейлора можно принять в расчёт лишь члены, линейно зависящие от приращения координат. Обозначим давление на левую грань куба, перпендикулярную оси х, через р(х,у,z), при этом на правой грани давление будет равно . Если считать эти грани элементарными площадками в отношении давления, то проек­ция на ось х силы давления на левую грань равна рdydz, а на правую равна . Сумма проекций всех поверхностных сил на ось х при этом окажется равной

.

Приравняв нулю сумму проекций поверхностных и объемных сил на ось х, имеем:

. (2.2.1)

Разделив все слагаемые на рdxdydz, получим первое уравнение рав­новесия. Два других уравнения выведем аналогичным образом, проекти­руя силы на оси у и z. В результате получим систему дифференциальных уравнений равновесия (покоя) текучего тела (уравнений гидростатики Эй­лера):

(2.2.2)

Введём единичные векторы i, j и k, соответствующие координатным осям х, у и z:

. (2.2.3)

Умножим (2.2.2) на i, j и k, соответственно, и сложим их:

или в векторной форме

. (2.2.4)

Векторное уравнение (2.2.4) равносильно системе трёх уравнений (2.2.3), где вектор grad p определяется через свои проекции на координатные оси в виде

(2.2.5)

либо в матричной форме

. (2.2.6)