
- •1. Введение в механику сплошной среды
- •1.1. Предмет и метод механики сплошной среды
- •1.2. Плотность распределения гидромеханических характеристик в сплошной среде
- •1.3. Физические свойства жидкостей и газов
- •2. Статика текучего тела (гидростатика)
- •2.1. Гидростатическое давление
- •2.2. Дифференциальные уравнения равновесия текучего тела (уравнения эйлера)
- •2.3. Интегрирование уравнений эйлера
- •2.4. Способы измерения гидростатического давления
- •3. Кинематика сплошной среды
- •3.1. Движение точки с позиций теоретической механики
- •3.2. Методы описания движения сплошной среды
- •3.3. Поток гидромеханической характеристики через поверхность
- •3.4. Гидромеханическая интерпретация теоремы остроградского гаусса
- •3.5. Циркуляция скорости. Вихрь вектора скорости
- •3.6. Поля в гидродинамике
- •3.6.1.Операции над тензорами
- •4. Напряжения и деформации в твёрдых средах
- •4.1. Силы, действующие на текучее тело
- •4.2. Напряжённое состояние в точке сплошной среды. Тензор напряжений
- •4.3. Элементарные деформации. Коэффициент пуассона
- •Напряжений, действующих на грани кубика
- •5.2. Напряжения и деформации в твёрдых средах с точки зрения геодинамики
- •5.3. Упругие деформации
- •5.3.1.Соотношения линейной теории упругости
- •Одноосного сжатия
- •6. Основы гидродинамики
- •6.1. Основные положения
- •Закон сохранения массы;
- •6.2.Закон сохранения массы
- •6.3. Закон изменения количества движения
- •6.4. Закон изменения момента количества движения
- •6.5. Закон изменения кинетической энергии
- •6.6. Закон сохранения энергии для контрольного объёма сплошной среды
- •6.7. Уравнения движения и равновесия
- •7. Теоретические основы решения одномерных задач
- •7.1. Основные термины и понятия
- •7.2. Уравнение бернулли для установившегося напорного потока вязкой жидкости
- •7.3. Геометрическая и энергетическая интерпретации слагаемых, входящих в уравнение бернулли
- •7.4. Потенциальный и полный (гидродинамический) напоры. Пъезометрическая и напорная линии
- •8. Основы реологии
- •8.1. Уравнения состояния идеальных и реальных жидкостей
- •8.2. Моделирование движения сложных сред
- •8.2.1. Течение ньютоновской жидкости в круглой трубе
- •8.2.2. Неньютоновские жидкости
- •8.2.3.Механические модели неньютоновских сред
- •9. Движение жидкостей и газов в пористой среде
- •9.1.Основные понятия
- •9.2.Определение эффективного диаметра
- •9.3.Формулы фильтрации
- •10. Базовые задачи гидродинамики, используемые в нефтегазовой отрасли
- •10.1. Постановка задач
- •10.2. Ламинарное и турбулентное течение жидкостей в щелевом канале
- •10.3. Ламинарное и турбулентное течение жидкостей в кольцевом канале
10.2. Ламинарное и турбулентное течение жидкостей в щелевом канале
Ламинарное течение ньютоновской жидкости. Согласно соотношениям Коши и уравнениям состояния при течении жидкости в щели, отличными от 0 будут лишь одна скорость деформации и одно напряжение сдвига (10.1.1):
Из уравнений состояния сохранится лишь одно, а именно
![]() .
(10.2.1)
.
(10.2.1)
Сравнивая это уравнение с решением (10.1.3)
![]() ,
,
получаем дифференциальное уравнение относительно скорости
![]() ,
,
решение которого при граничном условии v(h) = 0, (2h ширина щели) имеет вид
![]() .
(10.2.2)
.
(10.2.2)
Используя формулы (10.1.4), можно определять основные характеристики потока:
объёмный расход
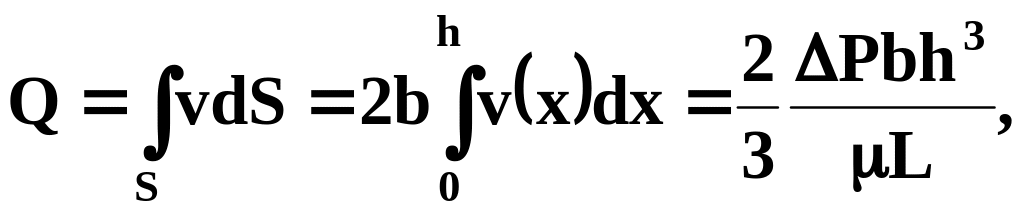
среднюю скорость


коэффициент сопротивления
 ,
,
где
S, S соответственно площади поперечного сечения и боковой смоченной поверхности канала;
f = / W коэффициент трения Фаннинга;
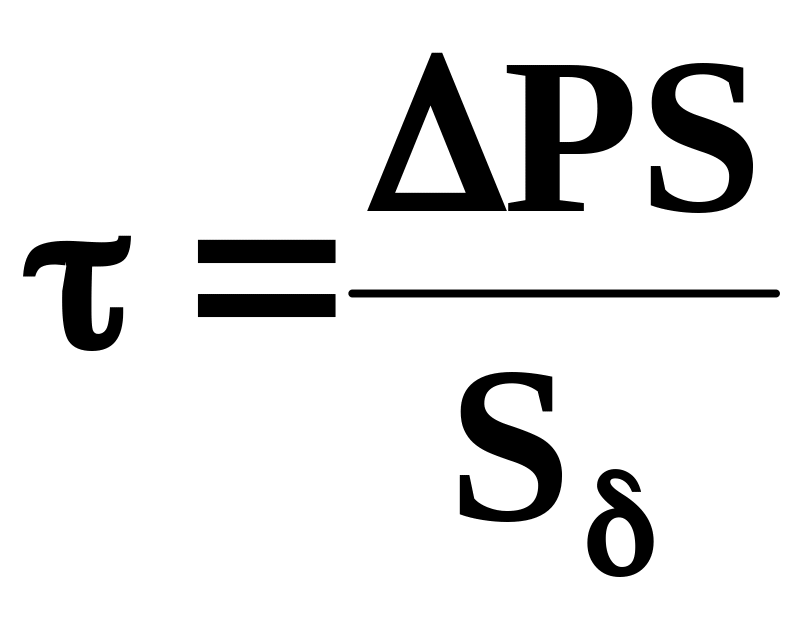 касательное
напряжение у поверхности канала;
касательное
напряжение у поверхности канала;

кинетическая энергия единицы объёма
жидкости;
кинетическая энергия единицы объёма
жидкости;
b длина поперечного сечения щели;
 параметр
Рейнольдса для плоской щели.
параметр
Рейнольдса для плоской щели.
Например: при = 1000кг/м3; vср = 1 м/с; 2h = 0,01 м; = 0,01Пас;
имеем: Reщ = 1000; = 0,048; P/L = 1200 Па/м. Таким образом, на каждые 1000 м гидравлические потери составят 1.2 МПа.
Ламинарное течение неньютоновской жидкости Шведова Бингама. Используя соотношение (5.1) и подставляя его в (1.87) интенсивность касательных напряжений и (1.88) интенсивность скорости деформации сдвига при скорости деформации объёма ( = 0), будем иметь:
![]() .
(10.2.3)
.
(10.2.3)
Знак
()
выбран из-за того, что
![]() .
.
Система уравнений упрощается до одного уравнения
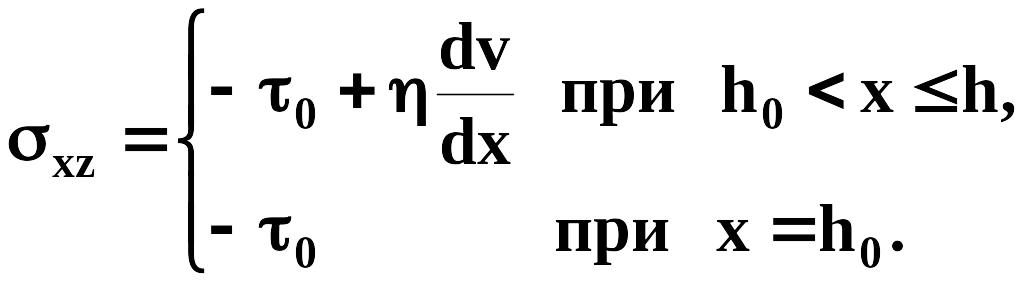 (10.2.4)
(10.2.4)
Сравнивая (10.2.4) с (10.1.3), получаем уравнение скорости
 (10.2.5)
(10.2.5)
и формулу для вычисления ядра потока
![]() .
(10.2.6)
.
(10.2.6)
Интегрируя уравнение (10.2.5) при v (h) = 0, найдём следующее распределение скорости:
![]() (10.2.7)
(10.2.7)
Отсюда следует:
при h0 = h движение жидкости происходить не будет, т.к. v (x) = 0;
условием существования движения является h0 < h или, используя формулу (10.2.6),
![]()
Если учесть, что начало движения рассматриваемой жидкости обусловлено не динамическим напряжением сдвига 0, а статическим 00 0, то условием страгивания покоящейся жидкости будет
![]() .
.
По формулам (10.1.4) определяют основные характеристики потока (впервые получены М.П. Воларовичем и А.М. Гуткиным):
 (10.2.8)
(10.2.8)
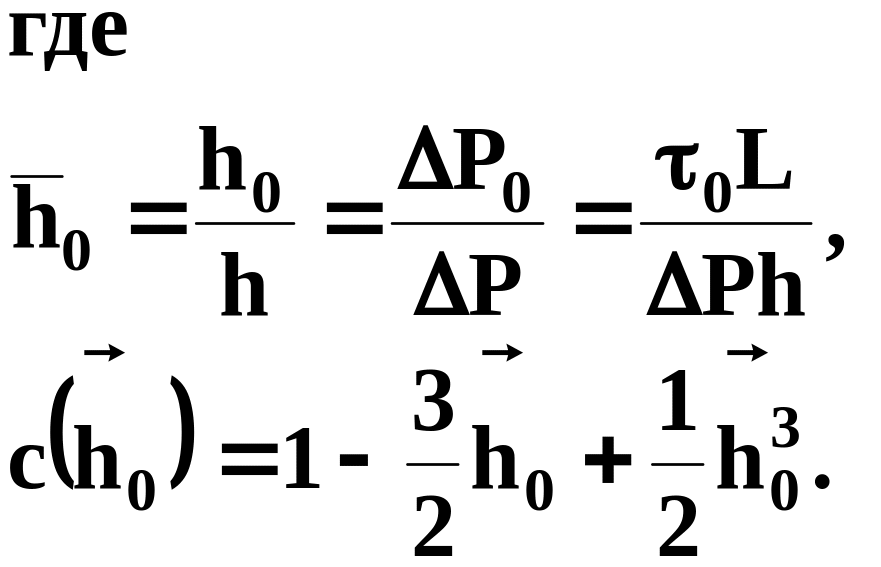
Как видно из полученных выражений, кинематические характеристики потока Q, vср и коэффициент сопротивления зависят от градиента давления нелинейно, что вызывает трудности при решении обратной задачи.
Если исходить из того, что практический интерес представляет случай, когда Р 0 (h0<<1), то, приняв c (h0) = 1 3/2h0, получим:
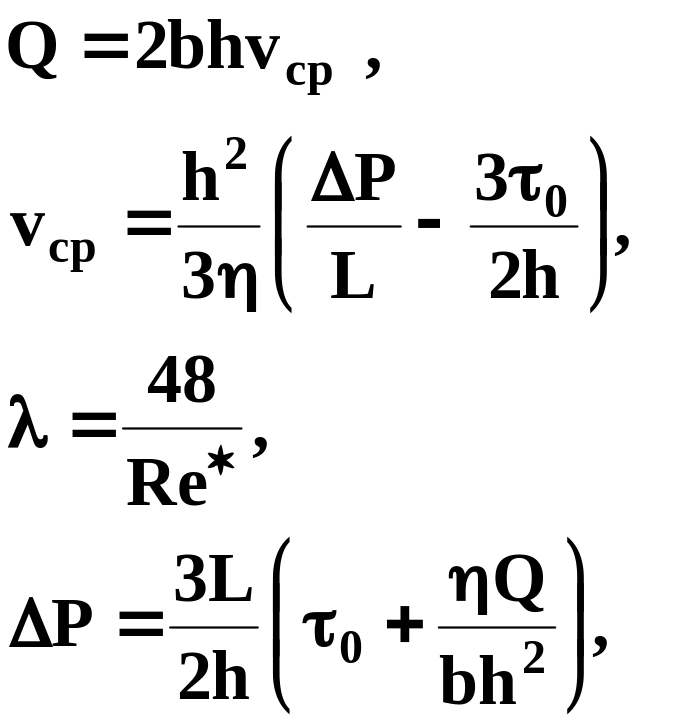 (10.2.9)
(10.2.9)
где
![]()
обобщённый параметр Рейнольдса;
=
(1+ 1/4Senщ)
приведённая вязкость жидкости Шведова
Бингама; Senщ
= 02h/vср
параметр Сен-Венана для плоской щели.
обобщённый параметр Рейнольдса;
=
(1+ 1/4Senщ)
приведённая вязкость жидкости Шведова
Бингама; Senщ
= 02h/vср
параметр Сен-Венана для плоской щели.
Например, при = 1350 кг/м3, 0 = 5 Па, = 0.04 Па с; vср = 1 м/с, h = 0.02 м. Получим:
![]()
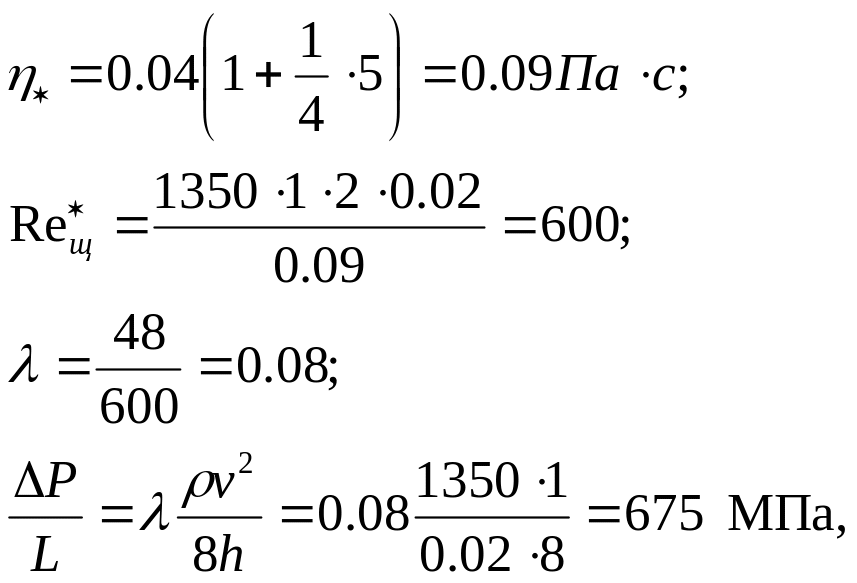
т.е. в этом случае на каждые 1000 м гидравлические потери составляют 0.675 МПа.
Неньютоновская жидкость Освальда Вейля. Используя в системе уравнений Коши соотношения (10.1.1) и (10.2.3)
 и
и
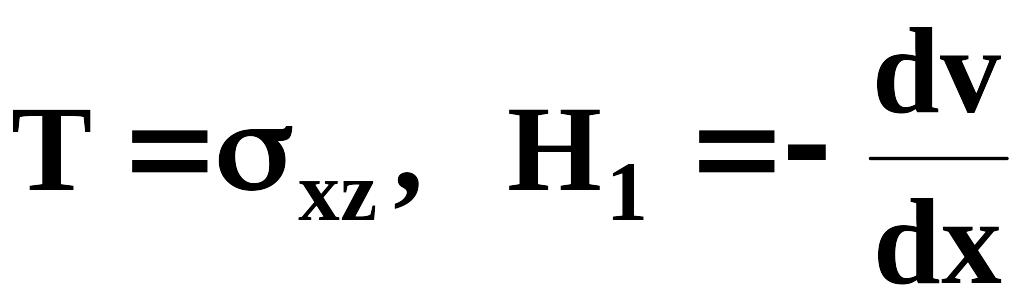 ,
,
получим
 .
.
Сопоставляя это уравнение состояния с решением (5.3), приходим
к дифференциальному уравнению относительно скорости:
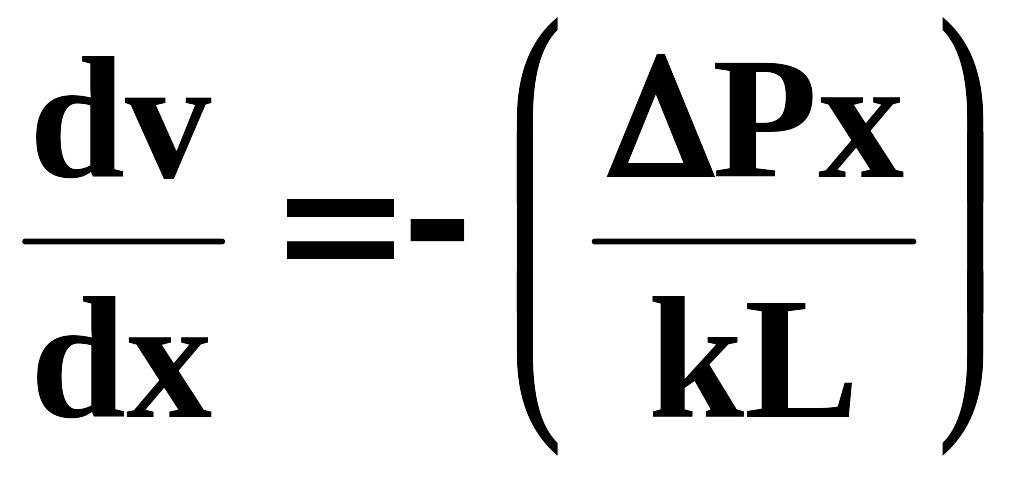 . (10.2.10)
. (10.2.10)
Интегрируя это уравнение при граничном условии v (h) = 0, получаем распределение скорости:
![]() , (10.2.11)
, (10.2.11)
где
![]() .
.
Интегральные характеристики потока при этом будут
![]() (10.2.12)
(10.2.12)
где
![]()
обобщённый параметр Рейнольдса,
обобщённый параметр Рейнольдса,
![]() приведённая
вязкость жидкости Освальда Вейля
для плоской щели.
приведённая
вязкость жидкости Освальда Вейля
для плоской щели.
При n = 1 и k = формулы (10.2.11) (10.2.12) совпадут с формулами (10.2.3) (10.2.4).
Турбулентный режим течения. Когда параметры Re, Re* или Re’ больше критических значений, решение уравнения движения записывается в виде (сравните с (10.1.3)
![]() .
.
Касательное напряжение ij в зависимости от типа жидкости связано со скоростью сдвига уравнениями вида (10.2.1), (10.2.3) или (10.2.10). Напряжение Рейнольдса в силу соотношений (10.2.3) удовлетворяет уравнению Прандтля:
![]() , (10.2.13)
, (10.2.13)
где принимается, что величина l линейно зависит от расстояния до стенки канала s = h х , т.е.
ℓ = æS (10.2.14)
где æ константа, определяемая из опыта.
Напряжение ij имеет существенное значение лишь в непосредственной близости от стенок канала, т.е. в узкой области, состоящей из ламинарного подслоя и буферной зоны, где ламинарные и турбулентные законы течения сравнимы между собой.
В основной области течения (турбулентное ядро) можно пренебречь напряжением. Поэтому после подстановки (5.17) и (5.18) в (5.16) получим следующее исходное дифференциальное уравнение:
![]() при s
s1
, (10.2.15)
при s
s1
, (10.2.15)
где = h/L – приведённое значение касательного напряжения; s1 – внешняя граница буферной зоны.
Упрощение
введено Прандтлем без какого-либо
физического обоснования, но большой
погрешности в решение не вносит. Если,
кроме того, ввести обозначение для
динамической скорости на стенке канала
![]() ,
то уравнение (10.2.15) примет вид
,
то уравнение (10.2.15) примет вид
![]() при s
s1
.
при s
s1
.
Интегрируя это
уравнение при условии
![]() ,
получаем универсальный закон распределения
скорости:
,
получаем универсальный закон распределения
скорости:
![]() при s
s1. (10.2.16)
при s
s1. (10.2.16)
Многочисленные экспериментальные подтверждения показали, что логарифмическое распределение (10.2.16) достаточно хорошо описывает профили скорости при турбулентных течениях различных жидкостей в плоских и круглых каналах с гладкими и шероховатыми стенками вплоть до больших значений параметра Рейнольдса (за исключением узких пристенных областей). Различия могут составлять лишь входящие параметры.
