6.3. Литература

1. Методические рекомендации к расчету водохранилищ-охладителей. ТЭС ПЗЗ — 75, ВНИИГ. Я., 1976. 97 с.

2. Указания по термическому расчету водо­хранилищ/Сост. А. И. Пехович, В. М. Жидких. ВСН 18 — 68, Минэнерго СССР. Л., 1969. 70 с;

3. ВСН 46 — 71, Минэнерго СССР. Л., 1972. 71 с.

4. Бибиков Д. И., Петруничев Н. В. Ледовые затруднения на гидростанциях. М.; Л., 1950. 159 с.

5. Готлиб Я- Л., Жидких В. М.;- Сокольников Н. М. Тепловой режим во­дохранилищ гидроэлектростанций. Л., 1976. 203 с.

6. Пивоваров А. А. Термика замерзающих водоемов. М., 1972. 140 с.

7. Российский К., И. Термический ре­жим водохранилищ. М., 1975. 167 с.

8. Константинов А. Р., Трушев­ский В. Л., Химии Н. М. Оценка влияния изъятия стока на тепловой режим про­точного водоема (постановка задачи). — В кн.: Гидрометеорологическое обеспечение народного хозяйства. Л., 1982, с. 112—118.

9. Годунов С. К, Рябенький В. С, Разностные схемы. Введение в теорию. М., 1977. 213 c$ 9. М а р ч у к Г. И. Методы вычислительной математики. М.,, 1977. 455 с.

10. Спицын И. П., Винников С. Д., Трушевский В. Л., Дивногорская Е. Ю. Балансовая модель термического режима устьевого взморья (на примере Обской губы). — Труды Арктич. и антарктич. науч.-исслед. ин-та, 1982, т. 378, с. 138—159.

11. Б р а с л а в с к и й А. П., Викулина 3. А. Нормы испарения с поверхности водохранилища. Л., 1964. 212 с.

12. А 1 b i-g n о t I. P., Boutin C, I s a k a H. Estimation du bilan thermique et de la temperature moyenne de la couche de melange d'un lac profond a l'aite de donnes meteorolo-giques de routine. — Archiv fur Meteorologie, Ge'ophysik und Bioklimatologie, Ser. A, 1979, Bd 28, N 1, p. 71—87.

7. Методические указания к практикуму «Расчеты тепломассопереноса в реках и водоемах»

7.1. Общие положения

Для практических расчетов разработаны разного рода схема­тизации задачи в виде частных моделей распространения неконсервативных примесей, солей и температуры. В основу решения этих моделей положены одномерные уравнения движения и неразрывности с применением операции осреднения по поперечным сечениям потока, к которым добавляются однотипные уравнения переноса тепла, кислорода и других субстанций. При решении задачи пе­реноса основное внимание уделяется определению значений вхо­дящих в уравнения переноса коэффициентов диффузии. В частности, коэффициентов тепло - и температуропроводности или кон­сервативности примеси. Вопрос определения этих коэффициентов затрудняется необходимостью исследования гидродинамики, например, требуется определение коэффициента турбулентной диффузии О.Ф. Васильев (1965, 1976) отмечает, что на достаточно большом расстоянии от места сброса тепла роль продольной дис­персии становится пренебрежительно малой, вследствие чего температура воды или концентрация примеси на этом расстоянии определяется главным образом адвективным переносом. Аналогич­ные выводы делал Д. Харлеман (1972) и др. Обычно принимается, что переносимое течением тепло не влияет существенным образом на плотность воды. Тогда в динамическом уравнении изменение плотности по длине водотока принимается равным нулю (так на­зываемое баротропное приближение). В этом случае уравнения Сен-Веннана решаются независимо от остальных, и затем полу­ченные результаты используются для решения уравнения переноса тепла. С помощью такого решения можно предсказывать распреде­ление температуры воды вдоль водотока, основываясь на данных о поступавшем водном и тепловом стоке в верхнем створе водотока и теплообмена с окружающей средой.

Пусть имеется информация о среднем установившемся уровне водоема и его ширине при отсутствии паводка. Для верхнего створа исследуемого объекта этот уровень можно при­нять за начало координат. Введем ось X , направленную вдоль оси водотока, ось Z направим вниз, а ось Y направим перпендикулярно плоскости XOZ c началом на оси водотока.

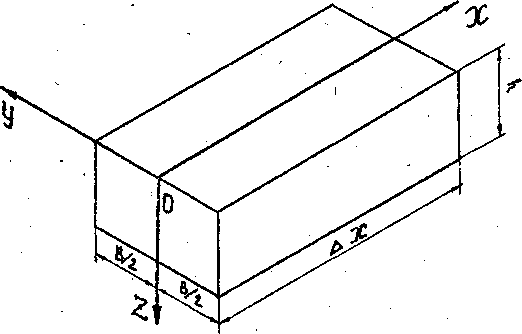
Рис.1. Принятая система координат.

Рассмотрим уравнение теплопроводности в заданных координатах в виде

(8)

Это уравнение получено в предложении, что перенос тепла в продольном направлении Х происходит, главным образом за счет течений,

(9)

а перенос тепла в вертикальном Z и поперечном Y направле­нии за счет турбулентной диффузии

(10)

(11)

Указание допущения в некоторой степени искажают истинную картину процесса теплопередачи, но в целом позволяют оценить основные физические закономерности. Например, первое допуще­ние позволяет пренебречь турбулентным тепловым потоком в про­дольном направлении. Этот вопрос специально рассмотрен А.П. Пеховичем (1972). Второе допущение подтверждается анализом большого числа натурных наблюдений и является общепринятым. Третье допущение позволяет в некоторой степени учесть теплоперенос в поперечном направлении, которым обычно вовсе пренебрегают.

Представление поперечных теплопотоков в виде правой части уравнения (8) является достаточно формальным. Коэффициенты и имеют смысл некоторых эффективных коэффициентов теплопроводности, хотя с физической точки зрения ничего общего с коэффициентами теплопроводности они не имеют. Однако с их помощью записывается общепринятая гипотеза о пропорциональности потока тепла градиенту температуры:

(12)

В реальных условиях тепловой поток обусловлен не только градиен­том температуры, но и множеством других факторов, подчас во­обще не поддающихся учету. Естественно, что в этих условиях величины и являются весьма изменчивыми в зависимости от гидротермических условий потока.

Важным требованием к моделям естественных процессов яв­ляется изменяемость всех входящих в них параметров. Величины и непосредственному измерению не подлежат. Измеряемыми являются профили температуры и величины теплопотоков. Преобразуем уравнение (8) таким образом, чтобы оно содержало лишь поддающиеся измерению величины теплопотоков на контурах, огранивающих водоток, для этого проинтегрируем его по сечению потока с учетом зависимости границ сечения от координаты X и времени . Результат интегрирования можно предста­вить в следующем виде

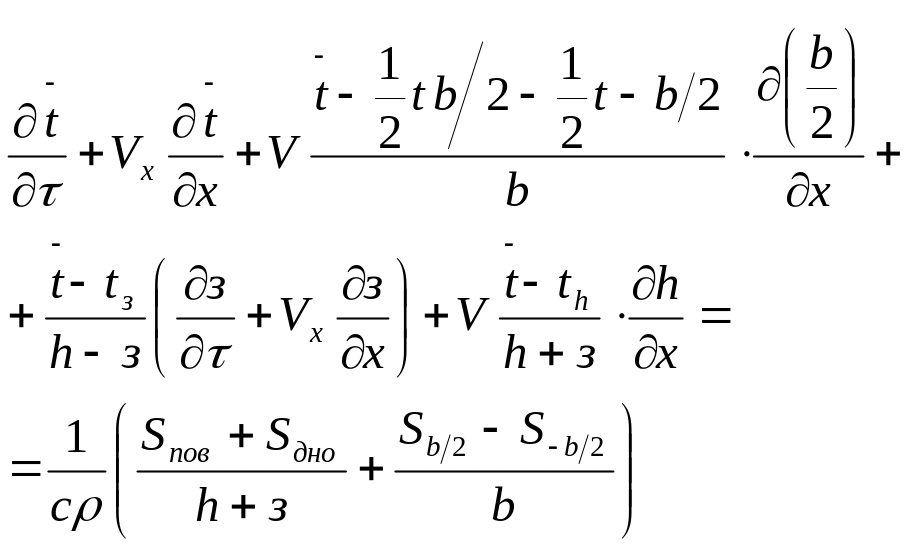
(13)

где: - средняя по поперечному сечению температура воды; - средние температуры поверхности и дна; и - температура на правом и левом берегу; ; - превышения уровня воды над равновесным; невозмущенная глубина потока (рис.2); - полуширина потока (ось направлена вдоль осевой линии потока); - величины удельных теплопотоков через горизонтальную, нижнюю, боковые поверхности водотока; - средняя скорость потока на сечении вдоль оси Х; - время; - удельная теплоемкость воды; - плотность воды. Величины и принимаются постоянными.

Рис.2

Уравнение (13) получено с помощью гипотезы (12). В это уравнение входят лишь величины, поддавшиеся непосредственному измерению ( ), либо величины, значе­ния которые могут быть вычислены с помощью надежных эмпиричес­ких формул ( ).

В большинстве случаев исследователя интересует главным образом, пространственно-временная изменчивость среднего по сечению теплосодержания водотока и температура его по­верхности . Поэтому, несмотря на то, что уравнение (13) является менее информативным по сравнению с уравнением (8), его точность является достаточной для практических расчетов. В методическом плане оно выгодно отличается (6) отсутствием не поддающихся определению величин и . Кроме того уравнение (13) является одномерным, что делает его легко интегрируемым.

Для замыкания уравнения (13) необходимо параметризировать профиль температуры по координате и . Запишем эту параметризацию в общем виде:

(14)

Вид функций (14) может быть определен либо из непосредст­венных наблюдений, либо продиктован соображениями здравого смысла. Например, при простейшей параметризации вида

(15)

уравнение (13) принимает вид

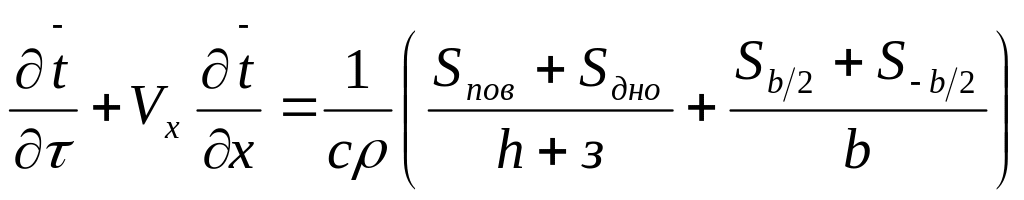(16)

Уравнение (16) необходимо дополнить краевыми условиями. На­чальное условие задаем в виде

(17)

Выбор граничных условий для уравнения гиперболического типа определяется типом течения. Если для всех , где - длина участка интегрирования, то достаточно задать условие, лишь на верхнем створе:

(18)

Если на нижнем створе имеет место инверсия потока , что может наблюдаться при прохождении нагонных волн, необходимо задать также условие на нижнем створе:

(19)

Система уравнений (13), (14), (17) - (19) является замкнутой. Такой подход может быть использован в системе уравнений движения и неразрывности или отдельно, когда известны значения V и . Кроме того, при достаточно малой скорости V или при её отсутствии уравнение (13) позволяет рассчитать термический режим водоема с учетом колебания уровня относи­тельно некоторой глубины по заданным .

Уравнение (13) является нелинейным благодаря нелинейной зависимости его правой части от температуры. Его решение возможно только численным методом.