5.2.2.4. Применение метода конечных разностей для решения уравнений кдп и пв

Для решения уравнений КДП и ПВ рационально использовать аппроксимацию уравнения в частных производных системой обыкновенных дифференциальных уравнений с использованием метода конечных разностей.

В настоящее время вряд ли можно предположить метод, который мог бы успешно конкурировать с методом конечных разностей при решении краевых задач описываемых уравнениями с частными производными, особенно в областях произвольной формы и с граничными условиями общего вида. Методу конечных разностей посвящено много работ. В работах [3, 8, 15] излагаются вопросы применения метода для уравнений с частными производными. Идея разностного метода заключается в замене производной ее приближенным значением, выраженным через разности значений функции в отдельных дискретных точках. Такая замена основана на применении ряда Тейлора [3, 10, 16].

Рассмотрим пример применения метода конечных разностей для исследуемого типа задач.

В связи с тем, что в подавляющее число модификаций общего уравнения конвективно-диффузионного переноса и превращения примесей входит выражение div (D · gradC), представим его в конечно-разностной форме.

1. Сетка с неодинаковыми шагами представляется в виде:

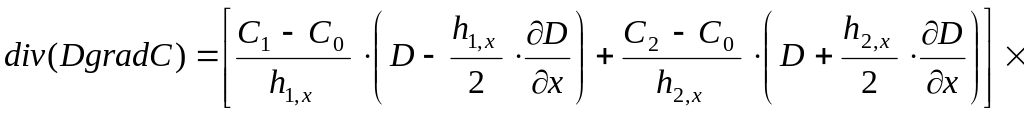
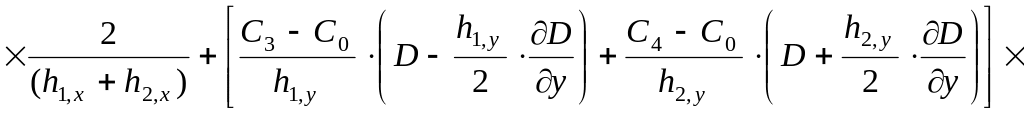
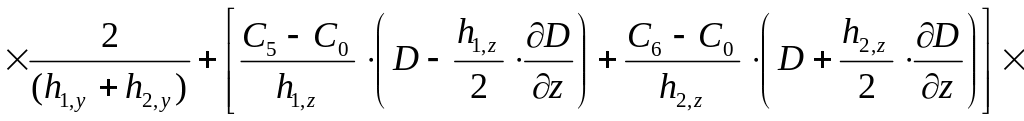
(2.18)

Эта формула имеет погрешность порядка h.

2. Сетка с одинаковыми шагами.

В ряде задач целесообразно применять равные шаги сетки для уменьшения погрешности численного решения задач. Поэтому обобщённый трёхразмерный лапласиан в разностной форме для сетки с одинаковыми шагами может быть представлен в виде:

Эта формула имеет погрешность порядка h2.

Рассмотрев выражения для коэффициентов перед разностями (Сm – C0)/h2m в формуле (2.19), нетрудно убедиться, что члены в скобках равны значениям D в точках, находящихся на расстоянии половины шага сетки выбранного нами узла. Погрешность такого представления имеет порядок h2. Тогда вместо (2.19) можно записать:

(2.19)

Приближённая замена одного дифференциального уравнения в частных производных системой обыкновенных дифференциальных уравнений получила в прикладной математике название «метод прямых».

(2.20)

Пусть необходимо найти решение дифференциального уравнения (2.20) используя аппроксимацию этого уравнения системой обыкновенных дифференциальных уравнений.

Решение u(x, y) уравнения (2.20) отыскивается для прямоугольной области 0 < x < a, 0 < y < b на контуре которой u(x, y) должно удовлетворять краевым условиям:

u(0, y) = ₁(y), u(a, y) = ₂(y), u(x, 0) = ₃(y), u(x, b) = ₄(y).

В соответствии с методом прямых в расчётной области проведём ряд горизонтальных прямых на расстоянии hy друг от друга. Пусть число проведённых прямых п. Решение исходного уравнения (2.20) справедливо для любой точки области, а, следовательно, и для любой из проведённых прямых.

Обозначим координату y, соответствующую j-й прямой через yj. Тогда, очевидно, для j-й прямой справедливы равенства:

, где uj(x) = u(x, yj),

, (2.21)

где uj - 1(x) = u(x, yj – 1), uj + 1(x) = u(x, yj + 1), f(x, yj) = fj(x).

Подставляя соответствующие выражения в уравнение (2.20), реализуем краевую задачу системой обыкновенных дифференциальных уравнений:

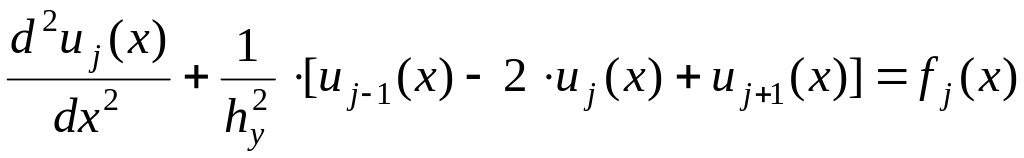, (2.22)

где j = 1, 2, 3, …, n. При этом u0(x) = 3(x), un+1(x) = 4(x).

Решением этой системы являются n функций одного переменного uj(x). В соответствии с (2.22) система обыкновенных дифференциальных

у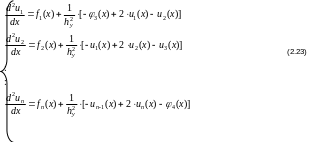 равнений имеет вид (2.23):

с начальными условиями:

(2.24)

u1(0) = 11, u2(0) = 12, …, un(0) = 1n,

u1(a) = 21, u2(a) = 22, …, un(a) = 2n.

Для решения этой системы краевые условия u1(ф) = 21, u2(a) = 22, …, un(a) = 2n необходимо пересчитать в неизвестные начальные условия u1’(0), u2’(0), …, un’(0).