1.4.2. Статистические оценки параметров распределения

Статистическое  оценивание  заключается  в  приближенном  опреде-

лении числовых характеристик генеральной совокупности по выборочным

данным.

Рассматривая x1, x2, …, xn ,  как независимые случайные величины x1,

x2, …, xn , можно сказать, что найти статистическую оценку неизвестного

параметра теоретического распределения – это значит найти функцию от

наблюдаемых случайных величин, которая и даёт приближенное значение

оцениваемого параметра.

Итак,  статистической  оценкой  неизвестного  параметра  теорети-

ческого  распределения  называют  функцию  от  наблюдаемых  случайных

величин.

Любую  такую  функцию  называют  статистикой. К  статистикам

относятся:  выборочное  среднее,  выборочная  ковариация,  эмпирические

функции распределения и плотности.

Сравнение эмпирического распределения с теоретическим

р а с п р е д е ле нием

Эмпирической функцией распределения  (функцией распределения

выборки) называют функцию F  ^*(x), определяющую для каждого значения

x относительную частоту события X < x.

Чтобы  определение  было  понятным,  рассмотрим  пример.  Пусть из

генеральной  совокупности  извлечена  выборка,  причем  x1  наблюдалось  n

раз, x2 –  n2 раз,  xk –  nk раз и ∑ni = n – объем выборки.

Наблюдаемые значения xi  называются вариантами. Числа наблюде-

ний – частотами, а их отношения к объекту выборки ni /n = Wi   –   отно-

сительными частотами.

Итак, по определению

^{F* (x) = n}x ^/  n,

где  nx  –  число вариант, меньших x ; n – объем выборки.

В отличие от эмпирической функции распределения выборки функ-

цию распределения вероятности F(x)   генеральной совокупности называ-

ют теоретической функцией распределения.

Различие между ними в том, что теоретическую функцию распреде-

ления генеральной   совокупности F(x) определяет вероятность события X

< x, а эмпирическая функция распределения выборки F^*(x) определяет от-

носительную  частоту  этого  же  события.  Из теоремы  Бернулли  следует,

что относительная частота события X < x, т. е. F^* (x) → по вероятности к

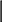
25

вероятности  F(x) этого события, и при больших n числа F^*(x)  и F(x) ма-

ло отличаются одно от другого в том смысле, что

 

n^{lim  Pх F x  F  x    1  0.}

Уже отсюда следует целесообразность использования эмпирической

функции распределения выборки для приближенного представления тео-

ретической функции распределения генеральной совокупности.

В ы б о р о ч н о е с р е д н е е и в ы б о р оч н а я д и с п е р с и я

Зададим  математическую  модель,  описывающую  свойства  иссле-

дуемой генеральной совокупности, в виде уравнения M (X, θ) = 0,

где x –  текущее значение случайного признака, причем X1, X2, …, Xn – вы-

борка из генеральной совокупности, любое значение которой xk = (x1, x2,

…,  xn)  получено  из  наблюдений;  θ  –  параметр,  значение  которого  надо

оценить по выборке.

Задача  математического  оценивания  θ  по  выборке  состоит  в  по-

строении такой функции от наблюдений, которая позволяет найти наибо-

лее точные (наилучшие) приближения для истинных значений θ.

Подобные наилучшие оценки могут быть получены по методу max.

правдоподобия и способу наименьших квадратов.

Для одномерной случайной величины x с неизвестной плотностью

f (x) параметр θ = (θ1,  θ2), где θ1 = M(x), θ2 = D(x).

Вся информация о параметрах θ1 и θ2 заключена в двух статистиче-

ских оценках:

 xk ,

x(n) 

1     ⁿ

ⁿ   k 1

(1.28)

где  ^x(n) - выборочное среднее арифметическое, которое при п → ∞ при-

ближается  согласно  закону  больших  чисел  к  М(Х)  -  математическому

ожиданию генеральной совокупности;

S  (n) 





xk2  x   ,

2

1     ⁿ

ⁿ  k 1

^( xk ^{ x(n)) 2 }

1

ⁿ     k

2

(1.29)

где S  ² (n) – выборочная дисперсия, стремящаяся при п → ∞ к генеральной

дисперсии D(X).

26

Для  того,  чтобы  статистические  оценки  давали  šхорошиеŸ

приближения оцениваемых параметров, они должны удовлетворять опре-

деленным требованиям.

Свойства оценок:

1. Свойство состоятельности. Оценка называется состоятельной,

если при п → ∞ она стремится по вероятности к оцениваемому значению

параметра, т.е. для сколь угодно малого ε > 0



P(/ θ   / ^  )  0  при п → ∞,



-

где   ѓЖ статистическая  оценка  параметра  θ.  Состоятельными  являются

оценки  ^х(n) , S²(n), Fn(X), fn(X).

2. Свойство несмещённости. Оценка является несмещённой, если

среднее  значение  при  любом  объеме  выборки  п  совпадает  с  истинным



значением параметра, т.е.  М    или  х  М ( Х ).



Если  М θ  θ , то оценка смещённая.

Параметры  нормального  закона  а  и σ²  являются  несмещёнными,  а

дисперсия (1.29) – смещённой.

3. Свойство эффективности. Эффективной называют статистиче-

скую оценку, которая (при заданном объеме выборки) имеет наименьшую

возможную дисперсию.

Лекция 2. Теория погрешностей измерений