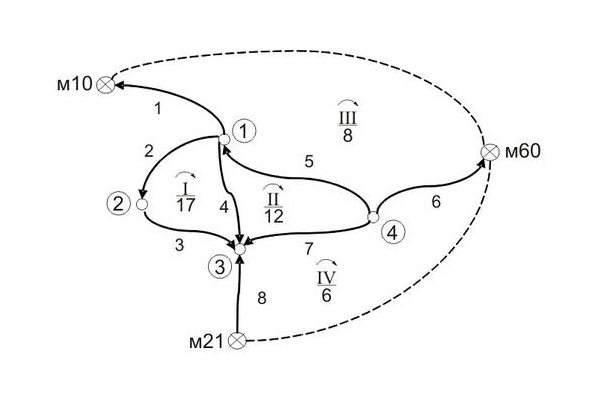
7. 1. Некоторые виды условий в геодезических сетях

Рассмотрим простейший пример уравнивания треугольника триан-

гуляции, в котором измерены все три угла.

^{В треугольнике образуется три исходных уравнения связи: х}1 ^= α1^;

^х2 ^= α2^;  х3 ^= α3  ^{и геометрическое условие суммы углов}

^α1 ^+ α2 ^+ α3 ^{= 180Ù. (7.1)}

Условие (7.1) из-за погрешностей измерений превращается  в усло-

вие

^α1 ^+ α2 ^+ α3 ^{= 180˚ + w, (7.1)}

^{где w = ∑ α} изм. ^{- 180˚  − невязка суммы углов треугольника.}

Если  в  измеренные  углы  ввести  поправки,  то  условие  (7.1)  будет

выполнено.  Поправки  определяются  в  результате  уравнивания  под  усло-

2

С  учетом  (7.1)  и  (7.2)  условное  уравнение  треугольника  можно

^{представить в виде v}1 ^+ v2 ^+ v3 ^{+ w = 0  или}

   ^¾ vi ^+ wj ^{= 0, (7.3)}

i j

^где vi ^{– поправка измеренных углов.}

56

В полигонометрическом ходе истинными условиями являются ра-

венство суммы углов

 ^{βi  ¾ 180˚ n = α  нач – α  кон (7.4)}

i

и сумм приращений координат

^{∑ Δх = х}  кон ^– х  нач ^{;  ∑ Δу = у}  кон ^– у  нач ^.

Из  условия  (7.4)  возникает  условное  уравнение  дирекционных  уг-

лов.

Для составления условных уравнений координат кроме измеренных

углов β и длин линий l вводят центральные координаты

τ =Х–  Χ ;  η = Y – ѓІ ,

где  ѓґ – ∑ Х/S;   ѓІ = ∑ Y/S;  S – число сторон.

Условные уравнения имеют вид

  ηi Vβi +  P ηнач δα нач –  P η  кон δα кон + δХн –

  ^{Vli Cos αi +}

S

1

P

S

1              1

P к

^– δХк ⁺

1

^η  Wβ ^+ Wх ^= 0;

  ^{Vli Sin αi –}

S

1

P

   ^{τi Vβi –}

S

1

P

^τнач ^δα нач ^–

1

P

^τкон ^δα кон ^+ δYн ^–

^– δYк ^–

1

P

^τк ^Wβ ^+ Wх ^{= 0.                                                                                (7.5)}

Максимальное  число  независимых  условий  равно  числу  избыточ-

ных измерений.

В разомкнутом нивелирном ходе

^wj ⁼  

^+ hi ^+ Hнач ^+ Нкон ^{,                            (7.6)}

i j

^где wj ^{– невязки условных уравнений или просто невязки.}

В замкнутом нивелирном ходе

^wj ⁼  

i j

^+ hi^.

57

Значения свободных членов условных уравнений не должны выхо-

дить за пределы технических допусков.

Допустимое значение невязки уравнения фигуры

^wдоп ^{≤ 2 m √3.}

Для условных уравнений дирекционных углов

^wдоп ^{≤ 2 m √n,}

где m – СКП измеренного угла; n – число углов, используемых в условии.

7. 2. Теория уравнивания коррелатным способом

Пусть в некотором геодезическом построении имеется n элементов

^х1^, х2^{, ...  , х}n ^{, измеренные значения которых составляют ряд l}1^, l2^, … , ln

^{c весами p}1^,  p2^, … , pn ^.

Здесь исходная система уравнений связи

^xi ^= li ^{,  i = 1, 2, …, n  (в матричном виде EX = L). (7.8)}

^{В этой системе каждому искомому элементу x}i ^{соответствует один}

^{измеренный элемент l}i ^.

^{С учетом погрешности измерений  x}i ^– li ^= vi^{. Число таких уравне-}

ний будет n.

^{Между  истинными  значениями x}i  ^{существует  зависимость  в  виде,}

например, нелинейной функции

^F (х1^, х2^{, ...  , х}n^{) = 0. (7.9)}

Приведем функцию к линейному виду, разложив ее в ряд Тейлора

dF

n

i1

^{Fj (х1, х2, ...  , хn) +   dx}i

^(xi  ^–  li ^{) = 0,                     (7.10)}

58

где j – число избыточных измерений.

^{Введя обозначения F}j ^(х1^, х2^{, ...  , х}n^) = wj ^и

dF

^dxi

^= ai^, + bi^, +

[v ] = min  (для равноточных измерений)  или  [pv ] = min  (для неравно-

^{+ … + ,  q}i^{,  получим систему условных уравнений поправок}

^a1 ^v1 ^+  a2 ^v2 ^+ … + an ^vn ^+ w1 ^= 0;

^b1 ^v1 ^+  b2 ^v2 ^+ … + bn ^vn ^+ w2 ^= 0;

… … … … … …

^q1 ^v1 ^+  q2 ^v2 ^{+  … + q}n ^vn ^+ wr ^{= 0. (7.11)}

Поправки должны удовлетворять принципу наименьших квадратов

2 2

точных измерений). В матричном виде

V ^Т Р V = min. (7.12)

Система (7.11) в матричной записи

BV + W = 0,

где составляющие матрицы равны

^а  1 ^а  2

^а  п

^v  1

^w 1

В=

^b 1 ^b  2

^b

п

V=

^v  2

W=

^w  2

.    (7.13)







^q  1 ^q  2

^q

n

^v  n

^w  n

^{Система уравнений (7.11) неопределенная, т.к. число v}i ^{всегда боль-}

ше r – числа уравнений.

Для решения системы под условием (7.12)   находят относительный

минимум функции Л а г р а н ж а

^{2Ф = [pv2] – 2K}1 ^([av] + w1^{)  – … – 2K}r ^([qv] + wr^),

При t = Е, т.е. равноточных измерениях, V = B  K.

59

^{где 2Ф – условная запись квадратичной формы, в которой К}1^, К2^{, ... , К}r ^–

неопределенные множители Лагранжа, называемые коррелатами.

В матричной форме функция имеет вид:

2Ф = V^T P V – 2K ^Т (BV + W) = min.

Представив функцию в развернутом виде, взяв от нее частные про-

изводные по каждой поправке vi  и приравняв их к нулю, после несложных

преобразований получим систему  к о р р е л а т н ы х у р а в-

нений поправок

^vi ^= ti ^ai ^K1 ^+ ti ^bi ^K2 ^+ … + ti ^qi ^Kr ^{, (7.14)}

^{в которой t}i ^= 1/рi ^{– обратные веса измерений.}

В матричной записи система коррелатных  уравнений поправок бу-

дет

V = P  ^-1 B^T K = t B^T K.

T

Для определения коррелат составляют нормальные уравнения путем

^{подстановки v}i ^{(7.14) в условные уравнения (7.11).}

Система  н о р м а л ь н ы х у р а в н е н и й к о р р е л а т  имеет вид

^[taa] K1 ^+ [tab] K2 ^{+ … + [taq] K}r ^+ w1 ^= 0;

^[tab] K1 ^+ [tbb] K2 ^{+ … + [tbq] K}r ^+ w2 ^= 0;

… … … … …

^[taq] K1 ^+ [tbq] K2 ^{+ … + [tqq] K}r ^+ wr ^{= 0. (7.15)}

В матричной записи:

B t B^T K + W = 0   B B^T K + W = 0,

где K = - Q W,  а Q = (B t   -1 B )

T -1

– обратная матрица нормальных

уравнений, элементы которой находятся по схеме Гаусса.

Нормальные уравнения составляют по установленным схемам (таб-

личный вариант).

Найденные в результате решения коррелаты подставляются в урав-

нение (7.14).

После ввода поправок в измеренные значения получают уравненные

значения.

60