6. 2. Способ узлов Попова составления нормальных уравнений.

Для уравнивания нивелирных сетей и углов в сети полигонометрии

профессор  В.В.  Попов  предложил  следующие  правила  составления  нор-

мальных уравнений с помощью схемы сети (рис. 6.1):

 квадратичные коэффициенты нормальных уравнений в строке с

номером  j – м  равны сумме весов тех ходов, которые сходятся

в узловом пункте с номером  j – м;

 неквадратичные коэффициенты нормальных уравнений в стро-

ке с номером  j – м  и столбце с номером  k – м  равны весу хо-

да, соединяющего узлы с номерами   j – м   и   k – м,   взятому со

знаком  š − š.

 свободные члены нормальных уравнений получают суммирова-

нием величин   ^Ä pi li  тех ходов, которые сходятся в узле   j – м,

причем, если узел является конечной точкой  хода, то ставится

знак  š + š, а если начальной, то š – š.

Пример:

Схема  нивелиной  сети

А

1

II

3

В

2

I

5

7

4 III С

6

Рис. 6.1

Квадратичные коэффициенты: [paa] = p1 + p2 +  p4 ; [pbb] = p2 +  p3 +

+ p5 +  p7 ;  [pcc] = p4 + p5 +  p6 .

Неквадратичные коэффициенты: [pab] = - p2 ; [pac] = - p4 ;

[pbc] = - p5 .

49

Свободные члены:  b1 = p1 l1 – p2 l2 – p4 l4 ;

b2 = p2 l2 + p3 l3 – p5 l5 + p7 l7 ;

b3 = p4 l4 + p5 l5 – p6 l6 .

В результате получим систему уравнений

(p1 + p2 +  p4) δx1 - p2 δx2 - p4 δx3 + b1 = 0

- p2 δx1 + (p2 + p3 +  p5 + p7) δx2 - p5 δx3 + b2 = 0

- p4 δx1 - p5 δx2 + (p4 + p5 +  p6) δx3 + b3 = 0

6. 3. Виды уравнений поправок

Рассмотрим основные. Наиболее простой вид они имеют в нивелир-

ных сетях.

В нивелирных сетях для каждого i – го   превышения исходное урав-

нение связи имеет вид

Yi = Xкон –  Хнач = f (X), (6.13)

где Хн  и Хк – истинные значения высот начальной и конечной точек хода

(между узловыми пунктами).

Уравнение поправок будет

vi = δхкон –  δхнач +  li . (6.14)

Свободный член  li = f (Х^о) – yi = Хк^о – (Хн^о + yi).

Коэффициенты параметрического уравнения поправок будут

ai = (dYi / dXкон)o = 1;  bi = (dYi / dXнач.)o = -1.

Если ход опирается на исходный пункт, то либо δxнач. = 0, либо

δxкон = 0.

Х^о,Y^o – приближенные значения высот узловых пунктов.

Δx – поправки к приближенным значениям.

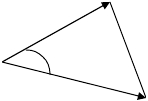
В сетях триангуляции измеряют направления (стороны) и углы

(рис. 6.2).

Уравнение поправок для измеренного угла легко получить как раз-

ность уравнений поправок для дирекционных углов.

50

k

i ^β

s

j

Рис. 6.2

Так как

^βkj ^= αij ^- αik , ^то  v  ^β= v ^αij ^- v ^αik ^+ l ,

^{где  l = l α}ij ^- l αik ^.

(6.17)

В матричной форме

^vi ^{= Aik δk + (Aik - Aij ) δi - Aik δj + li .}

Для стороны  S, измеренной между пунктами  j – м  и  k – м , исход-

ное уравнение связи имеет вид   S = (Xk – Xj)² + (Yk – Yj)².

Найдем коэффициенты уравнений поправок:

ai = (dS /dXj)o = - cos αjk^o ; bi = … = - sin αjk^o ;  ci = … = cos αjk^o ;

di = … = - sin αjk^o ,

где   αjk^o –  приближенный  дирекционный  угол стороны,  вычисленный  по

координатам  Xj^o, Yj^o, Xk^o, Yk^o.

Свободный член  l =  S^o – Sj'k = (Xk^o – Xjo)² + (Yk^o – Yj^o)² –  Sj'k ,

где  Sj'k  − измеренная сторона.

Окончательное уравнение поправок для  i-ой стороны

Vi = – cos αi^o δxj –  sin αi^o δyj + cos αi^o δxk + sin αi^o δyk + li . (6.18)