4.2.Оценка точности функций геодезических измерений

В  рассматриваемых  выше  примерах  горизонтальные  проложения,

приращения  координат,  координаты  являются  функциями  от  измеренных

величин

y = f (x1, x2, … , xn), (4.1)

где  xi  –  аргументы  функции  f,  которые  как  результаты  измерений  могут

быть равноточными и неравноточными, зависимыми (коррелированными)

и независимыми.

Результаты измерений xi содержат погрешности, поэтому их оценка

точности  заключается  в  определении  средних  квдратических  погрешно-

стей.

Также и функция y = f (xi) будет содержать среднюю квдратическую

погрешность my, которую необходимо определить.

Для получения оценки точности функции "у" находят сначала ее ис-

тинные погрешности, используя разложение исходной зависимости (4.1) в

ряд Тейлора

n

^{Δy = f (x1, x2, … , xn) +}    ^{Fi' Δi , (4.2)}

i1

где x1, x2, … , xn – результаты равноточных измерений;   Fi' = df (x1, x2, … ,

xn) / dxi – частные производные; Δy – истинная погрешность функции; Δi -

истинная погрешность аргумента.

Вычтя из выражения (4.2) функцию (4.1), получим

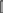
40

n

^Δy =    ^{(df / dxi) Δi , (4.3)}

i1

т. е. в первом приближении истинная погрешность функции равна линей-

ной комбинации истинных погрешностей прямых измерений xi .

Используя свойства корреляционных моментов (Ki j –   корреляцион-

ный момент,  характеризующий  тесноту корреляции), находим дисперсию

истинной погрешности функции (Δy)

σ   + 2   

n

^σ2y ^= 

i 1

Fi ^' 2

2

i

i1        ji1

n             n

Fi' Fj'  KΔi Δj .                     (4.4)

Однако значение корреляционного момента зависит еще и от рассе-

янности случайных  величин, которую  в чистом виде определяет  коэффи-

циент корреляции   ri j = Ki j / σi σj . Коэффициент корреляции изменяется в

пределах -1 ≤ r ≤ 1. Если случайные величины Xi и Xj  независимы, то

Ki j = 0 (также и ri j = 0 ).

Для некоррелированных погрешностей

n

 i1

^σ 2y ^=  

^σ2i  ^Fi' ^{2.                                      (4.5)}

Переход   к дисперсии функции (4.4) соответствует в теории погреш-

ностей переходу к квадрату СКП my2, т.е. к выражению

n

my  = 

2

i1

^(df / dxi^)2 mi^2 + 2 

i j

(df / dxi) (df / dxj) ri j mi mj ,           (4.6)

где ri j  mi  mj  ≈  lim [Δi  Δj ] / n, при n → ∞.

Таким образом, СКП функции (4.1) коррелированных измерений (ар-

гументов) определяют по формуле

 (df / dx) 2 mi2 + 2 ji

^m y ^

n

i 1

(df / dxi) (df / dxj) ri j mi mj .             (4.7)

При некоррелированных измерениях формула (4.7) будет (ri j = 0)

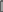
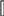
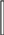
41

n

^my =  ^(df

^/ dxi ^)2 mi ^2,

(4.8)

i 1

т.е. СКП функции общего вида равна корню квадратному из суммы произ-

ведений квадратов частных производных функции по каждой переменной

на квадрат ее СКП.

Формулы  (4.7)  и  (4.8)  полностью  решают  задачу  оценки  точности

функций общего вида.

Оценку точности любой другой функции рассматривают как частный

случай оценки точности функций общего вида.

Для функции у = х1 ¾  х2

^my =   m1^2  m2^2 .

При m1 = m2 = m

my = √ 2.

Для функции у = k x

my = k mx,

где k – постоянная величина (безошибочное число), а х – аргумент, полу-

ченный со случайной погрешностью Δх .

Обобщая формулу у = k x   для случая многих аргументов у = k1 x1 ¾

...  ¾  kn xn получаем

n

^m  y   ^

^ k  i^2 m  i²

.

i 1

В случае k1 = k2 = … = kn ;  m1 = m2 = … = mn

my = k m √ n .

Эта формула отвечает оценке точности функции у = х1 ¾ х2  ¾ ...  ¾  xn.

В случае неравноточных измерений каждое значение xi имеет вес Рi

Задача – определить вес функции Ру .

Основываясь на общей формуле определения веса и формулах (4.7) и

(4.8) найдем формулу для обратного веса функции:

от коррелированных измерений

42

n

1/ру =

^i   1

^(df / dxi^)2 + 2 

i j

(df / dxi) (df / dxj) ri j / Pxi  Pxj ;           (4.9)

от некоррелированных измерений

n

^1/ру =  

(df / dxi)²  1 / Pxi .                                       (4.10)

i1

Примеры:

1. Измерена линия S  со средней квадратической погрешностью ms  и

угол наклона ν со средней квдратической погрешностью mν . Определить

среднюю квдратическую погрешность  превышения  h = S ∙ Sin ν.

По формуле (4.10) найдем

^mh  ^{ Sin2ν  m}S^{2  S2  Cos 2ν  m}^2 / ρ2 ,

где Sin ν = dh/ds ;  S Cos ν = dh/dν ; ρ = 206 265" .

2. Два угла треугольника измерены каждый с Р = 1. Определить ве-

роятность третьего (Р3) вычисленного угла.

γ = 180^Ù - (α + β). Если известны СКП mα  и mβ , то m2γ = m2α  +  m2β .

Согласно формуле (4.10) заменим квадрат СКП обратными весами

1/Рγ = 1/Рα + 1/Рβ .

Учтя, что Рα = Рβ = 1, получаем 1/Ру = 2, а Ру = 1/2.

Лекция 5. Уравнивание геодезических измерений.

Метод наименьших квадратов