1.2.2. Законы распределения случайных величин

В силу того, что повышение точности измерений имеет ограничен-

ные возможности, в практике геодезических измерений используют дис-

кретную случайную величину.

Для  задания  дискретной  случайной  величины  кроме  перечисления

всех возможных ее значений, нужно указывать их вероятности.

Соотношения, с помощью которых устанавливают связь между воз-

можными значениями случайной величины и соответствующими им веро-

ятностями  (Р),  называют  законом  распределения  дискретных  случайных

величин. Он может быть задан: таблично, аналитически, графически.

Таблично:

В первой строке таблицы возможные значения случайной величины,

а во второй – их вероятности.

События первой строки образуют полную группу событий, следова-

тельно

∑рi = 1.

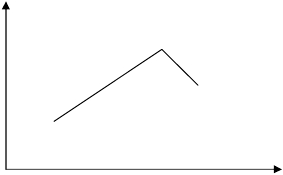
Графически: В прямоугольной системе  координат строят точки  (хi,

рi) и соединяют их отрезками прямых (рис. 1). Полученную фигуру назы-

вают многоугольником распределения.

9

Pn(q)

Х

x1 x2 x3 x4

Рис. 1

Примером  аналитического  выражения  закона  распределения  для

прерывных случайных величин может служить вероятность появления со-

бытий k раз при n испытаниях, т. е. формула Бернулли

Pn(k) = Cnk p  ^k q  ^n-k, (1.1)

где k = 0, 1, 2, … , n; Cnk – сочетание из n элементов по k элементов; p  ^k –

вероятность появления события k раз; q  ^n - k – вероятность непоявления со-

бытия n-k раз.

Распределение вероятностей, определяемое формулой Бернулли, на-

зывается Биноминальным.

Пример. Монета брошена два раза. Написать в виде таблицы закон

распределения случайной величины Х – числа выпадений šорлаŸ.

Решение.  Вероятность  появления  šорлаŸ  в каждом  бросании  равна

1/2, а вероятность не появления q = 1-1/2 = 1/2. Возможные значения Х: х1

= 2; х2 = 1; х3 = 0. Найдем вероятности этих возможных значений по фор-

муле Бернулли:

p2(2) = c22 p² = (0,5)² = 0,25;

p2(1) = c21 p q = 2 ∙ 0,5 ∙ 0,5 = 0,5;

p2(0) = c20 q² = (0,5)² = 0,25.

Напишем искомый закон (зададим) таблично.

Контроль: 0,25 + 0,5 + 0,25 = 1.

10

Когда n велико, а p мало, для определения вероятности k появлений

события  в  испытаниях  пользуются  формулой  Пуассона,  отсюда  закон  –

закон распределения Пуассона.

Pn(k) = λ  ^k e^-λ / k!, (1.2)

где e – основание натурального логарифма; λ = n∙ р – постоянная величина

(среднее число появлений события в различных сериях испытаний – при

различных значениях n, остается неизменным); ! – т. к. опущен знак при-

ближенного равенства ≈.

Есть специальные таблицы, по которым можно найти Pn(k), зная k

и λ.

1.2.3. Функция распределения вероятностей

случайных величин

Если  дискретная  случайная  величина  может  быть  задана  перечнем

всех её возможных значений и их вероятностей, то для непрерывных слу-

чайных величин этот способ неприменим.

Поэтому применяют общий способ задания любых типов случайных

величин.  Вводят  функции  распределения  вероятностей  случайных  вели-

чин.

Функцией распределения  называют функцию F(x), определяющую

вероятность того, что случайная величина Х  в результате испытания при-

мет значение, меньшее х, т. е.

F(x) = Р(Х < x). (1.3)

Иногда  вместо  термина  šфункция распределенияŸ используют тер-

мин šинтегральная функцияŸ.

Свойства функции распределения:

С в о й с т в о  1. Значения функции распределения принадлежат от-

резку [0, 1]:

0 ≤ F(x) ≤ 1.

С в о й с т в о  2. F(x) – неубывающая функция, т. е. F(x1) ≥ F(x1), ес-

ли x2 > x1.

Следствие  1.  Вероятность  того,  что  случайная  величина примет

значение,  заключенное  в  интервале  (а,  в),  равна  приращению  функции

распределения на этом интервале

Р(а ≤Х < в) = F(в) - F(а).

11

Следствие  2.  Вероятность  того,  что  случайная  величина  Х  примет

одно определенное значение равна нулю

Р(Х =  x1) = 0.

С в о й с т в о  3. Если возможные значения непрерывной случайной

величины  расположены  на  всей  оси  x,  то  справедливы  следующие  пре-

дельные соотношения:

lim F(x) = 0; lim F(x) = 1.

x → - ∞ x →∞

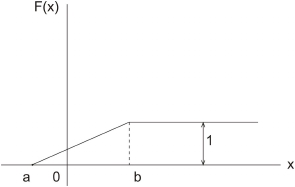
Свойства  позволяют  представить,  как  выглядит  график  функции

распределения непрерывной случайной величины (рис. 1. а).

График  расположен  в  полосе,  ограниченной  прямыми  у  =  0,  у  =  1

(первое свойство).

При возрастании х в интервале (а, в), в котором заключены все воз-

можные значения случайной величины, график šподымается вверхŸ (вто-

рое свойство).

При  x  a   ординаты  графика  равны  нулю;  при  x  b   ординаты

графика равны единице (третье свойство).

Рис. 1.а. График функции распределения непрерывной

случайной величины

График  функции   распределения  дискретной  случайной  величины

имеет ступенчатый вид (рис. 1. б).

12

Рис. 1.б. График функции распределения дискретной

случайной величины