1.3.2. Нормальный закон распределения

Плотности  распределений  непрерывных  случайных  величин  назы-

вают  также  законами  распределений.  Часто  встречаются  законы  равно-

мерного, нормального и показательного распределения.

Ч и с л о в ы е х а р а к т е р и с т и к и н е п р е р ы в н ы х с л у ч а й н ы х величин

Математическим ожиданием непрерывной случайной величины X,

возможные значения которой принадлежат отрезку [a, b], называют опре-

деленный интеграл

b

^{M ( X ) }  ^{xf (x)dx . (1.12)}

a

По аналогии с дисперсией дискретной случайной величины опреде-

ляется и дисперсия непрерывной случайной величины

b

^{D( X ) }  ^{[ X   M ( X )]2 f ( x)dx .}

a

(1.13)

Среднее  квадратическое  отклонение  непрерывной  случайной  ве-

личины определяется, как и для дискретной, равенством

17

σ(X)    D(X).

(1.14)

Свойства математического  ожидания и  дисперсии дискретных слу-

чайных величин сохраняются и для непрерывных.

Нормальное р а с п р е д е л е н и е

Нормальным называют распределение вероятностей  непрерывных

случайных величин, которое описывается плотностью

1

e

f(x) 

(x a)²

2σ ²

σ   2                         ^.

(1.15)

Из  формулы  видно,  что  нормальное  распределение  определяется

двумя параметрами: а и σ. Достаточно знать эти параметры, чтобы задать

нормальное  распределение.  Можно  доказать,  что  вероятностный  смысл

этих параметров таков:

М(Х) = а, т.е. математическое ожидание нормального распределения

равно параметру а;

σ(Х) = σ, т.е. среднее квадратическое отклонение   нормального рас-

пределения равно параметру σ.

Нормальное распределение с произвольными параметрами а и σ

(σ > 0) называют общим, а с параметрами а = 0 и σ = 1 – нормированным.

Плотность нормированного распределения

е х 2 .

( х) 

1

2

2

(1.16)

Эта функция табулирована.

После ввода новой переменной  z = (   x – a)/ σ   функция F(х) обще-

го нормального распределения

F ( x) 

1

   2

x

 ^e



(za)

2

2 ²

^dz ,                             (1.17)

а функция нормированного распределения

18

^F0 ^( x) 

1

2

x

 ^e



 z ²  2

^dz .

(1.18)

Эта функция также табулирована. Легко проверить, что

^{F ( x)  F}0 ^{(( x  a)  .}

Вероятность  попадания  нормированной  нормальной  величины  Х  в

интервал (0, х) можно найти, пользуясь формулой Лапласа

F ( x) 

1

2

x

^0 ^e

 z

2

2

^dz .

x

^{P(0  X  x) }  ^{ (x)dx  (x) .}

(1.19)

0

Можно получить F0(x) = 0,5 + Ф(х).

Вероятность попадания в заданный интервал нормальной случайной

величины

P(α  x  β)  (

β  a

σ

)  (

α  a

σ

).

(1.20)

Пример. Случайная величина Х распределена по нормальному зако-

ну.  Математическое  ожидание  и  среднее  квадратическое  отклонение  её

соответственно равны 30 и 10. Найти вероятность того, что Х примет зна-

чение в интервале (10, 50).

Решение. По формуле (1.20). По условию: α = 10, β = 50, а = 30,

σ = 10.

P(10  x  50)  (

50  30

10

10  30

)  (

10

)  2(2).

Ф(2) находят по таблице.

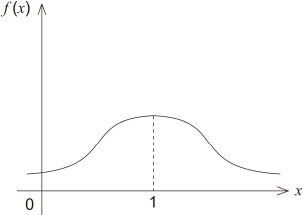
График плотности нормального распределения называют нормаль-

ной кривой (кривой Гаусса), рис. 1.3.

19

Рис. 1.3

а =1

σ=2

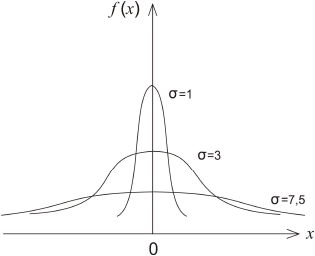
Влияние   параметров  нормального  распределения  на  форму  нор-

мальной кривой характеризует рис. 1.4.

Рис. 1.4

а = 0, если а любое, то нормальная кривая сдвигается по оси х.

При σ = 1 кривая называется нормированной.