6.1. Теоретические основы параметрического способа

уравнивания

Идея  параметрического  способа  уравнивания  изложена  в предыду-

щей лекции (сущность и способы уравнивания), где показано, как прямые

измерения связаны функционально с определяемыми параметрами.

Рассмотрим параметрический способ уравнивания в общем виде.

(df  i /dX  k )x  k = x o  = q   i ;  l  i = f  i (X  , X  , … , X  ) − y i .

45

Пусть известна исходная функция  f  связи между неизвестными па-

^{раметрами  Х} j  ^{и вектором измерений Y}

^f (X1^, X2^{, ...  , X}  ^{) = Y. (6.1)}

Вектор Y могут  составлять  как  измеренные  величины,  так  и  их

функции (дирекционные углы, координаты, высоты др.). Задача уравнива-

ния состоит в том, чтобы найти такие значения  x  параметров  Х,  которые

были бы наилучшими оценками.

^{По условию (6.1) каждому измеренному элементу   y} i  ^{соответствует}

^{элемент  f}  i  ^{, где i = 1,2, … , n  (n >k). Если предположить (для общности)}

неравноточность  измерений,  то  вектору   Y   будет  отвечать  вектор  весов

diag P.

Для  приведения  (6.1)  к  линейному  виду  надо  ее  разложить  в  ряд

Тейлора, для чего найти вектор приближенных значений неизвестных

^X 0j  ^= (X 1^0 , X 02 ^{, … , X 0}k ^{), используя результаты измерений. После нахожде-}

^{ния элементов (df} i ^/dx j ⁾  xjx⁰ j  ^{− частных производных функции   f   по пе-}

ременной  Х, запишем функцию в линейном виде

^(df i ^/dx j ⁾ xjx⁰ j  ^δx j ^+ f i ^( X 1^0 , X 02 ^{, … , X 0}k ^) = y i ^{, (6.2)}

^где δx j^= Х j ^− X 0j  ^{- поправка, равная разности между истинным и прибли-}

женным значениями искомого параметра.

o 0

^{Введем обозначения (df i /dX 1 )x 1 = x}1 ^{= a i ;   (df i /dX 2 )  x2  x2  = bi ;  … ;}

0 0 0

1 2 k

k

Тогда вместо (6.2) имеем

^a  i  ^δx 1   ^+ bi ^δx 2  ^+ … + qi ^δx k  ^+ l i  ^{= v, (6.3)}

^где vi^= y i  уравн. ^− y i  измер  ^{− поправка к измеренному значению v, получаемая в}

результате уравнивания параметрическим способом.

Равенства (6.3) – система параметрических уравнений поправок.

В матричной форме

A ∙ δX + L = V, (6.4)

где матрица коэффициентов

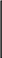46

^a1   ^b1   ^  q1

^{df1 / dX 1    df1 / dX} 2



^df1 / dX k

A 

^a  2  ^b2  ^  q2

             



^df 2 ^/ dX 1















^an  ^bn



^qn

^df n ^/ dX 1





^dfi ^/ dX k

векторы

^δX = [δx 1 ^δx 2  ^… δx k ^];

^L  = [ l1 ^l 2 ^…  l n  ^];

^V = [ v 1 ^v 2   ^…  v n ^].

В соответствии с принципом метода наименьших квадратов систему

уравнений (6.4) решают, обеспечивая условие

F = V ^T ∙P ∙V = min,

(6.5)

где

 − диагональная матрица весов измеренных

P = diag  P =

^p1











^p2











^pn 

^{значений y} i ^.

Для отыскания   min   функции   F   следует найти ее частные произ-

водные по неизвестным параметрам и приравнять их к нулю. В результате

получим выражение

[pav] = 0;

[pbv] = 0; (6.6)

...………

[pqv] = 0,

т.е.  А ^T ∙P ∙ V = 0, (6.7)

называемое леммой Гаусса.

Если будет соблюдено условие (6.7), то при этом будет выполнено и

условие  min  (6.5).

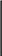
47

^{Подставив в систему (6.6) вместо   v} i  ^{выражение (6.3) образуем сис-}

тему линейных  н о р м а л ь н ы х   у р а в н е н и й.

^[paa] δx 1   ^{+ [pab] δx} 2   ^{+ … + [paq] δx} k  ^{+ [pal] = 0;}

^[pab] δx 1   ^{+ [pbb] δx} 2  ^{+ … + [pbq] δx} k  ^{+ [pbl] = 0; (6.8)}

… … … … …

^[paq] δx 1   ^{+ [pbq] δx} 2  ^{+ … + [pqq] δx} k  ^{+ [pql] = 0,}

^{где [paa] = p} 1 ^a 1   ^a 1  ^+ p 2 ^a  2 ^a 2  ^+ … + p n ^a n  ^a n ^;

… … … … …

^[pal] = p 1 ^a 1 ^l 1  ^+ p 2 ^a 2  ^l 2  ^+ … + p n ^a n  ^l n   ^и т.д.

В матричной форме нормальные уравнения имеют вид

A ^T ∙ P ∙ A ∙  δX + A ^T ∙P ∙ L = 0, (6.9)

^{a1  a2    a}n   ^p1

^a1  ^b1



^q1

^{где AT PA  N} n ^

^b1  b2   ^ bn

              

^p2



^a2 b2   ^ q2

               



q1  q2 qn





 ^paa ^pab  ^  ^paq

pab pbb  ^ pbq

^pn   an  ^bn  ^ q

n

(6.10)









 ^paq ^pbq  ^  ^paa

− матрица коэффициентов нормальных уравнений размером k Û k;

(A^T P L)^T  = [[pal] [pbl] … [pql]]^T (6.11)

– вектор свободных членов размером k Û 1.

Затем  необходимо  решить  систему  нормальных  уравнений.  В  мат-

ричном виде это решение выглядит

δX = − Nn^-1 A^T P L. (6.12)

Полученный  из  решения  вектор  поправок (δx1,  δx2,  …  ,  δxk) к при-

^{ближенным значениям   X} 1^0 , X 02 ^{, … , X 0}k  ^{применяют для определения урав-}

ненных значений, т.е.  Xj = Xj0 + δxj .

48

Может быть найден вектор поправок (6.4) к измеренным элементам,

который служит для вычисления уравненных значений, вектор которых

Yуравн =  Yизме + V.

После этого оценивают точность.