7. 3. Способ полигонов Попова составления нормальных

уравнений по чертежу сети

В  нивелирных  и  полигонометрических  сетях  возникают  условия,

которые называются полигонными.

Например, в свободной нивелирной сети полигоны состоят из замы-

кающихся ходов (рис. 7.1).

Схема несвободной нивелирной сети

Рис. 7.1

На схеме два таких полигона. Они дают простые условные уравне-

ния

^- v2   ^- v3   ^+ v4   ^+ w1 ^= 0;

^- v4   ^- v5   ^+ v7   ^+ w2 ^= 0.

Так как сеть несвободная, т.е. с избытком исходных данных, то есть

еще фиктивные  ходы,  в которых превышения определяются по разности

отметок исходных марок (М10, М21, М60).

Способ  полигонов  Попова  применим  во  всех  случаях,  когда  коэф-

фициенты  условных  уравнений  равны  Ì  1  и  0,  а  сеть  образует  систему

смежных  полигонов.  Составляется  схема  сети,  на  которой  указываются:

61

номера ходов и их направления; номера полигонов и направление подсче-

та невязок в них; невязки и обратные веса ходов.

П р а в и л а  определения коэффициентов нормальных уравнений:

1. Квадратичные коэффициенты равны сумме обратных весов ходов

соответствующих полигонов.

2.  Симметричные  коэффициенты  равны  обратным  весам  смежных

ходов со знаком "-".

3. Свободный член равен невязке полигона, по которому составлено

уравнение.

7.4. Решение нормальных уравнений коррелат

Рассмотрим способ и схему Гаусса. Способ Гаусса предусматрива-

ет последовательное исключение коррелат, начиная с первой, от уравне-

ния  к  уравнению  с  последовательным  преобразованием  коэффициентов

нормальных  уравнений.  Коррелаты  определяют  в  обратном  порядке  от

последней  по  номеру  к  первой.  В  основе  способа  Гаусса  лежит  раз-

деление системы нормальных уравнений (7.15) на две подсистемы:

э к в и в а л е н т н у ю, описывающую последовательное исклю-

чение коррелат с одновременным преобразованием коэффициентов нор-

мальных уравнений:

^[tаа] К1 ^{+ [tаb] К}2 ^{+ [tас] К}3 ^{+ ...  + [tаq] К}r ^+ v1 ^= 0;

^[tbb1] К2 ^{+ [tbс1] K}3 ^{+ ...  + [tbq1] К}r^, + [w2^1] = 0;

^[tсc2] К3 ^{+ ...  + [tcq2] К}r ^+ [w3^2] = 0;

. . . . . . . . . . . .  . .  . . .

^{[tqq(r - 1)] К}r ^+ [wr^{(r - 1)] = 0, (7.16)}

и э л и м и н а ц и о н н у ю, позволяющую получить значения

^{коррелат в обратном ходе решения К}r^, K(r-1)^, ..., К3^, К2^, Кr^:

K1 = − tab

tac ^taq

^taa ^K2 − ^taa ^{K3 −… −} ^taa

^w1

^Kr − ^taa ^;

^K2 ^= −

^tbc1

^tbb1

^K3 ^{− … −}

^{tbq1         w}2^1

^tbb1 ^Kr − ^tbb1 ^;

K3 = − tcq2

^w3^2

^tcc2 ^Kr − ^tcc2 ^;

tbb1  tbb   tab tab  ;

tbc1  tbc   tab tac  ;

tbq1  tbq   tab taq  ;

w21  w2  tab w1 ;

tcc2  tcc  tactac  tbc1tbc1 ;

tcq2  tcq  tactaq  tbc1tbq1 ;

w 2  w   taa w  tbb11 w 1;

62

. .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .   .    .

^wr ^{r  1}

^Kr = − ^tqq^r  1 ^{. (7.17)}

Преобразование,  в  результате  которого  получают  эквивалентную

систему (7.16), называют  т р е у г о л ь н ы м.

Коэффициенты  нормальных  уравнений  преобразовывают  по  сле-

дующим правилам:

^taa 

^taa 

.  .  .  .  .  .  .  .  .  .   .

^taa 

^taa

taa tbb1

.   .   .   .   .   .   .   .   .   .   .    .

taa tbb1

tac tbc

3 3 1 2

.   .   .   .   .   .   .   .   .   .   .    .

tqqr  1  tqq 

^taq2  ^tbq12  ^tcq22  ^tdq32  ...

taa     tbb     tcc2    tdd3

;

wr r 1  wr  taq w1  tbq1w21 tcq2w3 2  tdq3 w4 3.

tcq2  tcq1 tbc1  tbc1tbq1 , где tcq1  tcq  tactaq .

63

^taa ^tbb1 ^tcc2 ^tdd3

В алгоритмах (7.16) цифры 1, 2, 3, ..., (r – 1) в скобках Гауссовых

сумм показывают порядок исключения (преобразования).

Можно показать, что раскрытие промежуточных алгоритмов подчи-

няется тем же правилам, например,

^tbb1 ^tbb1 ^taa

Покажем процесс треугольного преобразования в алгоритмах Гаусса

на примере решения трех нормальных уравнений.

Для  исключения  коррелаты К1  умножим  элементы  первой  строки

матрицы

[tab] [tbb] [tbc]

N = ^{[tab] [tbb] [tbc]}

[tac] [tdc]  [tcc]

tab

tac

последовательно на  коэффициенты

taa 

и

taa

и полученные произ-

ведения вычтем из элементов, стоящих во второй и третьей строках мат-

рицы, т.е. найдем преобразованные элементы

[tbb1] = [tbb] − tab 2

taa 

tac ²

;

[tcc1] = [tcc] −

^taa   ^;

[tbc1] = [tbc]  − tabtac

taa ^.

После первого преобразования получим матрицу

на коэффициент  tbc1

tac2  tbc12

[tcc2] = [tcc1] − tbc1

64

[taa] [tab] [tac]

^{[tbb1] [tbc1]} .

[tbc1] [tcc1]

^{Чтобы исключить коррелату К}2^{, умножим элементы второй строки}

tbb1 ^{. Произведение вычтем из элементов третьей стро-}

ки, т. е. найдем

2

^tbb1   ^{= [tcc]  −} ^taa   ^tbb1  ^.

В результате получим матрицу эквивалентных элементов

[taa]  [tab]

[tac]

^Nэк ⁼

[tbb1]  [tbc1] .

[tcc2]

Соберем  коэффициенты  исключения  в  матрицу  элиминационных

строк

1

^Nэл ⁼

^tab 1

^taa 

.

^{tac tbc 1 }1

^taa  ^tbb 1 

Произведение Nэк ∙ Nэл = N, т. е. приводит к первоначальной матрице

коэффициентов нормальных уравнений.

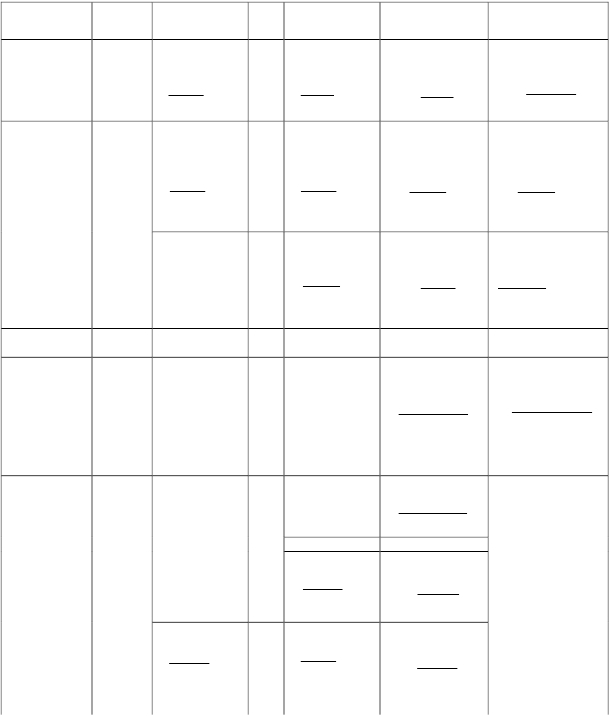
Нормальные уравнения решают по полной схеме Гаусса (табл.1).

При решении  нормальных  уравнений контролируют получение ко-

эффициентов эквивалентных уравнений

65

^{[taa] + [tab] + … + [taq] + w}1 ^= [tas]2^;

^{[tbb1] + … + [tbq1] + [w}2^{1] = [tbs1]}2^;

. . . . . . . .

^{[tqq (r – 1)] + [wr (r – 1)] = [tqs (r – 1)]}2

и   элиминационных строк

= tas 2

^tab ^{tac [taq] w}1

^–1 –  taa  ^–  taa ^{– … –} taa ^–  taa 

taa 

;

–…– tbq1

tbc1

^{–1 –} tbb1

tbb1

^w2^1

^– tbb1

^tbs12

^= –  tbb1

;

–1 – … – tcc2  – w3 2

=– tcs22

tcq2

tcc2

tcc2  ^;

–1 – w (r  1)

.  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .  .   .

r ^{tqs(r  1)}2

tqq(r  1) ^= –  tqq(r  1) ^.

Значение вычисленных по схеме Гаусса коррелат К1, К1, ..., Кr под-

ставляют в уравнение (7.15) и при помощи таблицы находят поправки vi.

Контролем являются равенства

^{[av] = – w}1^{; [bc] = – w}2^{;   [cv] = – w}3^{; …; [qv] = – w}r^,

а также

^{[pv2] = – [kw];   [pv2]  =  – [w}r + 1 ^{r]. (7.18)}

66

Таблица  1

Схема Гаусса

Коэффи-

циент

К1               К2            ...               Кr                      w                          s

[tab]

…

[taq]

w1

[tas]2

1/[taa]

−

tab

taa 

…

−

[taq]

taa

−

^w1

taa 

−

^tas 2

taa 

[tbb]

…

[tbq]

w2

[tbs]2

1/[tbb1]

−

tab

taa 

[tab]

…

−

tab

taa 

[taq]

−

tab

taa ^w1

−

tab

taa  ^[tas]

[tbb1]

…

[tbq1]

[w21]

[tbs1]2

−1

…

– ^tbq1

tbb1

–

^w2^1

tbb1

^tbs12

tbb1

… … … … … … …

[wr(r – 1)]

^[tqs (r – 1)]2

1/[tqq(r –

1)]

[tqq(r – 1)]

–

^wr ^{(r  1)}

tqq(r  1)

–

^{tqs(r  1)}2

tqq(r  1)

Kr = – w (r  1)

r

tqq(r  1)

… …

[wr + 1 r] =

= [tssr + 1 r] =

= [pv²]

tbb1 r

K2 = ^…

–

tbq1

K

–

^w2^1

tbb1

K1 =

−

tab

taa  ^K2

…

−

[taq]

taa ^Kr

−

^w1

taa 

67

^{Выражения в таблице  [w}r + 1 ^r] и [tssr + 1 ^r]2 ^{находят по  формулам}

w1 w 1

[wr + 1 r] = taa +  

+ w  2

w r  1

tcc 2  + … +  tqqr  1 ,

2

2

tbb1

3                                            r

2                                                           ²

[tssr + 1 r] = [w] −

^w1^tas2

taa 



^w2^{1tbs12}

tbb1

 ...  

^wr ^{r  1tqsr  12}

tqqr  1

.        (7.19)

Заключительный  контроль  преобразований  по  схеме  Гаусса  –  это

равенство выражений (7.18) и (7.19).