5. Методические рекомендации
к выполнению контрольных работ
5.1. Контрольная работа 1. Примеры решения
типовых заданий
Задание 1. Даны числа z1, z2, z3. Выполнить следующие действия:
а) в алгебраической, тригонометрической и показательной формах:
если
б)
Значения корня изобразить на комплексной
плоскости.
Решение. а) Выполним последовательно все действия по формулам (1.1–1.4):
Здесь возможно было использование формулы бинома Ньютона. Далее:
Запишем число
в тригонометрической форме. Имеем:
Так как
и
то
Подставляя найденные значения
и
в формулу (1.5), получим
Для числа
имеем x = –1, y = 1,
Так как
и
то
Тогда
Для числа
имеем х = 3,
Так как
и
то
Тогда
Используя формулу (1.9), получим:
Используя формулы (1.7), (1.8), выполним следующие действия:
Выполним действия в показательной форме.
Используя формулу (1.6), представим числа в показательной форме и получим:
Применив формулы (1.10–1.12), получим
б) Запишем число
в тригонометрической форме. Имеем
Так как
и
то
Получим
Значения
вычисляются по формуле (1.13):
где
Подставляя последовательно значения
в последнюю формулу, получим:
Изобразим полученные решения на комплексной плоскости (рис. 5.1).
Рис. 5.1
Задание 2. Найти неизвестную
матрицу Х из уравнения
если
Решение. Домножим уравнение слева
на
Получим
Так как
то
Выполним последовательно действия:
Здесь:
Найдем матрицу
Вычислим:
Так как
то матрица
существует:
Находим алгебраические дополнения:
Следовательно,
Произведение ВС существует, так как число столбцов матрицы В равно числу строк матрицы С. Тогда
Здесь:
Произведение
существует, так как число столбцов
матрицы
равно числу строк матрицы D.
Здесь:
Задание 3. Решить систему уравнений
а) по формулам Крамера;
б) с помощью обратной матрицы;
в) методом Гаусса.
Решение. а) Запишем матрицы А и В:
Вычислим определитель матрицы
:
По правилу Крамера имеем:
б) Так как
то матрица
существует. Найдем алгебраические
дополнения элементов матрицы А:
Тогда
т. е.
Отсюда х1 = 2, х2 = –1, х3 = 3.
в) Выпишем расширенную матрицу системы и с помощью элементарных преобразований ее строк приведем ее к виду, когда под главной диагональю стоят только нули.
Умножим первую строку последовательно на –2 и на –3 и прибавим соответственно ко второй и третьей строкам. Получим:
Умножим вторую строку на –11 и прибавим ее к третьей строке, умноженной на 14:
Тогда соответствующая система уравнений имеет вид
Ее решение находим, начиная с последнего уравнения,
х3 = 3, х2 = –1, х1 = 2.
Приходим к ответу:
.
Задание 4. Даны точки А1(3; 4; 2), А2(–2; 3; –5), А3(4; –3; 6), А4(6; –5; 3). Вычислить:
а)
б)
в)
г) косинус угла между векторами
и
д) площадь треугольника А1А2А3;
е) объем пирамиды с вершинами в точках А1, А2, А3, А4.
Решение. а) Вычислим координаты
векторов
и
Вычислим скалярное
произведение
по формуле (3.2):
б) Вычислим координаты вектора
Векторное произведение
вычислим по формуле (3.6):
в) Вычислим координаты вектора
Смешанное произведение
вычислим по формуле (3.7):
г) Косинус угла между векторами
и
вычислим по формуле (3.4). При этом
воспользуемся результатами вычислений
в пункте а):
д) По свойствам векторного произведения
площадь треугольника А1А2А3
будет равна половине площади
параллелограмма, построенного на
векторах
и
Получим:
е) Объем пирамиды, построенной на векторах
составляет
часть объема параллелепипеда, построенного
на тех же векторах. Тогда по свойствам
смешанного произведения векторов
получим:
Задание 5. Изобразить геометрическое
место точек, заданных уравнением
а) на плоскости;
б) в пространстве.
Решение. а) Данное уравнение есть общее уравнение кривой второго порядка. Методом выделения полного квадрата приведем его к каноническому виду:
Разделив обе части уравнения на 36, получим:
Это уравнение эллипса с центром в точке (1; –3).
График этого эллипса изображен на рис. 5.2.
Рис. 5.2
б) В пространстве заданному уравнению соответствует эллиптический цилиндр, направляющей линией которого является полученный в пункте а) эллипс. Направляющая расположена в плоскости Оху, а образующие – прямые, параллельные оси Оz (рис. 5.3).
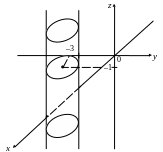
Рис. 5.3
Задание 6. Вычислить пределы функций:
а)
б)
в)
Решение. а) При непосредственной
подстановке в исходное выражение х
= –8 получим неопределенность вида
Умножим числитель и знаменатель дроби
на величину, сопряженную числителю, т.
е. на
и на неполный квадрат разности знаменателя,
т. е. на
Получим:
б) Выделим целую часть в основании степени:
Так как при
исходное выражение представляет собой
неопределенность вида 10, то,
используя второй замечательный предел
(формула (5.2)), имеем:
в) Исходное выражение при
представляет собой неопределенность
вида
Положим х – 2 = у, откуда х =
у + 2.
Так как при
то имеем:
Так как при
имеем
и
то, воспользовавшись таблицей
эквивалентности бесконечно малых,
получим:
при
при
Поэтому
