29. Дайте определения возрастающей и убывающей функций. В чем состоит необходимое и достаточное условия локального экстремума функции.

Теорема (возрастание и убывание на отрезке):1) Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f(x)  0.

2) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f(x) > 0 для a < x < b, то эта функция возрастает на отрезке [a, b].

Анал-но можно сделать вывод о том, что если ф-я f(x) убывает на отрезке [a, b], то f(x)0 на этом отрезке. Если f(x)<0 в пром-ке (a, b), то f(x) убыв на отрезке [a, b].

Конечно, данное утверждение справедливо, если ф-я f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (a, b).

Рассмотрим функцию f(x) на множестве М⊆D(f) . Число f(a) назовем наибольшим значением ф-и f на мн-ве М (абсолютным или глобальным максимумом) и обозначим f(a)=maxx∈Mf(x), если точка a∈М  и f(x)≤f(a)  при любыx x∈M .

Число f(b) назовем наим-им значением ф-и f на мн-ве М (абсолютным или глобальным мин-ом) и обозначим f(b)=minx∈Mf(x), если точка b∈М  и f(x)≥f(b)  при любыx x∈M . Если в качестве множества М рассмотреть некоторую окрестность точки a, то f(a) называют локальным максимумом функции f и обозначают maxU(a)f(x). Если в качестве множества М рассмотреть некоторую окрестность точки b, то f(b) называют локальным минимумом функции f и обозначают minU(b)f(x). Теорема 1: Если функция f во внутренней точке x₀∈D  имеет производную и производная, то f(x₀) не есть локальный экстремум. Теорема (Ферма): Если функция f во внутренней точке x₀∈D  имеет локальный экстремум и дифференцируема в ней, то f′(x₀)=0 (необходимое условие локального экстремума). Теорема 2 (дост усл лок экстремума): Пусть точка x₀- критическая точка ф-и f и пусть ф-я f непрерывна в ней. Если ф-я f дифференцируема в некот выколотой окр-ти U₀(x₀) в точке x₀ и ее производная при переxоде через точку x₀меняет знак, то f(x₀) есть лок экстремум ф-и, причем f(x₀) будет лок max, если производная f ′ при переxоде ч\з точку x₀ меняет свой знак с '+' на '-' и f(x₀) - лок min, если f ′ при переxоде через точку x₀меняет свой знак с '-' на '+'. Теорема 3 (дост усл лок экс): Пусть точка x₀- стац точка ф-и f. Если f дифф-ма в некот окр-ти U(x₀) точке x₀, а в самой точке x₀она дважды диф-ма и f′′(x₀)=0 , то f(x₀) - есть лок экс ф-и f, а именно f(x₀)является лок max, если f′′(x₀)<0и f(x₀) - локальным min, если f′′(x₀)>0.

30. Дайте определения выпуклых вниз и вверх функций одного аргумента. Приведите достаточные условия выпуклости функции. Приведите примеры.

Функция y=f(x) называется выпуклой вверх (вниз) на промежутке х  R, если для любых x1 x2 и x3 этого промежутка выполняется:

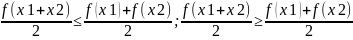
Пример: Функция у = -х² выпукла вверх на промежутке 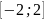, т.к.

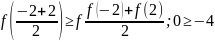
у = -х² , y = -2x, y = -2 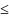0  выпукла вверх

у = х² , y = 2x, y = 2 0  выпукла вниз

Т-ма 1 Ф-я y=f(x) вып вверх (вниз) на числ пром-ке X, если f(x) >0 (соотв-но <0) для всех х  X.