
terve_teoria
.pdf
1. |
Доказать теорему о вероятности суммы совместных событий: |
|
|
|
|
|
|
|
|
|
|
P( A B) P( A) P(B) P( AB) |
|||||||||
|
|
|
|
|
|
|
|
|
||
2. |
Доказать, что если события A и B независимы, то независимы и события |
A и B , A и B , A и B . |
||||||||
3. |
Доказать формулу полной вероятности события. |
|
|
|
|
|
|
|
|
|
4. |
Доказать формулу Бейеса. |
|
|
|
|
|
|
|
|
|
5. |
Вывести формулу Бернулли для вероятности k успехов при n испытаниях, |
проводящихся по схеме Бернулли. |
||||||||
6. |
Вывести формулу для наиболее вероятного числа успехов в серии из n испытаний, проводящихся по схеме Бернулли |
|||||||||
7. |
Доказать предельную теорему Пуассона. |
|
|
|
|
|
|
|
|
|
8. |
Используя интегральную формулу Лапласа, вывести формулу для оценки вероятности отклонения относительной частоты наступления |
|||||||||
|
события A в n независимых испытаниях от вероятности p наступления события A в одном опыте. |
|||||||||
9. Для дискретной случайной величины |
X , распределѐнной по биномиальному закону, |
вывести формулы для вычисления математического |
||||||||||||
ожидания и дисперсии. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10.Для дискретной случайной величины |
X , распределѐнной по закону Пуассона, |
вывести формулы для вычисления математического |
||||||||||||
ожидания и дисперсии. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.Доказать, что для независимых дискретных случайных величин выполняется равенство: |
|
E( X Y ) E( X ) E(Y ) . |
||||||||||||
12.Доказать, |
что для дискретных |
случайных |
величин, принимающих |
конечное |
множество значений, |
|
выполняется равенство: |
|||||||
E( X |
Y ) E( X ) E(Y ). |
|
|
|
|
|
|
|
|
|
|
|||
13.Доказать равенства: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D(X ) E(X 2 ) E(X ) 2 , |
D(X Y ) D( X ) D(Y ) 2cov( X ,Y ) . |
|||||||||||||
14.Доказать, что коэффициент корреляции |
|
( X ,Y ) случайных величин |
X и |
Y подчиняется условию: |
|
(X ,Y |
|
1. Что |
||||||
|
|
|
||||||||||||
можно сказать о величинах, для которых |
|
(X ,Y |
|
1? |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||
15.Для дискретной случайной величины |
X , распределѐнной по геометрическому закону, |
вывести формулу для вычисления математического |
||||||||||||
ожидания. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16.Для дискретной случайной величины |
X , распределѐнной по геометрическому закону, |
вывести формулу для вычисления дисперсии. |
||||||||||||
17.Вывести формулы для математического ожидания и дисперсии непрерывной случайной величины, равномерно распределѐнной на отрезке
a,b .
18. Объяснить
f (x)
19.Объяснить
f(x)
20.Доказать,
(с |
доказательством) |
вероятностный |
смысл |
параметра |
a |
в |
формуле |
для |
функции |
плотности |
вероятности |
||||||
|
|
1 |
|
|
x a 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
2 2 |
случайной величины, распределѐнной по нормальному закону. |
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
(с |
доказательством) вероятностный |
смысл |
параметра |
|
в |
формуле |
для |
функции |
плотности |
вероятности |
|||||||
|
|
1 |
|
|
x a 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
2 2 |
случайной величины, распределѐнной по нормальному закону. |
|
|
|
|
||||||||
|
|
2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
что |
для |
нормально |
распределѐнной величины с |
параметрами |
a |
и |
имеет место |
равенство |
|||||||||
|
|
|
x |
|
a |
|
x a |
|
|
|
|
1 |
|
x |
|
t |
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
e |
|
|
|||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
P(x1 X x2 ) |
|
|
|
|
|
|
1 |
|
|
|
|
, где (x) |
|
|
|
|
2 dt – функция Лапласа. |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||||||
21.Доказать, что |
для нормально распределѐнной |
величины |
с |
параметрами a и |
функция |
|
|
распределения имеет вид: |
|||||||||||||||||||||
|
1 |
x a |
|
|
|
|
|
|
1 |
|
|
x |
|
|
t |
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
F (x) |
|
|
|
|
, где |
(x) |
|
|
|
|
|
|
2 dt – функция Лапласа. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
22.Вывести формулу для вычисления математического ожидания непрерывной случайной величины, распределѐнной по показательному закону.
23.Сформулировать и доказать неравенство Чебышѐва.
24.Сформулировать и доказать теорему Чебышѐва для случайных величин с одинаковыми математическими ожиданиями и дисперсиями, ограниченными одним и тем же числом.
25.Сформулировать и доказать теорему Бернулли (закон больших чисел)

№1
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:
. (3.2.1)
Докажем теорему сложения вероятностей для схемы случаев. Пусть возможные исходы опыта сводятся к совокупности случаев
Предположим, что из этих случаев 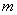 благоприятны событию
благоприятны событию 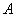 , а
, а  – событию
– событию 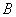 . Тогда
. Тогда
Так как события 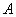 и
и 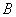 несовместимы, то нет таких случаев, которые благоприятны и
несовместимы, то нет таких случаев, которые благоприятны и  , и
, и 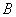 вместе. Следовательно, событию
вместе. Следовательно, событию 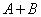 благоприятны
благоприятны  случаев и
случаев и
Подставляя полученные выражения в формулу (3.2.1), получим тождество. Теорема доказана.
Обобщим теорему сложения на случай трех событий. Обозначая событие 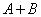 буквой
буквой 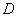 , и присоединяя к сумме еще одно событие
, и присоединяя к сумме еще одно событие 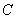 , легко доказать, что
, легко доказать, что
Очевидно, методом полной индукции можно обобщить теорему сложения на произвольное число несовместных событий. Действительно, предположим, что она справедлива для n событий:
и докажем, что она будет справедлива для 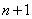 событий:
событий: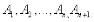
Обозначим: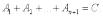
Имеем: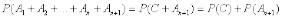 .
.
Но так как для n событий мы считаем теорему уже доказанной, то
,
откуда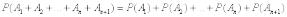 что и требовалось доказать.
что и требовалось доказать.
№2
Пусть вероятность события В не зависит от появления события А.
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:
РA (В) = Р (В). (*)
Подставив (*) в соотношение (***) предыдущего параграфа, получим
Р (A) Р (В) = Р (В) РB (A).
Отсюда
РB (A) = Р (A),
т. е. условная вероятность события A в предположении что наступило событие В, равна его безусловной вероятности. Другими словами, событие A не зависит от события В.
Итак, если событие В не зависит от события A, то событие A не зависит от события В; это означает, что с в о й с т в о н е з а в и с и м о с т и с о б ы т и й
в з а и м н о.
Для независимых событий теорема умножения Р (АВ) = Р (А) РA (В) имеет вид
Р (АВ) = Р (А) Р (В), (**)
т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

№3
Если события H1, H2, …, Hn попарно несовместны и при каждом испытании обязательно наступает хотя бы одно из этих событий, то для любого события А справедливо равенство:
P(A)= PH1(A)P(H1)+ PH2(A)P(H2)+…+ PHn(A)P(Hn) – формула полной вероятности. При этом H1, H2, …, Hn называют гипотезами.
Доказательство: Событие А распадается на варианты: AH1, AH2, …, AHn. (А
наступает вместе с H1 и т.д.) Иначе говоря, имеем А= AH1+ AH2+…+ AHn. Так как H1, H2, …, Hn попарно несовместны, то несовместны и события AH1, AH2, …, AHn. Применяя правило сложения, находим: P(А)= P(AH1)+ P(AH2)+…+ P(AHn). Заменив каждое слагаемое P(AHi) правой части произведением PHi(A)P(Hi), получаем требуемое равенство.
Пример:
Допустим, у нас есть два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго – 0,9. Найдем вероятность того, что взятая наудачу деталь – стандартная.
Р(А) = 0,5*0,8 + 0,5*0,9 = 0,85.
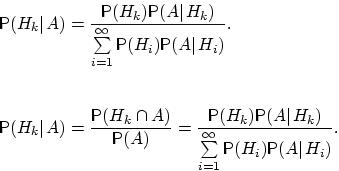
№4
(формула Байеса(1)). Пусть 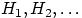 — полная группа событий, и
— полная группа событий, и 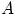 — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что
— некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что
имело место событие 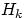 , если в результате эксперимента наблюдалось событие
, если в результате эксперимента наблюдалось событие 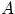 , может быть вычислена по формуле:
, может быть вычислена по формуле:
Д о к а з а т е л ь с т в о . По определению условной вероятности,

№5
Схема Бернулли: производится n независимых испытаний, в каждом из которых с одной и той же вероятностью p наступает некоторое событие А (называемое обычно «успехом») и, следовательно, с вероятностью q=1-p наступает событие A , противоположное А.
Пусть k – любое из чисел 0,1,2,…,n. Обозначим Pn (k ) вероятность того, что в n испытаниях Бернулли успехов наступит k раз.
Справедлива формула Бернулли:
pn (k ) Cnk p k q n k .
Пример: Монета бросается 10 раз. Какова вероятность того, что герб выпадает при этом ровно 3 раза?
Решение: В данном случае успехом считается выпадение герба, вероятность p этого события в каждом опыте равна ½ , так что q=1- p=1|2. Отсюда
P (3) C 3 |
( |
1 |
)3 |
( |
1 |
)7 |
|
10 9 8 |
|
1 |
|
|
15 |
|
|
|
|
1 2 3 |
210 |
128 . |
|||||||||||
10 |
10 |
|
2 |
|
|
2 |
|
|
|
|
|||||
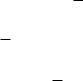
№6
Исследуем случай, когда производится n одинаковых и независимых опытов, каждый из которых имеет только 2 исхода {A; A }. Т.е. некоторый опыт повторяется n раз, причем в каждом опыте некоторое событие А может появиться с вероятностью P(A)=q или не появиться с вероятностью P( A )=q-1=p .
Пространство элементарных событий каждой серии испытаний содержит 2n точек или последовательностей из символов А и A . Такое вероятностное пространство и носит название схема Бернулли. Задача же заключается в том, чтобы для данного k найти вероятность того, что при n-кратном повторении опыта событие А наступит k раз.
Для большей наглядности условимся каждое наступление события А рассматривать как успех, ненаступление А – как неуспех. Наша цель – найти вероятность того, что из n опытов ровно k окажутся успешными; обозначим это событие временно через B.
Событие В представляется в виде суммы ряда событий – вариантов события В. Чтобы фиксировать определенный вариант, нужно указать номера тех опытов, которые оканчиваются успехом. Например, один из возможных вариантов есть
|
|
|
|
|
|
|
Число всех вариантов равно, очевидно, Cnk , а вероятность |
|
( A, A,...,A, A, A,...,A,) . |
||||||||
|
|
|||||||
k |
n k |
|
||||||
каждого варианта |
|
ввиду |
независимости опытов равна p k q n k . Отсюда вероятность |
|||||
события В равна C k p k q n k . Чтобы подчеркнуть зависимость полученного выражения от n |
|||
|
n |
|
|
и k, обозначим его |
P (k ) . Итак, |
P (k ) C k p k q n k . |
|
|
n |
n |
n |
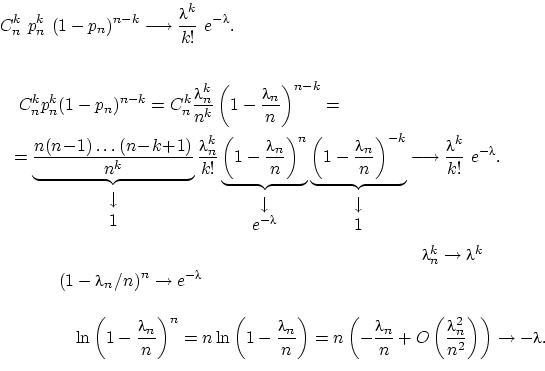
№7
Пусть 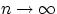 и
и 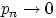 так, что
так, что 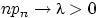 . Тогда для любого
. Тогда для любого 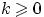 вероятность получить
вероятность получить 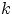 успехов в
успехов в 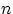 испытаниях схемы Бернулли с вероятностью успеха
испытаниях схемы Бернулли с вероятностью успеха 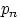 стремится к величине
стремится к величине 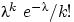 :
:
Д о к а з а т е л ь с т в о . Положим 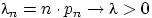 . Тогда
. Тогда 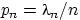 и
и
(8)
В |
соотношении (8) мы |
воспользовались |
тем, |
что |
и |
замечательным |
пределом |
. Докажем последнее свойство: |
|
|
|
||

№8
В условиях схемы Бернулли с заданными значениями n и p для данного >0 оценим
вероятность события |
k |
p |
, где k – число успехов в n опытах. Это неравенство |
|
n |
||||
|
|
|
эквивалентно |k-np| n, т.е. - n k-np n или np- n k np+ n. Таким образом, речь идѐт о получении оценки для вероятности события k1 k k2, где k1 = np- n, k2 = np+ n.
Применяя |
интегральную приближѐнную формулу Лапласа, получим: P( |
k |
p |
) |
||||||||||||||||||||||||
n |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( |
k2 |
np |
) ( |
k1 |
np |
) ( |
|
n |
|
) ( |
n |
|
) . С учѐтом |
нечѐтности функции Лапласа |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
npq |
|
|
npq |
npq |
|
npq |
|
|
|
|
|
|
||||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
получаем приближѐнное равенство P( |
|
p |
) 2Ф ( |
|
n |
) . |
|
|
|
|||||||||||||||||||
n |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pq |
|
|
|
||||||
Примечание: т.к. по условию n=1, то подставляем вместо n единицу и получаем окончательный ответ.
№9
Пусть производится n независимых испытаний, в каждом из которых может появиться событие А с вероятностью р, так что вероятность противоположного события Ā равна q=1-p. Рассмотрим сл. величину Х – число появления события А в n опытах. Представим Х в виде суммы индикаторов события А для каждого испытания: Х=Х1+Х2+…+Хn. Теперь докажем, что М(Хi)=р, D(Хi)=np. Для этого рассмотрим закон распределения сл. величины, который имеет вид:
Очевидно, что М(Х)=р, случайная величина Х2 имеет тот же закон распределения, поэтому D(Х)=М(Х2)-М2(Х)=р-р2=р(1-р)=рq. Таким образом, М(Хi)=р, D(Хi)=pq. По теореме сложения математических ожиданий М(Х)=М(Х1)+..+М(Хn)=nр. Поскольку
случайные величины Хi независимы, то дисперсии тоже складываются:
D(Х)=D(Х1)+…+D(Хn)=npq=np(1-р).
