Файл принадлежит факультету Менеджмента и Социологии, 1 курсу 2009 г. набора. ©

1. Дайте опр-я ф-и, а также сложной и обратной ф-й одной действительной переменной. Найдите обл опр и обл значений функции .

Пусть х, у  R. Если каждому числу х  Х соответствует некоторому правилу единственное число у  У, то говорят, что на мн-ве Х задана ф-я f: у = f (x); X Y.

Если задана функция y=f(x), но при этом x=g(t), то производя замену получим y=f(g(t))- сложная функция(y=sinx,x=t² ,тогда y=sin t²)

Для функции у=f(x) функция x=g(y) называется обратной, если

1)Область значений функции f совпадает с областью определения функции g

2)y=f(g(x))( y = ex, x= ln y) ,

D(y): х€[2пk; п+2пk] k€Z

E(x^2-8x+13)=[-3;∞]

вершина: x=4, y=-3, ветви вверх

2. Сформулируйте св-ва четности, нечетности, периодичности, монотонности, ограниченности ф-и. Определить явл-ся ли след ф-я четной или неч.

Ф-ю f(x), определенную на симметричном относительно 0 промежутке, наз-ют четной, если f (-x) = f (x) для всех х  D(f). Гр чёт ф-и симметричен относительно оси ординат Oy Пример у = х². Ф-ю f(x), определенную на симметричном отн-но 0 промежутке, на-ют неч, если f (-x) = - f (x) для всех х  D(f). График нечётной функции симметричен относительно начала координат. Пример у = х³.

Ф-ю f(x) наз-ют периодической, если сущ-ет Т>0, такое, что для всех x€D, вып-ся x+T€D и f(x+T)=f(x), где T – период. Наим T наз-ся основным периодом ф-и.

Пример: y = sinx T=2п; y=ctgx T=п

Функция y=f(x) называется ограниченной сверху, если f(x) ≤m, снизу f(x) ≥m.

Если |f(x)| ≤m, m>0, то ф-ция ограниченная.

Если |f(x)| ≥m, m≥0, то ф-ция неограниченная.

Пример: y=x²-ограничена снизу 0; y=-x²-ограничена сверху 0; y=x³-неограниченная; y=sinx – ограниченная [-1;1]

Монотонная ф-я. Если ф-я возр или убыв на нек-ом промежутке, то она наз-ся монотонной на этом промежутке. Ф-я f (x) наз-ся возр-ей на пром-ке D, если для люб чисел x1 и x2 из пром-ка D таких, что x1 < x2, вып-ся нер-во f (x1) < f (x2). Ф-я f (x) наз-ся убыв на пром-ке D, если для люб чисел x1 и x2 из пром-ка D таких, что x1 < x2, вып-ся нер-во f (x1) > f (x2). (Критерий мон-ти ф-и, имеющей производную на интервале) Пусть ф-я непрерывна на (a,b), и имеет в каж точке производную f'(x). Тогда f возр на (a,b) т и т т, к

f убывает на (a,b) тогда и только тогда, когда

Пример: y=x² при х (-∞;0] убывает и при х [0;∞) возрастает.

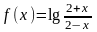– функция нечетная, т.к.

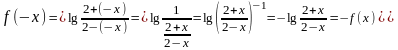
3. Дайте определения числовой посл-ти и предела числовой посл-ти. Сфор-те теорему о единственности предела числовой посл-ти.

Числовой последовательностью называется функция f: N→R, где N=D(f). (N, R с толстой ножкой). Принято обозначение: a₁=f(1), a₂=f(2),…, a_n=f(n),… или {a_n}: a₁, a₂,…, a_n, где a_n =f(n) – общий член посл-ти.

Число а наз-ся пределом числовой посл-ти {an}, если для любого сколь угодно мал ε>0 найдется такое N>0, что для всех членов посл-ти an с номерами n>N вып-ся |a_n-a|<ε. Пример: Известно, что дробь 1/3 представлена в виде беск период дроби 0,333…Образует числовую посл-ть а1=0,3; a2=0,33; a3=0,333…. А потому, если задать к-л беск-но малое Ɛ>0 мы можем найти такой номер N, что |а_n-1/3|< Ɛ при n>N. Н-р, Ɛ=0,001, тогда N=2, т.к. 1/3-а3=1/30000<1/1000

Lim an=1/3 при n стрем.к бесконечности.

Теорема: если a_n имеет предел, то он единственный.

Доказательство. От противного. Пусть {a_n} имеет 2 предела a и b (a≠b). Выберем ε>0 для предела а и σ>0 для предела b, такие, что ε и σ – окрестности точек а и b не пересекаются. Согласно определению найдутся номера N для ε и M для σ, такие что a_N+1, a_N+2,… лежат в ε-окрестности числа а; a_M+1, a_M+2,… лежат в σ-окрестности числа b. Выберем число К=max{M,N}, тогда a_K+1, a_K+2,… лежат одновременно в непересек-ся окр-ях чисел а и b, что невозможно.

4. Дайте опр сходящейся числовой посл-ти и сфор-те основные свойства сходящихся числовых посл-ей. Посл-ть {x_n} наз-ся сходящейся к а, если для любого вещественного числа ε>0 (сколь угодно малого), сущ-ет номер N(ε), начиная с кот для всех членов посл-ти справедливо: |x_n –a|<ε. Это озн-ет, что предел посл-ти {x_n} равен а. Этот факт записывается так: .

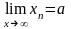Осн-ые св-ва: 1) Сходящаяся посл-ть имеет только один предел. 2) Сходящаяся посл-ть является ограниченной. 3) если члены сходящейся посл-ти удовлетворяют нер-ву xn>=b,то и limxn>=b

4)Пусть имеются 3 посл-ти an,bn,cn,из кот-ых an и cn имеют один и тот же предел а. если an<=bn<=cn при всех n=1,2 то посл-ть bn имеет тот же предел a. 5) lim _n→∞ (a_n±b_n)=a±b

6) lim _n→∞ (a_n*b_n) = lim _n→∞ an * lim _n→∞ b_n = a*b

7) lim _n→∞ (a_n/b_n) = lim _n→∞ an / lim _n→∞ b_n = a/b (bn≠0, b≠0)

Примеры: 1) lim _n→∞ ((1/n)*e^1/n)= lim _n→∞ (1/n) * lim _n→∞ (e^1/n)=0*1=0

2) lim _n→∞ 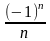равен нуля, т.к. по теореме о 2 милиционерах, он заключен между пределами (-1)/n и 1/n (крайние пределы равны нулю, значит и данный предел тоже равен нулю).

3) lim _n→∞ ((1/n)+e^1/n)= lim _n→∞ (1/n) + lim _n→∞ (e^1/n)=0+1=1

4) lim _n→∞ (2+1/n)/(e^1/n)= lim _n→∞ (2+1/n)/ lim _n→∞ (e^1/n)=2/1=2

5. Дайте определения бесконечно малых и бесконечно больших последовательностей и перечислите их основные свойства. Докажите, что следующая последовательность 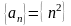бесконечно большая, а последовательность - бесконечно малая.

Функция а(х) называется бесконечно малой величиной при х →Х₀, или при х →∞, если ее предел равен нулю: lim_{х →Х0}а(х) =0.

Св-ва: 1. Алг-ая сумма конечного числа беск малых величин есть вел-на беск малая.

2. Произведение беск малой величины на ограниченную ф-ю есть величина беск малая.

3. Частное от деления бесконечно малой величины на функцию предел которой отличен от нуля, есть величина бесконечно малая.

Ф-я f(х) наз-ся беско большой вел-ой при х →Х0, если для люб даже сколь угодно большого пол-го числа М>0 найдется такое полож число δ > 0(зависящее от М, δ = δ(М)), что для всех х, не равных х₀ и удовл-щих условию |х – х₀|<δ, будет верно нер-во |f{x)| > М.

Свойства: 1. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.

2. Сумма беск бол величины и огран ф-и есть величина беск-о большая.

3. Частное от деления беск большой величины на ф-ю, имеющую предел, есть величина беск большая.

Док.:

А>0

a_n>0 →n²>A → n> квадратный корень из А

Пример: А=50, N=E(квадратный корень из 50)=7; а₈=64>50; a₇=49<50

Ɛ>0 |n/(n²+1)|<Ɛ n²Ɛ-n+Ɛ>0 n²Ɛ-n+Ɛ=0 n(1,2)=(1±квадратный корень из (1-4Ɛ²))/2Ɛ

n>(1+квадратный корень из (1-4Ɛ²))/2Ɛ

N=E[(1+квадратный корень из (1-4Ɛ²))/2Ɛ]

Ɛ=0,1 N=E[9,89]=9 n=9 9/82≈0,1097 n=10 10/101≈0,0990