Teoria_TViMS

1. Что называется случайным событием, связанным с опытом? Как определяется событие, противоположное данному? Приведите примеры.

Случайным событием А, связанным с опытом, называется любое подмножество в пространстве элементарных событий (где каждому эксперименту поставлено в соответствие множество , элементы которого i

отражают описание результатов эксперимента) A . Оно состоит из всех элементарных исходов i ,

которые благоприятствуют появлению события А. Противоположное событие для события А обозначается A . В событие A входят только те элементарных события, которые не благоприятны для А.

Пример. Если А есть выпадание четного числа очков при бросании игральной кости, то A - это выпадание

нечетного числа очков; если А – это попадание при выстреле, то A – это промах. Таблица, характеризующая событие А.

АA

2.Что называется суммой и произведением событий А и В? Имеют ли смысл сумма и произведение

событий, относящихся к разным опытам? Перечислите все случай наступления события AB C

Суммой (А+В) двух событий Аи В называется событие, состоящее в появлении события А или события В, или обоих сразу(события в одном опыте).

Произведением двух событий А и В называется событие АВ, состоящее в совместном появлении (совмещении) этих событий.

Нет, не имеет, тк сумма/произведение связаны с разными опытами, т.е. разными множествами . У них различны область и элементарные исходы.

Таблица, характеризующая событие АВ.

3. Что называется пространством элементарных событий? Что называется случайным событием? Какие исходы называются благоприятными для события А? Что называется вероятностью события А? Привидите примеры.Можно ли в опыте с бросанием игральной кости считать элементарными следующие события: А – выпадение числа очков, меньших 2; В – выпадение более 2 очков?

Пространством элементарных событий называется множество , состоящее из исходов или элементарных событий 1,........, n ,... Случайным событием называется любое подмножество пространства элементарных

событий А , А= 1,........, n ,….

И исходы 1,........, n ,... А – благоприятны для события А. Событие А наступило, если в опыте наблюдался один из благоприятных исходов. Вероятностью случайного события А называется отношение числа благоприятных

исходов k к общему числу исходов n: P(A) = kn (в классическом определении вероятности).

Пример. В опыте с подбрасыванием монеты пространство элементарных событий состоит из двух исходов =G,C , вероятность выпадания герба А= G равна P(A)=0.5

В опыте с подбрасыванием игральной кости пространство элементарных событий состоит из 6 исходов =1,2,3,4,5,6 , А-выпадание четного числа, больше 3, т.е. А= 4,6 , значит Р(А)=2/6=1/3.

1

У нас дано, что А – выпаданее меньше 2, а В – выпадание более 2. Т.о. А = 1 , В= 3,4,5,6 . А- это

элементарное событие, тк состоит из 1 элементарного события; В – не будет элементарным событием, тк состоит из др. элементарных событий.

4. Какие события называются достоверными и невозможными и каковы их ве-

роятности? Пусть A, B и C – случайные события. Перечислите все случаи наступления события AB C .

Событие А, которое произойдет при любом испытании, называется достоверным (А = ). Например, в опыте с подбрасыванием игральной кости событие А, задаваемое условием “число выпавших

очков положительное”, будет достоверным. Вероятность достоверного события равна 1.

Событие А, которое не может произойти при испытании, называется невозможным (А=пуст.множ.). Например, событие А, задаваемое условием “при подбрасывании игральной кости выпало 7 очков”, является невозможным. Вероятность невозможного события равна 0.

Таблица, характеризующая событие А B +С

5.В каком случае событие В называют следствием события А? Какие события называются равными?

Объясните, почему A AB AB .

Событие А влечет за собой событие В или событие В является следствием события А (А В), если каждый исход, благоприятный для А, является благоприятным и для В. События А и В равны (А=В) в случае, когда они являются следствиями друг друга.

I) А АВ+А B

Если А наступило(А=1), то: 1) если В при этом наступило, то наступило АВ АВ+А B наступило; 2) если В не наступило, то B =1 А B =1 АВ+А B наступило.

II) АВ+А B А

Если АВ+А B наступило, то либо АВ наступило (т.е А наступило АВ+А B А) либо наступило А B (А наступило АВ+А B А).

A1 A2 .... An = A1 * A2 *…..* An . Наступление события А 1 +….А n означает, что наступает по меньшей мере одно из событий А 1 ,….,А n . Наступление противоположного события A1 A2 .... An означает, что не наступает

2

ни одно из событий А 1 ,….,А n или, по-другому, что наступают одновременно все события A1 ,…., An , но это в точности означает наступление события A1 * A2 *…..* An . Ч.т.д.

А 1 А 2 A3 + А 1 A2 А 3 + A1 А 2 А 3 : означает наступление ровно двух событий из трех.

8. Докажите, что A1 * A2 *....* An = A1 + A2 +…..+ An . Что означает событие А 1 А 2 + А 1 А 3 + А 2 А 3 ?

9. Сформулируйте статистическое определение вероятности. Почему вероятность удовлетворяет условию 0 P 1? Возможны случаи Р=0 и Р=1? Ответ обоснуйте.

Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0<m<n, значит, 0<m/n<1, следовательно, 0<P(A)<1. Вероятность любого события удовлетворяет двойному неравенству

0≤Р(А)≤1.

В качестве статистической вероятности события понимают относительную частоту или число, близкое к ней. Свойства вероятностей вытекают из классического определения и сохраняются для статистического.

А – случ.событие

N – кол-во опытов, N A -благ.

А- выпала игральная кость, числа которой > 7, P(A)=0 В- выпала игральная кость, числа которой < 7, P(A)=1

10 Сформулируйте и докажите теорему сложения вер-тей для любых событий A и B. Что такое правило сложения вер-тей для несовместных соб. A и B?

Теорема слож. вер-тей. Для любых соб. A и B выполняется формула P(A+B)=P(A)+P(B)-P(AB)Док-во: Обозначим

A + B – A B можно переписать след. образом nA+B=nA+nB-nAB(*).

Разделив почленно формулу (*) на n, получим формулу P(A+B)=P(A)+P(B)-P(AB)

Правило сложения вер-тей. Если соб. A и B несовместны, то P(A+B)=P(A)+P(B).Док-во:Т.е. соб. A и B несовместны,

то P(AB)=0, поэтому из формулы P(A+B)=P(A)+P(B)-P(AB), получим P(A+B)=P(A)+P(B).

11 Какие соб.A1,A2,…An называются попарно несовместными? Сформулируйте правило сложения вер-тей для попарно несовместных соб. A1, A2, …An. Приведите пример попарно несовместных событий A,B, и C,

таких что P(A+B+C)<1?

A1,A2,…An – попарно несовместны, если они никогда не выполняются одновременно. Исходя из следствия, можно сказать, что вер-ть появления одного из нескольких попарно несовместных соб., безразлично какого, равно сумме вер-тей этих соб. P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An).Док-во: Рассмотрим 3 соб.A,B,C. Т.к. рассматриваемые события попарно несовместны, то появление одного из трех событий, A,B,C, равносильно наступлению одного из двух соб,A+B и C, поэтому в силу указанной теоремы

P(A+B+C)=P ( A B) C =P(A+B)+P(C) =P(A)+P(B)+P(C).

Пример: Существуют 5 карточек с написанными цифрами: 1,2,3,4,5.  w1 1; w2 2; w3 3; w4 4; w5 5

5. Соб.А – вытащили карточку с числами, делящимися на 2, В – делящ. на 3, С – делящ. на 5. События А,В,С

попарно независимы. АВ= , АС= , ВС= .  P(A+B+C)=P(A)+P(B)+P(C).

12 Объясните, почему Р(А+В)≤Р(А)+Р(В) для событий A и B. Чему равна сумма P(A)+P( A ) вероятностей

противоположных событий? Ответ обоснуйте.

А и В – как сов., так и несов. события.

Р(А+В)=Р(А)+Р(В) - Р(АВ)

Когда мы считаем P(А+В), то при сложении Р(А) и Р(В) мы дважды учитываем пересечение, то есть его надо вычесть:

Р(А)+Р(В)=Р(АВ)+Р(А В)+Р(А+В)- Р(А В) Р(А)+Р(В)=Р(АВ)+Р(А+В) Р(А+В)=Р(А)+Р(В)-Р(АВ)

Р(А+В)≤Р(А)+Р(В)

Исходя из следствий (теорема сложения вероятностей) можно сказать, что сумма вероятностей противоположных

событий равна единице. P(A)+P( A )=1. Т.к. события A и A несовместны, поэтому можно применить формулу P(A+B)=P(A)+P(B). При этом следует использовать то, что событие A+ A - достоверное, поэтому его вер-ть =1.Также используют такую формулу, выражающую вер-ть события A через вер-ть противоположного события A .

P(A)=1-P( A )

13 Верно ли, что если событие A является следствием события B,то P(A) ≤ P(B)? Ответ обоснуйте.

Да, верно, т.к. согласно следствию: если соб B явл. следствием соб. A, то P(A) ≤ P(B). Т.к. A B, то B=A+(B/A)- сумма несовместных событий. Применяя правило сложения вер-тей, имеем P(B)=P(A)+P(B/A), откуда следует неравенство P(A) ≤ P(B)

14. Дайте определение условной вероятности P( A B) и приведите его статистическую интерпретацию.

Укажите примеры, когда: 1) РB(А)>Р(А); 2) РB(А)=Р(А);

Пусть А и В случайные события по отношению к какому либо опыту причем P(B) неравно 0. число РB(А)=Р(АВ)/Р(В) называют вероятностью события А при условии что событие В уже наступило или просто условной вероятностью А. Наличие условной вероятности (РB(А)≠Р(А)) между событиями определяет их взаимосвязь.

Статистическая интерпретация: Рассмотрим некий эксперимент и 2 соб. А и В. Повторим опыт к раз. Пусть Kn ( A B) - число опытов, в которых произойдет событие А при условии что В тоже произойдет.

1)РB(А)>Р(А) бросаем кость, В- выпало четное, А-выпала двойка. Р(А)=1/6 РB(А)=1/3

2)РB(А)=Р(А). Означает независимость событий А и В. Из колоды игральных карт наугад выбирают 1 карту. А - вынутая карта является тузом, В – в том, что карта красной масти( бубновая и или червовая. Р(А) = 4/36 = 1/9,

РB(А)= Р(А*В)/Р(В)=(1/9*1/2)/1/2 =1/9. Р(А)=1/9 РB(А)=1/9

15. Какие события называются независимыми? Докажите, что если события A и B независимы, то независимы события A и B’

Если выполняется равенство РB(А)=Р(А) то события А и В независимы. Для двух независимых событий А и В имеем Р(АВ)=Р(А)*Р(В)- правило умножения вероятностей для двух событий.

А=АВ+АВ’ Р(А)= Р(АВ)+Р(АВ’), или Р(А)=Р(АВ’)+Р(А)Р(В). Отсюда Р(АВ’)=Р(А) 1-Р(В) , или Р(АВ’)=Р(А)Р(В’)

16. Что такое правило умножения вероятностей: а) для независимых событий A и В? Для любых А и В? Запишите правило умножения вероятностей для

трех (зависимых) событий A,B и C. Приведите примеры применения соответствующих формул.

Для двух независимых событий А и В имеем Р(АВ)=Р(А)*Р(В)- правило умножения вероятностей для двух событий( тк для независ событий РB(А)=Р(А)). Вероятность произведения равна произведению вероятностей. Для двух

любых событий А и В выполняется равенство Р(АВ)=РB(А)Р(В). Для трех любых событий: Р(АВС)=Р(А)РА(В)РАВ(С). Пример: 1)колода карт А- вытянем туза, В – вытянутая карта черной масти. Р(А)=4/36

Р(В)=18/36 всего в колоде два черных туза Р(АВ)=2/36, Р(АВ)=Р(А)*Р(В)

2) В- выпало четное, А-выпала двойка Р(В)=1/2 РB(А)=1/3, Р(АВ)=РB(А)Р(В) Вероятность выпадения двойки 1/6.

4

17. Как определяется независимость в случае трех событий? Рассмотрите при-

мер: пусть в опыте с бросанием двух монет события A, В, С означают: А – на первой монете выпал герб; B

– на второй монете выпал герб; C – обе монеты

упали на одну сторону. Будут ли независимы все три события? Почему?

События А1, А2….Аn являются независимыми если вероятность любого из них не меняется при наступлении какого угодно числа событий из остальных.

Р(АВ)=Р(А)*Р(В); Р(АС)=Р(А)*Р(С); Р(СВ)=Р(С)*Р(В) в системе Р(АВС)=Р(А)Р(В)Р(С)

Все три события не будут независимы так как при событие С зависит от А и В:

Если А и В произошли то Р(С)=1, если А и В не произошли Р(С)=1, а если А произошло а В нет и наоборот Р(С)=0.Поэтому справедливо Р(АВС)=Р(А)РА(В)РАВ(С)= 1/2*1/2*1=1/4

а не Р(АВС)=Р(А)Р(В)Р(С)

18. Как соотносятся понятия независимые события А и В и несовместные события А и В? Следует ли из

независимости событий А,В,С независимость событий АВ и C ? Почему?

Если события независимы то вероятность их осуществления не меняется при наступлении любого количества из них. Если же события несовместны то наступление одного из них исключает наступление второго. В данном

примере надо найти что АВ и C независимы, то есть P(ABC) P(AB)* P(C) .

АB=AB* =AB(C+ C )=ABC+AB C Из несовместности: P(AB)=P(ABC)+P(AB C )=P(AB)P(C)+P(AB C )

Р(АВ C )=Р(АВ)-Р(АВ)Р(С)=Р(АВ)(1-Р(С))=Р(АВ)*Р( C )

19. События А и В независимы, события А и С также независимы. При этом события В и С несовместны. Следует ли из этого, что события А и В+С независимы? Ответ необходимо обосновать.

В и С несовместны, т.е. Р(ВС)=0, т.к. В*С=

Р(А*(В+С))=Р(А)*Р(В+С)-?

из того, что А и В незав Р(АВ) = Р(А)* Р(В) + из того, что А и С незав Р(АС) = Р(А)* Р(С)

Р(АВ)+ Р(АС)=Р(А)*Р(В)+Р(А)*Р(С)=Р(А)*(Р(В)+Р(С))=Р(А)*Р(В+С)( из несовместности) .ч.т.д.

20.События А и В независимы, события А и С также независимы. При этом события В и С несовместны.

Следует ли из этого, что события А и В+С независимы? Ответ необходимо обосновать.

В и С несовместны, т.е. Р(ВС)=0, т.к. В*С=

Р(А*(В+С))=Р(А)*Р(В+С) - ?

1.из того, что А и В незав  А и В  независимы по теореме.

2.из того, что А и С незав  А и С 

Р(А)=Р(А В +АВ)=Р(А В )+Р(АВ-т.к. несовместимы)=Р(А)*Р( В )+Р(АВ)

Р(АВ)=Р(А)-Р(А) Р( В )=Р(А)*Р(В), ч.т.д

Р(А(В+С)=Р(АВ+АС)=(А и С несовм)=Р(АВ)+Р(АС)=(А и В –независ, А и С-независ)=

Р(А)*Р(В)+Р(А)*(Р(С))=Р(А)*(Р(В)+Р(С))=(В и С-несовм)=Р(А)*(Р(В+С)), ч.т.д.

21.Как определяется независимость событий А1,А2,……,Аn , в случае если n>2? Является ли равенство Р(А1А2А3)=Р(А1)*Р(А2)*Р(А3) достаточным для независимости событий А1,А2,А3? Ответ обоснуйте

События А1,А2,……,Аn называются независимыми в сов-ти, если для любого подмножества номеро/индексов:i1 ,i2 ,......in k≤n, выполняется:

Р(Аi1Ai2…Aik) =Р(Аi1)…Р(Aik)

Для независимости 3-х событий необходимо выполнить след. равенства. Р(АВ)=Р(А)Р(В)

Р(АС)=Р(А)Р(С) Р(ВС)=Р(В)Р(С)

5

Р(АВС)=Р(А)Р(В)Р(С)

22. Имеется две игральные кости: одна-симметричная, вторая-несимметричная. Пусть р-вероятность того, что при одновременном броске данных костей на них выпадет одинаковое число очков. Докажите, р=1/6.

1 (i1 , i2 ),i1 ,i2 1;6

6 * 6 36

А-несимметр. кость А (1,1)(2,2)(3,3)(4,4)(5,5)(6,6)

А 6

Р( А) А 1

6

23. В чем состоит геометрический подход к определению вероятности? Как находится вероятность попадания в заданное множество, если точка случайно выбирается на отрезке AB? в треугольнике ABC?

Геометрический подход заключается на предположении, что попадание каждой точки в геометрическом множестве( ), а в какое-то подмножество А . Вероятность Р(А) пропорциональна мере (длин, площади и т.д.) множества А, т.е. Р(А)= с (А) ), где (А)-мера множества А, а с=const. Т.к. P( )=1, то с = 1/ ( ), так что

Р(А)= ( A) .

( )

1) - АВ, F-отрезок СD, СD АВ. - длина, (CD)=d-c, (BA)=b-a, значит

Р(А)= d c . b a

2) -треугольник АВС, F-фигура . (F)=площадь F, ( )-площадь АВС. Р(F)=площадь F/ площадь

ABC.

24. В чем состоит геометрический подход к определению вероятности? Как находится вероятность попадания в заданное множество, если точка случайно выбирается в круге радиуса r? в кубе со стороной a?

Геометрический подход заключается на предположении, что попадание каждой точки в геометрическом множестве( ), а в какое-то подмножество А .Вероятность Р(А) пропорциональна мере (длин, площади и т.д.) множества А, т.е. Р(А)= с (А), где (А)-мера множества А, а с=const. Т.к. P( )=1, то с = 1/ ( ), так что

Р(А)= ( A) .

( )

1) - круг с радиусом r F – фигура

(F)=площадь F( )=площадь

P(F)=площадь F/площадь круга радиуса r

2) P(F)=объем F/ объем круга

25. Что такое полная группа событий? Приведите пример, когда события АВ, AB и A B не образуют

полной группы событий.

Полная группа событий - это система случайных событий такая, что в результате произведённого случайного эксперимента непременно произойдёт одно из них.

АВ, А*В, А*+*В (чёрточка одна на А и В)-не образуют полной группы событий. А*+*В(чёрточка одна на А и В)=А*В* Полную группу событий составляют: АВ, А*В, АВ*, А*В*

Сл-но АВ, А*В, А*В* - не образуют полной группы.

Пример: студент сдаёт 2 зачёта, соб.А- сдан 1 зачёт, соб.В- сдан 2 зачёт, Р(А)=1/2, Р(В)=2/3 Р(АВ+А*В+А*В*)≠1, т.к. Р(АВ*)≠0, сл-но соб. АВ, А*В, А*+В* (чёрточка одна на А и В)-не образуют полной группы.

6

26. Верно ли, что события AB, AB, AB,AB образуют полную группу для любых событий А и В? Ответ

обоснуйте.

Да, события AB, AB, AB,AB образуют полную группу событий для любого А и В, т.к. они попарно несовместны и при каждом осуществлении опыта обязательно наступит хотя бы одно из них. (проиллюстрировать рисунком)

27 Событие А влечет за собой событие В. Верно ли, что Р(А)+Р(А*В)+Р(В*)=1?

Да, верно. Так как А вслечет за собой В, то если не произошло А, то не произошло и следствие А, то есть Р(А*В)=Р(А*В*)=0. То, что В – следствие А значит, что каждый благоприятный для события А исход является благоприятным для события В, Р(В*) означает, что нет благоприятных исходов события В, а значит нет благоприятных исходов события А, сл-но Р(В*)=Р(А*). Р(А)+Р(А*) образуют Ω, а Р(Ω)=1.

Если в каждом из n независимых испытаний вероятность р появления A const, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абс величине будет сколь угодно

событий в i-м испытании (i=1…n). Каждая из величин может принимать 2 значения: 1 с вер-ю р, 0 с вер q xi- попарно независ., тогда D(xi)=pq. Т.к. p+q=1, то pq 1/4 дисперсии огранич с=1/4

Применим т. Чебышева, получим lim p(|(x1 ... xn ) / n a | ) 1

n

Матем ожидание а каждой из величин xi = р наступл. событ. lim p(|(x1 ... xn ) / n p | ) 1

n

Каждая xi при появлении события в соотв. испытании принимает значение = единице x1+x2+…+xn= m появлен. события в n испытаниях ( x1+x2+…+xn)/n= m/n.

Учитывая это, получим, lim p(| mn p | ) 1

n

28. Сформулируйте и докажите формулу полной вероятности. Приведите пример ее применения.

Рвn (А) события А. Найдем вероятность события А.

Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В1, В2,…,Вn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

Р(А) = Р(В1) Рв1(А) + Р(В2) Рв2(А) +….+ Р(Вn) Рвn(А).

Эта формула называется «формулой полной вероятности». Докажем ее…

По условию, событие А может наступить, если наступит одно из несовместных событий В1,В2,…,Вn. Другими словами, появление события А означает осуществление одного, безразлично какого, из несовместных событий В1А, В2А,…, ВnА. Пользуясь для вычисления события А теоремой сложения, получаем

Остается вычислить каждое из слагаемых. По теореме умножения вероятностей зависимых событий

имеем:

Р(В1А) = Р(В1) Рв1(А); Р(В2) Рв2(А): …. Р(ВnА) = Р(Вn) Р( bn) (А)

Подставляем правые части этих равенств в соотношение (1) и получаем формулу полной вероятности:

7

Р(А) = Р(В1) Рв1(А) + Р(В2)Рв2 (А) + ….+ Р(Вn) Рвn (А)

Приведем пример использования формулы полной вероятности:

Допустим, у нас есть два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго – 0,9. Найдем вероятность того, что взятая наудачу деталь (из наудачу взятого набора) – стандартная.

Пусть А событие «извлеченная деталь стандартна». Деталь может быть извлечена либо из первого набора (событие В1), либо из второго (В2). Вероятность того, что деталь вынута из первого набора, Р(В1) =1/2, вероятность, что деталь вынута из второго набора, Р(В2) = 1/ 2. Условная вероятность того, что из первого набора будет извлечена стандартная деталь, Рв1 (А) =0,8, условная вероятность того, что из второго набора будет извлечена стандартная деталь Рв2(А) =0,9.

Искомая вероятность того, что извлеченная наудачу деталь – стандартная, по формуле полной вероятности

равна

Р(А) = Р(В1) Рв1(А) + Р(В2)Рв2 (А) = 0,5*0,8 + 0,5*0,9 = 0,85.

29. Сформулируйте и докажите формулу Байеса. Приведите пример ее применения.

Пусть событие А может наступить при условии появления одного из несовместных событий В1,В2,…,Вn, образующих полную группу. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности:

Р(А) = Р(В1) Рв1(А) + Р(В2)Рв2 (А) + ….+ Р(Вn) Рвn (А) (1)

Допустим, что произведено испытание, в результате которого появилось событие А. Определим, как изменились, в связи с тем, что событие А уже наступило, вероятности гипотез. Другими словами, будем искать условные вероятности

Ра(В1), Ра(В2),…., Ра(Вn).

Найдем вначале условную вероятность Ра(В1). По теореме умножения имеем

Р(АВ1) = Р(А) Ра(В1) = Р(В1)Рв1(А)

Отсюда

Ра(В1) = Р(В1)Рв1(А)

Р(А)

Заменим здесь Р(А) по формуле (1), получаем

pA(Hi)= рвi(A)p(Вi) .

рВ1(А1)р(В1)+рВ2(А)р(В2)+…+рВn(А)р(Вn)

Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т.е. условная вероятность любой гипотезы Вi (i= 1,2,…,n) может быть вычислена по формуле

Ра(Вi) = Р(Вi) Рвi(А)

Р(В1) Рв1(А) + Р(В2) Рв2(А)+….+Р(Вn) Рвn(А)

Полученные формулы называются формулы Байеса. Они позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.

Пример:

Имеется три одинаковых по виду ящика. В первом ящике n=12 белых шаров, во втором – m=4 белых и n-m=8 черных шаров, в третьем – n=12 черных шаров. Из выбранного наугад ящика вынули белый шар. Найдите вероятность Р того, что шар вынут из второго ящика.

30. В чем состоит схема Бернулли? Запишите формулу Pn (k) для вероятности k успехов в серии n

испытаний по схеме Бернулли и приведите пример ее применения.

Схема Бернулли: производится n независимых испытаний, в каждом из которых с одной и той же вероятностью p наступает некоторое событие А (называемое обычно «успехом») и, следовательно, с вероятностью q=1-p

наступает событие A , противоположное А.

Пусть k – любое из чисел 0,1,2,…,n. Обозначим Pn (k) вероятность того, что в n испытаниях Бернулли успехов

наступит k раз. Справедлива формула Бернулли:

pn (k) Cnk pk qn k .

Пример: Монета бросается 10 раз. Какова вероятность того, что герб выпадает при этом ровно 3 раза?

8

32. Вывыедите формулу для наиболее вероятного числа успехов в серии n испытаний по схеме Бернулли.

Рассмотрим 2 соседних числа Рn(k) и Рn(k+1). Они либо равны, либо 1<2го, либо 2<1го. Рn(k)/ Рn(k+1)<>=1.

Рn(k)=Сnkpkqn-k; Pn(k+1)=Cnk+1pk+1qn-k-1. Cnk+1=Сnk*(n-k)/(k+1). Сл-но (k+1)/(n-k)<>=1. Или (k+1)*q<>=(n-k)*p. Сл-но k<>=n*p-q. Обозначим np-q как a. Сл-но для любого k<a-1 справедливо Pn(k)<Hn(k+1), для k=a-1 (если а – целое

число) Pn(k)=Pn(k+1), при k>a-1, Pn(k)>Pn(k+1). При k<a-1 функция Pn(k) возрастает, при k>a-1, убывает.То есть, если а не являя-ся целым, то ф-я имеет единственный максимум, он достигается при ближайшем к а слева целом значении k, k=[a]=[n*p +p]. Если а =целое, то 2 разных максимума достигаются при k=a-1, k=a.

33. Пусть Pn (k) - вероятность k успехов в серии n независимых испытаний с вероятностью успеха p в каждом испытании. При каком k вероятность Pn (k) достигает максимума? Совпадает ли это число с

n 1

математическим ожиданием количества успехов? Чему равна сумма Pn (k ) ?

k 0

Рассмотрим 2 соседних числа Рn(k) и Рn(k+1). Они либо равны, либо 1<2го, либо 2<1го. Рn(k)/ Рn(k+1)<>=1.

Рn(k)=Сnkpkqn-k; Pn(k+1)=Cnk+1pk+1qn-k-1. Cnk+1=Сnk*(n-k)/(k+1). Сл-но (k+1)/(n-k)<>=1. Или (k+1)*q<>=(n-k)*p. Сл-но k<>=n*p-q. Обозначим np-q как a. Сл-но для любого k<a-1 справедливо Pn(k)<Hn(k+1), для k=a-1 (если а – целое

число) Pn(k)=Pn(k+1), при k>a-1, Pn(k)>Pn(k+1). При k<a-1 функция Pn(k) возрастает, при k>a-1, убывает.То есть, если а не являя-ся целым, то ф-я имеет единственный максимум, он достигается при ближайшем к а слева целом значении k, k=[a]=[n*p +p]. Если а =целое, то 2 разных максимума достигаются при k=a-1, k=a.

n 1

Pn (k ) =1-pn

k 0

34. Может ли наиболее вероятное число успехов в схеме Бернулли отличаться от математического ожидания числа успехов на 2? Ответ обоснуйте.

По схеме Бернулли наиболее вероятное число успехов: k=np+p.

Мат. ожидания: так как схему Бернулли можно представить как биноминальное распределение M(x)=np np+p-np=p Следовательно, в схеме Бернулли наиболее вероятное число успехов может отличаться от мат. ожидания на число р - вероятность успеха и известно, что p+q=1, p=1-q p<1. А значит отличаться на 2 не может.

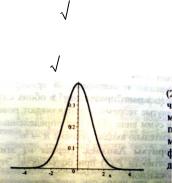
35. Запишите локальную приближенную формулу Лапласа, приведите основные свойства функции Гаусса

ϕ (x) и укажите ее график. При каких условиях данная формула дает хорошее приближение? Какие условия

применимости отличают эту формулу от приближенной формулы Пуассона?

Если число опытов достаточно велико но не бесконечно, а вероятность появления события А в каждом опыте не стремится к 0, применяют локальную и интегральную теоремы Лапласа

Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях в каждом из которых вероятность появления события А равно р причем 1>р>0, то это событие наступает ровно m раз приблизительно равна

Основные свойства ф-и Гаусса: 1)f четная ф-я, 2) max(f)=f(0)=1/√2π; 3) f Гаусса обладает св-м нормированности ∫-∞∞f(x)dx =1. Хорошая точность при n>>100, npq>10/ Пуассон применяется, когда р стремится к 0 или 1

10