Teoria_TViMS

0, x ax

F (x) f (t)dt, a x b,

a

1, x b

74. Перечислите основные свойства функции плотности вероятности. Чем объясняется название «плотность вероятности»?

Св-ва плотности:

1.f(x) 0

2.f (x)dx 1

3.во всех точках, где ф-ция плотности непрерывна вып. равенство

f(x)=F’(x)

Поясним смысл назв. «плотность вероят-ти» x2

P x1 x x2 f (x)dx

Отношение, стоящее под знаком предела, есть своего рода «вер-ть на ед-цу длины» интервала x2 , x1 . Предел

этого отношения рассмотрим как плотность вероятности в самой т. x0 . Во всякой т. x0 , где f(x) непрер., число f(x) совп. с поним-й плотностью вер-ти в т. x0 . Что и требовалось доказать.

75. Показательный закон.

Случайная величина Х, принимающая только неотрицательные значения, распределена по показательному закону, если для некоторого параметра λ›0 функция плотности имеет вид:

f(x)= λe-λx, x≥0

График функции плотности Функцию распределения найдем по формуле

F(x)=∫x0f(t)dt

Подставляя выражение для функции плотности, получим

F(x)=∫x0 λe-λtdt=-e-λt 0 1=1- e-λx, x≥0

21

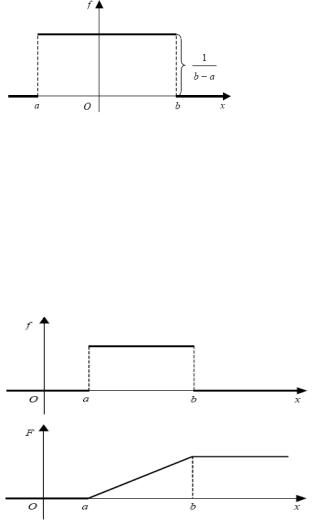
76. Как определяется равномерный закон распределения на отрезке [a, b]? Укажите формулу для функции плотности f(x), найдите соответствующую функцию распределения F(x) и постройте графики функции f(x) F(x).

Скажем, что случайная величина X, сосредоточенная на отрезке [a, b], равномерно распределена на этом отрезке, если ее функция плотности равна константе:

f (x) c(const), a x b

Значение постоянной с определяется из условия:

f (x)dx 1

Графикf(x)

Связь между функцией распределения и плотностью вероятности дается форму-лой

x

F (x) f (t)dt

a

Подставляя сюда функцию f(t), получим:

для x a, F (x) 0

для x b, F (x) 1

77. Возможно ли равномерное распределение на всей числовой оси? Чему равна вероятность Р(c<X<d) для равномерно распределенной на отрезке [a,b] случайной величины Х? Рассмотрите случаи: 1) c>a, d<b и 2) c<a, d<b.

1)Р(c<X<d)= cd f (t)dt

d

2) Р(c<X<d)= a f (t)dt

Непрерывная СВ Х имеет равномерный закон распределения на всей числовой оси, если ее плотность вероятности f(x) постоянна на всей числовой оси, т.е. f(x)=const.

22

78. Как определяется нормальный закон распределения на прямой? Укажите формулу для функции плотности f (x) , найдите соответствующую функцию распределения F(x) и приведите формулу для вычисления вероятности P(α ≤ X ≤ β ) .

Мы говорим, что непрерывная случайная величина Х подчиняется нормальному закону распределения, если она имеет плотность вероятности следующего специального вида:

f x Ae ( x a)2 , где

А, и а – постоянные, причем А>0, >0.

Стандартная запись функции плотности нормального закона распределения.

79. Запишите плотность распределения нормальной случайной величины x, для которой М(x)=m, D(x)=δ2. Как изменится график плотности распределения, если: а) увеличится m, б) увеличится δ?

а) известно, что графики функций f(x) и f(x-a) имеют одинаковую форму: сдвинув график f(x) в положительном направлении оси x на а единиц масштаба при а<0 получим график f(x-a). Отсюда следует, что изменение величины параметра m (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к её сдвигу вдоль оси Ох. При увеличении m график плотности сдвинется вправо.

23

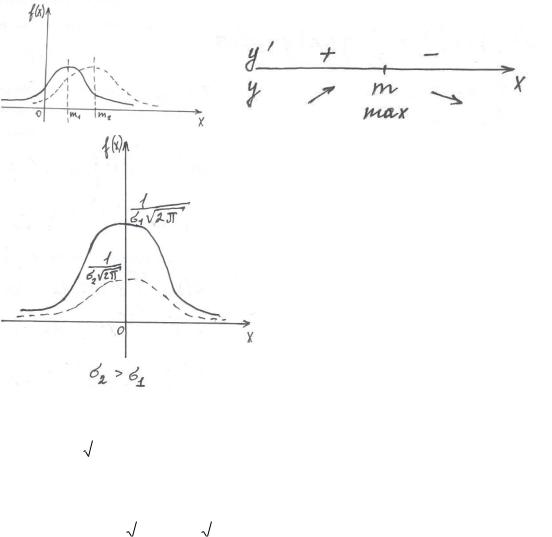
2) Исследуем функцию на экстремум.

f’(x)=0 при x=m

При x=m функция имеет максимум

С возрастанием δ максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси Ох.

80. Как вычисляется математическое ожидание в случае распределения с плотностью f(x)? Может ли для какой-либо абсолютно непрерывной случайной величины не существовать математического ожидания? Ответ обоснуйте.

Математическое ожидание абсолютно непрерывной СВ Х с функцией плотности f(x) определяется равенством: М(Х)= интеграл xf(x)dx от минус беск до плюс беск

указанный справа предел не существует, то мат. ожидание величины х также считается несуществующим.

Если дискретная случайная величина Х принимает счетное множество возможных значений, то M ( X ) xi pi ,

i 1

причем мат. ожидание существует, если ряд в правой части равенства сходится абсолютно. Т.к. ряд может и расходиться, то соотв. случайная величина может и не иметь мат. ожидания. На практике, как правило, множество возможных значений случайной величины распространяется лишь на ограниченный участок оси абсцисс и, значит, мат. ожидание существует.

81. Как вычисляется дисперсия в случае распределения с плотностью f (x)? Докажите, что для случайной

M(X ) существует.

24

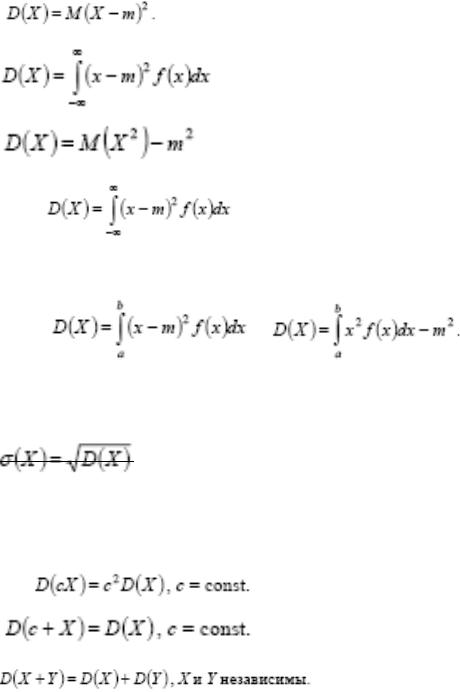
Дисперсия абсолютно непрерывной случайной величины.

Дисперсия абсолютно непрерывной случайной величины X с функцией плотности f(x) и математическим ожиданием m = M(X) определяется таким же равенством, как и для дискретной величины

Из равенства (5.26) следует, что справедлива следующая формула

Поскольку формула (5.29) может быть записана в следующем виде

то формулу (5.30) можно представить таким образом

В случае когда абсолютно непрерывная случайная величина X сосредоточена на промежутке [a, b], формулы

(5.30), (5.32) примут вид

.

Дисперсия непрерывной случайной величины определяет степень рассеивания значений, принимаемых случайной величиной, вокруг ее математического ожидания.

Среднее квадратичное отклонение, или стандартное отклонение, непрерывной случайной величины X определяется так же, как и для дискретной случайной величины:

4°. Свойства математического ожидания и дисперсии.

Для математического ожидания и дисперсии непрерывной случайной величины X сохраняются свойства числовых характеристик дискретной случайной величины. Напомним эти свойства.

4.Постоянный множитель выносится из под знака дисперсии в квадрате.

5.Если к случайной величине прибавить константу, то дисперсия не изменится.

6.Дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин.

Док-во по формуле

82. Выведите формулу для нахождения мат. ожидания и дисперсии случайной величины, равномерно распределенной на отрезке [a; b].

C.В. Х, сосредоточенная на [a;b], равномерно распределена на этом отрезке, если её функция плотности равна константе: f(х)=с (const), a≤х≤b.

Значение постоянной с определяется из условия: ∫∞-∞ f(х)dх=1, которому удовлетворяет любая плотность вероятности. В данном случае это условие принимает вид: с(b-a)=1, откуда следует, что с=1/(b-a).

М(Х)= ∫ba хf(х)dх= ∫ba сdх, т.к. для абсолютно непрерывной С.В. Х с непрерывной плотностью f(х) М(Х)= ∫ba

хf(х)dх.

Т.к. с=1/(b-a), то М(Х)=с*х2/2 |ba = c*(b2-a2)/2=(b+a)/2. Таким образом мы получили, что числу М(Х) соответствует середина [a; b].

Для нахождения дисперсии воспользуемся формулой, где D(Х)= ∫ba х2f(х)dх- m2, где m=M(Х).

D(Х)= 1/(b-a) ∫ba х2dх – ((a+b)/2)2= 1/(b-a)*(b3-a3)/3 - ((a+b)/2)2= (b2+ab+a2)/3 - ((a+b)/2)2= (b-a)2/12.

Таким образом, М(Х)=(b+a)/2, а D(Х)= (b-a)2/12.

25

Нормальное распределение определяется двумя параметрами: m и . Докажем, что вероятностный смысл этих параметров таков: m есть математическое ожидание.

По опр мат ожидания непрерывной с.в.,

x z m, dx dz . Приняв во внимание, что новые пределы интегрирования равны старым, получим

Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны

x m z, dx dz .Приняв во внимание, что новые пределы интегрирования равны старым, получим

распределения равно параметру .

85. Докажите, что для случайной величины, распределенной по показательному закону с параметром ,

математическое ожидание M (x) 1

Найти числовые характеристики случайной величины X, распределенной по пока-зательному закону с плотностью f (x) e x , 0, x 0

Решение. Для нахождения математического ожидания воспользуемся формулой

M(X)= xf (x)dx xe x dx

0 0

Найдем интеграл методом интегрирования по частям, полагая u = x, dv = e–λxd(λx), так что du = dx, v = –e–λx.

26

86 Случайная величина X равномерно распределена на отрезке [a,b]. Можно ли для любых m и δ>0 подобрать параметры a и b так, чтобы M(x)=m, D(x)=δ2? Как по m и δ найти a и b?

Если M(x)=m, а D(x)= δ2 и m, δ>0 – любые, тогда мы всегда можем подобрать параметры a и b, чтобы выполнялось это условие.

87.Что такое правило 3 для нормального распределения? Верно ли, что для любой нормальной случайной величины Х существует отрезок a;b , для которого P( X a,b ) 1? Ответ обоснуйте.

Правило трех сигм – отклонение любой случайной величины от ее математического ожидания будет не более трех средних квадратических отклонений (по абсолютной величине). Правило трех сигм применимо для большинства СВ, встречающихся на практике. P (|X-a|<=3сигма) для нормального закона = 0,9973. Для равномерного закона =1. Для показательного = 0,9827 и т.д.

Для нормально распределенной с.в.Х справедлива формула P(| X a | ) 2Ф( / ). Преобразуем эту формулу, приняв t. В итоге получим

абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.

2. Верно, если границы отрезка не являются конечными. Эта вер-ть равна Ф(b-m/сигма )-Ф(a-m/сигма), а это выр-е

=1, если (-∞;∞)

88. Формулируйте определение начальных 1 , 2 ... _ и _ центральных _ 1 , 2 моментов случайной величины. Докажите, что если Х и У независимые случайные величины, то 3 Х У 3 X 3 (Y )

Начальным моментом порядка k (k принадлежит N), свободная величина Х называется мат.ожиданием k-й степени Х.

Центральным моментом порядка k СВ Х называется мат.ожидание k-й степени отклонения:

X X M X

27

3 X 3 2 X 1 Y 3 1 X 2 Y 3 Y 3 X 3 Y

89. Пусть 1 _ и _ 2 - начальные, а 1, 2 ... - центральные моменты некоторой случайной величины.

Докажите, что: 3 3 3 1 2 2 13 _ и _ 4 4 4 1 3 6 12 2 3 14

Докажем связь начальных и центральных моментов:

1 x M x ; 2 x M x 2

3 X M X M X 3 M X 3 3X 2 M X 3X M X 2 M X 3

M X 3 3M X M X 2 3 M X 3 M X 3

4 X M X M X 4 M X 4 4 X 3 M X 6 X 2 M X 2 4 X M X 3 M X 4

M X 4 4M X 3 M X 6M X 2 M X 2 4 M X 4 M X 4

4 4 3 1 6 2 12 3 14

90. Сформулируйте определение асимметрии As(X ) случайной величины X и укажите ее основные свойства. Что характеризует асимметрия случайной величины?

Определение. Асимметрией распределения называют отношение третьего центрального момента к кубу стандартного отклонения:

As 3

3

Замечание. Асимметрия случайной величины X совпадает с третьим начальным (центральным) моментом соответствующей нормированной случайной величины.

Свойство 1. Асимметрия и эксцесс инвариантны относительно линейной замены случайной ве-личины:

As(aX b) As(X )

Таким образом, асимметрия и эксцесс не меняются при сдвигах и растяжениях и их можно ис-пользовать в

В случае одинаково распределенных НСВ X1, …, Xn асимметрия и эксцесс их суммы стремится к нулю, когда n

3

→ : As( X1 ... X n ) n2 As( X1 ) 0

28

91. Сформулируйте определение эксцесса Ex(X) случайной величины X и укажите его основные свойства. Чему равен эксцесс для нормального распределения?

Эксцессом распределения назыв. величина:

Ex 4 34

для норм. распределения Ex=0 (поскольку для станд. норм. распред. N(0,1) 4 3 )

Св-ва:

1 Ex aX b Ex X

2 Ex x1 ... xn b1 Ex x1 ... bn Ex xn

b 4 xi i 2 x1 ... 2 xn 2

i=1,…,n

x1 ,..., xn им. один дисперсию, то

Ex x1 ... xn n 2 Ex x1 ... Ex xn

В случае одинаково распред. нез. сл. вел x1 ,..., xn

Ex x1 ... xn n 1 Ex x1 0

92 Найдите асимметрию и эксцесс равномерного распределения на отрезке [а,b].

Тк As и Ex не меняются при меняющихся заменах, а любое равномерное распределение на отрезке может быть получено линейной заменой из любого другого равномерного распределения, например, из равномерного распределения на отрезке, то достаточно посчитать As и Ex для этого распределения.

As=μ3/σ3, σ=√D, μ3=M[(x-M(x)3] Ex= μ4/σ4-3

Плотность fx=1/(b-a)=1, μ3= Sb a fx(t)tdt== Sb a tdt=t2/2 в пределах от a до =(b-a)2/2 D== Sb a fx(t)t2dt=(b-a)3/3

σ=√D=√(b-a)3/3 As=μ3/σ3=((b-a)2/2)/( √(b-a)3/3 )

Ex= μ4/σ4-3=((b-a)5 /5)/(( b-a)3/3)2 - 3 μ4= M[(x-M(x)4] fx(t)tdt= Sb a t4dt=(b-a)5 /5

93.Что называется системой случайных величин? Сформулируйте определение функции распределения двумерного случайного вектора (Х,Y) и дайте его геометрическую интерпретацию.

Определение. Упорядоченная пара случайных величин (X, Y), определенных на одном и том же пространстве элементарных событий Ω, называется системой случайных величин, двумерным случайным вектором или двумерной случайной величиной.

Определение. Функцией распределения двумерной случайной величины (X, Y) называется ве-роятность совместного выполнения двух событий X < x и Y < y

FX ,Y (x, y) P(X x,Y y)

Геометрической интерпретацией может служить рис, на котором значением функции распределения может служить вероятность попадания случайной величины (X, Y) в бесконечный квад-рант Q(x, y) с вершиной в точке (x, y), лежащий левее и ниже ее.

29

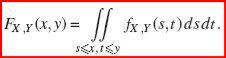
94. Сформулируйте основные свойства функции распределения случайного вектора (Х,У) и приведите примеры двумерной функции распределения.

1.F(x,y) не убывает по икс и по у

2.F(x,y) непрерывна слева по любому аргументу

3.F(-∞;∞) =1, F(-∞;x)=F(-∞;y)=0

4.P(x1<=X<=x2, y1<=Y<=y2)= F(x2,y2)-F(x2,y1)-F(x1y2)+F(x1y1)

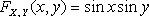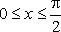Пример , где и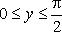

95. Какой случайный вектор называется абсолютно непрерывным? Укажите основные свойства функции плотности распределения двумерного случайного вектора. Как можно найти непрерывную функцию плотности распределения двумерного случайного вектора, если известна его функция распределения? Укажите функцию плотности для равномерного распределения в круге радиуса R.

Случайный вектор называется абсолютно непрерывным, если существует f (x; y) 0 - плотность распределения, такая, что:

P((x; y) G) f (x; y)dxdy по обл-ти G

Свойства f(x;y):

1)f(x;y) – неотрицательная

2)f (x; y) dxdy=1

Если F(х;у) известна => F '' (x, y) f (x; y) - в точках непрерывности f(x,y).

xy

Пример: Случ вектор (Х;У) равномерно распределен в круге радиуса R. Найти функцию плотности.