Teoria_TViMS

f (x; y) fx (x) f y ( y)

Компоненты Х и У - независимые

99. Как можно найти функцию распр Fx,y(x,y) случайного вектора (X,Y) с независимыми компонентами X и Y, если известны их ф-ии распр FX(x) и FY(y)?

Если X и Y – независимые компоненты случ вектора (X,Y) и известна их ф-ия распр FX(x) и FY(y), то его ф-ия распр

Fx,y(x,y)= FX(x)*FY(y). Обоснование.

Пусть A=(X<x), B=(Y<y), тогда P((X A)(Y B))=Fx,y(x,y) и P(X A)*P(Y B)= FX(x)*FY(y), т.к. P((X A)(Y B))=P(X A)*P(Y B) (т.к. X и Y –независимые).

100. Как найти математическое ожидание функции x, y , где Х,У – компоненты случайного вектора (Х,У)?

Как определяются начальные k,l и центральные k,l моменты случайного вектора (Х,У)?

Для математического ожидания функции ф(х, у) от компонент случайного вектора (X, Y) справедлива формула

В одномерном случае основные числовые характеристики случайной величины выражались через начальные и центральные моменты. Тут аналогично Началъным моментом порядка (к, 1} называется математическое ожидание функции хку':

vkJ M (X kY l )

vkJ xk yl fX ,Y (x, y)dxdy

M ( XY ) xy fX ,Y (x, y)dxdy

(1)

Центральным моментом порядка (к, Г) называется математическое ожидание функции (х-mx) \y-my) ,где mx = E(Х), my = E{Y):

32

k ,l (x mx )k ( y mY )l fX ,Y (x, y)dxdy

101.Каков смысл начальных и центральных моментов двумерного случайного вектора (X,Y)?Ответ обоснуйте.

Первые начальные моменты – это математические ожидания случайных величин Х и У.

Точка с координатами (E(Х),E(У)) характеризует центр системы случайных величин, вокруг которого происходит рассеивание возможных значений. Кроме первых моментов широко используют вторые центральные моменты, которые бывают трех типов. Два из них дают дисперсии компонент Х и У:

величин X и 7 вдоль осей х и у.

Особую роль в определении взаимодействия компонент играет второй смешанный центральный момент

1,1 M ( XY )

102.Дайте определение корреляционной и ковариационной матриц для системы случайных величин Х1,Х2…Хn и сформулируйте их основые свойства.

Для набора случайных величин X1, X2, …, Xn ковариационной матрицей C=(cij) и корреляцион-

ной матрицей R=(pij)называют квадратные матрицы порядка n, составленные из всех парных ковариаций cij=cov(Xi, Xj) и всех коэффициентов корреляции pij=p(Xi,Xj), I,j=1,…,n

Основные свойства:

1.Ковариационная и корреляционная матрица являются симметричными матрицами

2.Ковариационная и корреляционная матрица неотрицательно определены

3.Определители этих матриц неотрицательны. detR<=1

103.Как найти ковариацию Сov(X,Y) случайных величин X и Y , если известна функция плотности fX ,Y (x, y)

двумерного распределения (X;Y)? Верно ли, что из равенства Сov(X,Y)=0 вытекает независимость X и Y , если (X;Y) – двумерный нормальный случайный вектор?

Ковариацией или корреляционным моментом случайного вектора (X, Y) называют величину

Cov(X,Y)=E((X-mx)*(Y-my))=∫∫-∞∞(x-mx)(y-my)f(x,y)dxdy, где mx=E(X), my=E(Y)

Ковариация обладает следующими свойствами:

1. СОV(Х, Y) = M(XY) - M(X)M(Y).

2.СОУ(Х, X) = D(X).

3.D(X+Y) = D(X) + D(Y) + 2Cov(X, Y).

4.Если X и Y независимы, то Cov(X, Y) = 0.

5.Cov(X, Y) = Cov(Y, X).

6.Cov(aX,Y) = Cov(X,aY) = aCov(X, Y).

7.Coy(X+Y, Z) = Cov(X, Z) +Coy(Y,Z).

8.Cov(X, Y+ Z) = Cov(X, Y) + Cov(X, Z).

Если Cov(X, Y) = 0, то случайные величины X и Y называются некоррелированными. Таким образом, согласно свойству 4 из независимости X и Y следует их некоррелированность. Обратное утверждение неверно.

104. Укажите формулу для плотности распределения случайной величины Y +X= Z , если ( X,Y) – двумерный случайный вектор с функцией плотности f(x,y) и независимыми компонентами X и Y . Приведите пример ее применения.

33

если даны 2 независ. случ. величины Х и У, распределённые равномерно соответственно на отр-ках [0,m] и [0,n] (m<=n), то можно найти функцию плотности Z=X+Y.

Z сосредоточена на отр-ке [0,m+n], формула принимает вид

105. Как определяются условные законы распределения для дискретных случайных величин X и Y?

Мы можем найти зависимость СВ через условные законы распределения, т.е. закона распределения одной СВ, при условии, что др. СВ приняла определенное значение.

Если СВ X и Y дискретные, то их условные законы распр-я могут быть определены, используя теорию умножения

вероятностей P(X= xi | Y= yi )= P(X xi , Y yi ) , для всех yi , таких что P(Y yi ) >0 определяет усл.

P(Y yi )

распределение ДСВ x, при условии X xi .

P(Y= yi | X= xi )= P(X xi , Y yi ) , для всех xi , таких что P(X xi ) >0 опред. условие распр-е ДСВ y, при

P(X xi )

условии Y yi .

106 Сформулируйте определение условной ф-ии распр СВ Х при усл Y=y. Как определяется условная плотность f(y|x) распределения? Чему равна f(y|x), если СВ X и Y независимы?

Набор вероятностей fx|y(xk|yk)=P(X=xk|Y=yl)={P(X=xk,Y=yl)}/P(Y=yl) для всех yl, таких, что P(Y=yl)>0 определяет условное распределение дискретной СВ Х при условии Y=yl. Аналогично для определения условного распр Y при условии X=xk. Если X и Y независимы, то fX|Y(xk|yy)=fX(xk); fY|X(yl|xk)=fY(yl).

107. Как определяется условное математическое ожидание непрерывной случайной величины Y при условии X = x и математическое ожидание случайной величины X при условии Y = y? Докажите, что M(M(X |Y))= M(X )

и M(M(Y | X ))= M(Y).

Определение. Условным математическим ожиданием случайной величины Y при условии, что случайная величина X приняла значение x, называется величина

34

.

Аналогично определяется условное математическое ожидание X при условии, что Y = y

.

Заметим, что, вообще говоря, условное математическое ожидание, определенное формулой (7.41), не является числом, а выражается в виде некоторой функции, зависящей от x. Более того, каж-дую из функций (7.41), (7.42) можно рассматривать соответственно как функцию от случайной вели-чины X и Y. Поэтому можно найти их математическое ожидание

Сформулируем полученное соотношение в виде теоремы. Теорема 7.3. Выполняются следующие соотношения

Если не прибегать к излишней строгости, соотношения (7.43) и (7.44) можно выразить словами: «Математическое ожидание от условного математического ожидания дает математическое ожидание исходной величины».

108.Сформулируйте и докажите неравенство Чебышева.

Неравенство Маркова: если x 0, a>0, то P(X a) M(X)/a

Н-во Чебышева: пусть X – СВ, у кот есть M(X)=m и D(X)=a, тогда >0 справедливо н-во

P(|X-m| ) D(X)/ 2 Док-во: P(X ) m/ - н-во Маркова. |X-m| ; (X-m)2/ 2 1; P(|X-m| ) = P((X-m)2/ 2 1) M((X-m)2/ 2) = 1/ 2 M((X-m)2) = D/ 2; P(|X-m| ) D(X)/ 2.

109.Используя н-во Чебышева, сформулируйте и док-те «правило трех сигм» для произвольной СВ X.

Н-во Чебышева: пусть X – СВ, у кот есть M(X)=m и D(X)=a, тогда >0 справедливо н-во

P(|X-m| ) D(X)/ 2. Противоположное событие: 1 - P(|X-m| ) 1 - D(X)/ 2; P(|X-m|< ) 1 - D(X)/ 2. Правило 3 : Пусть =3 : P(|X-m|<3 ) 1- 2/9 2 = 8/9.

110.Сформулируйте и докажите теорему Чебушева для бесконечной последовательности случайных величин с одинаковыми математическими ожиданиями и дисперсиями, ограниченными одним и тем же числом.

1°. Теорема Чебышева. Неравенство Чебышева позволяет доказать ряд важных теорем, объе-диненных одним общим названием "закон больших чисел". Основная из этих теорем принадлежит самому П.Л. Чебышеву.

Теорема 10.1. (теорема Чебышева). Пусть имеется бесконечная последовательность X1, X2, …

независимых случайных величин с одним и тем же математическим ожиданием m и дисперсиями, ограниченными одной и той же постоянной:

Тогда, каково бы ни было положительное число , вероятность события

стремится к единице при

Доказательство. Положим,

.

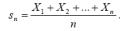В силу свойств математического ожидания имеем:

.

Далее, так как величины независимы, то

35

.

Сопоставив полученное неравенство с неравенством Чебышева:

,

будем иметь:

Это показывает, что с ростом n вероятность события стремится к 1.

Смысл теоремы Чебышева можно пояснить следующим примером. Пусть требуется измерить некоторую физическую величину m. В силу неизбежных ошибок результат измерения будет случай-ной величиной. Обозначим эту величину X; ее математическое ожидание будет совпадать с измеряе-мой величиной m, а дисперсия равна некоторой величине D (характеризующей точность измеритель-ного прибора). Произведем n независимых измерений и обозначим:

X1 – результат первого измерения;

X2 – результат второго измерения

и т.д. Совокупность величин X1, X2, …, Xn представляет собой систему n независимых случайных ве-личин, каждая

из которых имеет тот же закон распределения, что и сама величина X. Среднее ариф-метическое этих величин тоже является, конечно, случайной величиной. Однако с увеличением n эта величина почти перестает быть случайной, она все более приближается к постоянной m. Точная количественная формулировка этой близости

состоит в том, что событие становится как угодно достоверным при достаточно большом n.

Тем самым оправдывается рекомендуемый в практической деятельности способ получения бо-лее точных результатов измерений: одна и та же величина измеряется многократно, и в качестве ее значения берется среднее арифметическое полученных результатов измерений.

Близость к M(X) среднего арифметического опытных значений величины X уже подчеркивалась нами при самом введении понятия математического ожидания. Однако соответствующее рассуждение относилось только к дискретным случайным величинам; кроме этого, само высказывание о близости мотивировалось соображениями эмпирического характера. В противоположность этому теорема Че-бышева дает точную характеристику близости среднего арифметического к M(X) , и притом для любой случайной величины.

111 Сформулируйте и докажите теорему Бернулли (закон больших чисел).

Если в каждом из п независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.

Другими словами, если - сколь угодно малое положительное число, то при соблюдении условий теоремы имеет

место равенство lim P(| m / n p | 1. Доказательство. Обозначим через Х1 дискретную случайную величину—

n

число появлений события в первом испытании, через Х2—во втором, ..., Хn—в n-м испытании. Ясно, что каждая из величин может принять лишь два значения: 1 (событие А наступило) с вероятностью р и 0 (событие не появилось) с вероятностью 1—р=q. Можно ли применить к рассматриваемым величинам теорему Чебышева? Можно, если случайные величины попарно независимы и дисперсии их ограничены. Оба условия выполняются. Действительно, попарная независимость величин X1, Х2, . . ., Хn следует из того, что испытания независимы. Дисперсия любой величины Xi (i= 1, 2, . .., n) равна произведению pq, так как p+q=1,то произведение pq не превышает 1/4 и, следовательно, дисперсии всех величин ограничены, например, числом С =1/4. Применяя теорему Чебышева

(частный случай) к рассматриваемым величинам, имеем lim P(| ( X1 X 2 ... X n ) / n a | ) 1. Приняв во

n

внимание, что математическое ожидание а каждой из величин Xi (т. е. математическое ожидание числа появлений

Остается показать, что дробь (X1+X2+…Xn)/n равна относительной частоте т/п появлений события А в испытаниях. Действительно, каждая из величин X1,X2,…Xn при появлении события в соответствующем испытании принимает значение, равное единице; следовательно, сумма X1+X2+…+Xn равна числу m появления события в n испытаниях, а значит, (X1 X 2 ... X n ) / n m / n. Учитывая, это равенство, окончательно получим

36

lim P(| m / n p | 1. Итак, теорема Бернулли утверждает, что при n относительная частота стремится по

n

вероятности к p.

112. Сформулируйте центральную предельную теорему. Укажите примеры ее применения.

ЦПТ для одинаково распределенных СВ: Пусть X1…Xn – последовательность независимых одинаково распределенных СВ M(X1)=…=M(Xn)=m<+ ; D(X1)=…=D(Xn)= 2<+ , тогда закон распр СВ

Sn = (x1+…+xn – nm)/√n , тогда Sn стремится к стандартному нормальному закону при n→

Применение: При измерении какой-либо физ величины на результат влияет огромное кол-во факторов. Каждый из этих факторов порождает ничтожную ошибку Xk. Результирующая ошибка Sn будет суммой величин Xk, то есть вся сумма Sn будет иметь закон распределения, близкий к нормальному. Сл-но, случайная ошибка измерения подчиняется нормальному закону распр: мат ожидание равно нулю, среднее квадратич откл – характеризует точность измерения. Др. пример: массовое производство. Изготовляются большие партии однотипных изделий, где каждое должно соответствовать стандарту. Но есть отклонение от стандарта, кот порождаются причинными случайного хар-ра (Xk). Sn имеет норм распр.

113. Сформулируйте центральную предельную теорему для одинаково распределенных случайных величин и приведите пример ее применения.

Если x1 , … xn - последовательность независимых случайных величин, имеющих один и тот же закон распределения с математическим ожиданием m и дисперсией б2 , то при неограниченном увеличении n закон

распределения нормализованной суммы 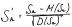неограниченно приближается к нормальному.

114. Используя центральную предельную теорему, обоснуйте интегральную формулу Лапласа.

Если Х – случайная величина, явл-ся суммой большого числа независимых случайных величин, то случайная величина Х-МХ/ςх имеет распределение, близкое к стандартному нормальному, т.е.

Где Хi=0, если в i-ом успеха не было, 1, если успех был. Р{α≤(X-np)/√npq≤β}= Ф(β)-Ф(α)

Р{np+α√npq≤x≤np+β√npq}

115. Как вводятся основные характеристики статистической совокупности (выборки): среднее, дисперсия, центральные моменты высших порядков, асимметрия, эксцесс? Какие из перечисленных характеристик остаются неизменными при линейных преобразованиях x → ax + b?

Определение. Центральным моментом порядка k (k е N) случайной величины X называют математическое ожидание k-й степени отклонения = X – m, где m – математическое ожидание X:

Для дискретных случайных величин формула для центрального момента порядка k выглядит следующим образом:

для непрерывных случайных величин

37

Определение. Асимметрией распределения называют отношение третьего центрального момента к кубу стандартного отклонения:

Замечание. Асимметрия случайной величины X совпадает с третьим начальным (центральным) моментом соответствующей нормированной случайной величины.

Действительно, по определению

Определение. Эксцессом распределения называется величина

Поскольку для стандартного нормального распределения N(0, 1) мы нашли, что μ4 = 3 (см. (6.22)), то для

нормального распределения эксцесс равен нулю. В частности, вычисляя эксцесс неизвестного распределения, мы можем судить о близости его к нор-мальному по этой числовой характеристике.

Для биномиального закона

Действительно, воспользуемся формулой (6.18). Имеем

дится ниже и носит название дисперсии.

Определение. Дисперсией случайной величины X называется число

Другими словами, дисперсия есть математическое ожидание квадрата отклонения. Из определения (4.8) легко вытекают следующие свойства дисперсии.

остаются неизменными при линейных преобразованиях x → ax + b Дисперсия, асимметрия, эксцесс Проблемя, найдите определение средней!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

116 Сформулируйте определение выборочной (эмпирической) функции распр для СВ Х. Как связаны ф-ии распределения признака в генеральной и выборочной совокупностях?

распределения, при этом она кусочно-постоянна.

Случ выборкой объема n из ген совокупности X называется случ вектор Zn=(X1…Xn), компоненты которого являются независимыми СВ, распредел так же как и X. Реализацией выборки называется вектор Zn=(X1,…Xn), его компоненты xn – реализацией Xk. Мн-во S всех реализаций выборки Zn называется выборочным пространством.

117. Каким образом на рисунках изображаются выборочные распределения непрерывных и целочисленных случайных величин? Что такое полигон частот? Как строится гистограмма относительных частот? Чему равна сумма площадей столбиков диаграммы?

Хз как ответить на первый вопрос(в учебниках нет), наверное при помощи полигона и гистограммы.

Полигоном частот называют ломаную, отрезки которой соединяют точки (х1; п1), (х2; п2), ..., (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат — соответствующие им частоты ni. Точки (хi; пi) соединяют отрезками прямых и получают полигон частот.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению Wi/h (плотность относительной частоты).

38

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии W{/h. Площадь i-го частичного прямоугольника равна hWi/h=Wi—относительной частоте вариант, попавших в i-й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т. е. единице

118.Сформулируйте понятие несмещенной точечной оценки. Будет ли оценка математического ожидания m, построенная по результатам двух измерений X1и X2 в форме m=1/10X1+(1-1/10)X2, несмещенной оценкой m?Ответ обоснуйте.

Несмещенной точечной оценкой называют оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.

ˆn ˆ( X1...Xn ) параметра называется несмещенной, если M ( ˆn ) . В противном случае оценка – смещенная. mˆ 101 X1 (1 101 ) X 2 - является ли несмещенной оценкой?

mˆ 101 X1 (109 ) X 2

M (mˆ ) 101 M ( X1 ) 109 M ( X 2 ) 101 m 109 m m

119.Сформулируйте понятие несмещенной, состоятельной и эффективной оценки параметра генерального распределения. Приведите примеры.

неизвестные параметры. Функцию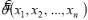, которая при фиксированных значениях принимает значение, рассматриваемое как приближенное зна-чение неизвестного параметра θ генерального распределения, называют статистической оценкой па-раметра θ. По определению оценка является несмещенной, если ее математическое ожидание равно оцениваемому параметру. Эффективной называют оценку, которая при заданном объеме выборки п имеет наименьшую возможную дисперсию. Наконец, оценка называется состоятельной, если при она стремится (по вероятности) к оцениваемому параметру.

Выборочное среднее

является состоятельной и несмещенной оценкой для генерального среднего. Выборочная дисперсия

является состоятельной, но смещенной оценкой дисперсии. Статистическая оценка

называемая исправленной дисперсией, является состоятельной несмещенной оценкой генеральной дисперсии.

120.Докажите, что для генерального распределения с математическим ожиданием m и конечной дисперсией σ2 выборочное среднее является несмещенной и состоятельной оценкой m.

Выборочное среднее ¯x=1/n*Σxn является несмещённой состоятельной оценкой математического ожидания m. Док-во. Поскольку каждая из величин генеральной выборки имеет математическое ожидание M(X), математическое ожидание выборочного среднего ¯ M(X)= 1/n*Σ M(Xi) = M(X), т.е выборочное среднее является несмещённой оценкой. В силу независимости величин выборки D¯x=1/n2*ΣD(Xi)=D(x)/n. Состоятельность докажем с помощью нер-ва Чебышева для выборочного среднего с учётом несмещённости: ρ(׀¯x - M(X)׀>= ε) <= D(¯x) / ε2 = D(x)/n ε2 для всякого ε>0. Поэтому limn→∞ ρ(׀¯x - M(X)׀>= ε)=0. Отсюда limn→∞ ρ(׀¯x - M(X)׀< ε)= 1 - limn→∞ ρ(׀¯x - M(X)׀>= ε) = 1.

Пусть Zn = (x1…xn) – случ выборка объема n, тогда исправленной выборочной дисперсией называется величина

122. Выведите формулу для дисперсии выборочного среднего бесповторной выборки.

В случае простой бесповторной выборки x1…xn мат ожидание и дисперсия выборочного среднего опр по формулам

M( x )=m D( x )= 2/n * (N-n)/(N-1).

Док-во: 1) M( x ) = M ((x1+…+xn)/n) = 1/n (m+…+m)=m.

2)D((x1+…+xn)/n)=1/n2 * D(x1+…+xn) = 1/n2 * {D(x1)+...+D(xn) + 2 Cov(xi x j ) } = 1/n2 (n 2+2C2n*C)=

i j

= 1/n2 (n 2+2*{n(n-1)/2}*C)=1/n ( 2+(n-1)C) ====

Рассм. случ выборку, сост из элементов ген совокупности (n=N), тогда x - не случ величина, а константа, сл-но, при

n=N D( x )=0=1/N ( 2+(N-1)C), сл-но, C = - 2/(N-1)

==== 1/n ( 2+(n-1)* {- 2/(N-1)}) = …

123. Что такое интервальная оценка для параметра при доверительной вероятности ? Какой практический смысл имеет такая оценка, если близка к 1? Как изменится доверительный интервал при

уменьшении доверительной вероятности?

Пусть - неизвест пар-р или числовая хар-ка ген распр. Если выполняется P(| ˆ | ) j , то интервал I j ( ˆ ; ˆ ) - называется доверительным интервалом, который покрывает неизвестный пар-р ген

распределения с доверительной вероятностью (надежность оценки); - точность оценки.

Если близка к 1, то такая оценка является надежной. При уменьшении , тоже уменьшается, значит, чтобы точно попасть в интервал его надо развинуть.

124. Пусть n X , X , ..., X 1 2 – выборка из нормального распределения с математическим ожиданием m и дисперсией σ 2. Докажите, что для t > 0 интервал накрывает m с вероятностью 2 Ф (t), где Ф (t) – функция Лапласа.

Пусть X1, ..., Хn – выборка из нормального распределения Х с параметрами: M(X)=m, D(X)=σ2

тогда для t>0 доверит. интерв. (X-tσ/√n; X+tσ/√n), где x – выб. сред., а t – реш-е ур-ния Ф(t) = j/2, к-рый накрывает неизв. параметр m c над-тью j с вер-тью 2Ф(t), т.е. 2Ф(t)=j

Док-во:

Связь между надежностью j и точностью оценки σ. По данному j найдем σ, так чтобы P( x -m<σ)=J

X~N(m, σ2), x ~N(m, σ2/n)

P( x -m<σ)=P(m-σ< x <m+σ)=Ф(σ/√ σ2/n)-Ф( σ/ √σ2/n)=2Ф(σ√n/ σ)=j, где σ√n/ σ=t => 2Ф(t)=λ

125

126 Укажите приближенный γ -доверительный интервал для доли признака в генеральной совокупности по относительной частоте. При каких n формула дает хорошее приближение?

Пусть р - доля признака генеральной совокупности, k/n-выборочная доля, тогда доверительный интервал равен:

40