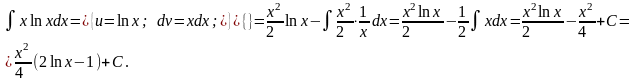- •Дайте опр-я ф-и, а также сложной и обратной ф-й одной действительной переменной. Найдите обл опр и обл значений функции .
- •Сформулируйте св-ва четности, нечетности, периодичности, монотонности, ограниченности ф-и. Определить явл-ся ли след ф-я четной или неч.
- •Дайте определения числовой посл-ти и предела числовой посл-ти. Сфор-те теорему о единственности предела числовой посл-ти.
- •Переч правила вычисления пределов посл-тей. Дайте определение числа e.
- •Дайте определение предела функции. Перечислите основные свойства пределов функций.
- •Дайте определения односторонних пределов функции.
- •Перечислите основные правила вычисления пределов функций.
- •Приведите первый (с доказательством) и второй замечательные пределы.
- •Дайте опр непрерывности ф-и в точке. Сформ-те условия непрерывности сложной ф-и. Что вы можете сказать о непрер-ти основных элем ф-й?
- •Перечислите основные локальные свойства непрерывных функций.
- •Сформ теорему о сущ-и корня уравнения для ф-и , непрерывной на отрезке. Докажите, что уравнение имеет корень на отрезке .
- •Сформ теорему о существовании и непрерывности ф-и, обратной к строго монотонной непр ф-и. Приведите пр-р и обоснуйте его на основании теоремы.
- •Сформулируйте свойства функций, непрерывных на отрезке: об ограниченности функции, о достижении наибольшего и наименьшего значений.
- •Дайте опр производной ф-и в точке. На основании опр-я найди производную ф-и .
- •Приведите правила дифференцирования суммы, разности, произведения и частного двух функций, Докажите одно из них на выбор.
- •Приведите правила дифференцирования сложной и обратной функции. Найдите производную функции согласно сформулированному правилу.
- •Дайте определение производных высших порядков ф-и одного аргумента. Приведите примеры вычисления таких производных.
- •Сформулируйте с обоснованием ответ на вопрос: в чем состоит связь между дифференцируемостью и непрерывностью функции?
- •Обоснуйте возможность использования дифференциала в приближенных вычислениях. Приведите пример.
- •Сфор-те теоремы Лагранжа и Коши для дифференцируемых ф-й. Проверьте справедливость теоремы Лагранжа для функции на отрезке .
- •Сформ теоремы Лагранжа и Коши для дифференцируемых ф-й. Проверьте справедливость теоремы Лагранжа для функции на отрезке .
- •Сформ теоремы Ферма и Ролля для дифференцируемых функций. Проверьте справедливость теорема Ролля для функции на отрезке .
- •Сформулируйте правило Лопиталя. Докажите первый и второй замечательные пределы с помощью правила Лопиталя.
- •Дайте определения возрастающей и убывающей функций. В чем состоит необходимое и достаточное условия локального экстремума функции.
- •Дайте определения выпуклых вниз и вверх функций одного аргумента. Приведите достаточные условия выпуклости функции. Приведите примеры.
- •В чем состоит необх и дост признаки точки перегиба графика функции. Приведите пример.
- •Дайте опр-я ф-и двух переем-ых, предела и непрерывности ф-и двух переем-х.
- •Дайте определения частных производных ф-и двух переменных, дифференцируемости ф-и нескольких переем-х и ее дифференциала. Приведите примеры вычисления производных и диф-ла ф-и двух пременных.
- •Дайте опр-я производной по напр-ю и градиента ф-и двух перем. ВчемСостоитОсновное св-о градиента ф-и.
- •Сформулируйте теорему о наибольшем и наименьшем значениях дифференцируемой функции на замкнутом ограниченном множестве. Приведите пример.
- •Дайте опр- частных производных высших порядков ф-и двух перем. Сформ теорему о равенстве смешанных производных и приведите в качестве ее иллюстрации пример.
- •Дайте опр экстремума функции двух переменных. В чем состоит необходимое и достаточное условия экстремума. Проиллюстрируйте это на примере.
- •Дайте опр-я условных максимума и минимума функции двух переменных. В чем состоит метод множителей Лагранжа для нахождения условных максимума и минимума функции двух переменных. Приведите пример.
- •Дайте опр однородной ф-и двух аргументов и сфор теорему Эйлера. Явл-я ли ф-я однородной, и если да, то какова степень одн-ти?
- •Дайте определение выпуклой функции двух аргументов и приведите критерий выпуклости. Проиллюстрируйте это на примере.
- •Дайте определение и перечислите основные свойства неопределенного интеграла, иллюстрируя их примерами.
- •Сформулируйте теорему о замене переменной в неопределенном интеграле и правило интегрирования по частям. Докажите любое из этих двух утверждений.
- •Дайте определение и приведите пример первообразной. Сформулируйте теорему о существовании первообразной для непрерывной функции.
- •Напишите формулы вычисление площади криволинейной трапеции и объема тела вращения. Приведите в обоснование чертежи к каждой из формул и приведите примеры.
- •Дайте определения несобственных интегралов с бесконечными пределами. Приведите примеры вычисления таких интегралов.
- •Сформулируйте определения числового ряда и его суммы. В чем состоит достаточный признак сходимости ряда. Гармонический ряд.
- •Сформулируйте определения и приведите признаки сходимости положительных и знакочередующихся рядов. Проиллюстрируйте это на примерах.
- •Дайте опр степ ряда и обл его сх-ти. Приведите фор-лу для выч-я радиуса сх-ти степ ряда.
Дайте определение выпуклой функции двух аргументов и приведите критерий выпуклости. Проиллюстрируйте это на примере.
Множество
называется выпуклым,
если вместе с любыми своими точками
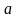 и
и
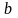 оно целиком содержит отрезок
оно целиком содержит отрезок
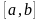 .
Функция, заданная на выпуклом
множестве, будет выпуклой вниз, если
все точки поверхности, заданной этой
функцией, соответствующие отрезку
множества В,
лежат не выше хорды, соединяющей точки
.
Функция, заданная на выпуклом
множестве, будет выпуклой вниз, если
все точки поверхности, заданной этой
функцией, соответствующие отрезку
множества В,
лежат не выше хорды, соединяющей точки
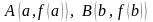 (рис. 12). Анал-но можно дать геом-ое
толкование вып вверх ф-и двух переменных.
(рис. 12). Анал-но можно дать геом-ое
толкование вып вверх ф-и двух переменных.
О чевидно,
выпуклая ф-я не может иметь седловых
точек (точек перегиба). Это зн-ит, что
для вып ф-и рав-во нулю частных производных
явл-я не только необ усл экс-, но и дост.
чевидно,
выпуклая ф-я не может иметь седловых
точек (точек перегиба). Это зн-ит, что
для вып ф-и рав-во нулю частных производных
явл-я не только необ усл экс-, но и дост.
Более того, экстремум выпуклой ф-и явл-ся глобальным, то есть наим-м зн-ем во всей области определения в случае функции, выпуклой вниз, и наиб-им в случае функции, выпуклой вверх.
Теорема.
Если ф-я
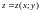 выпукла
(вогнута) во всей обл определения D,
тогда она имеет не более одной точки
глобального минимума (максимума) в
области D.
выпукла
(вогнута) во всей обл определения D,
тогда она имеет не более одной точки
глобального минимума (максимума) в
области D.
Пример:
Исследовать на выпуклость и вогнутость:
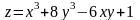
Найдем
критические точки:
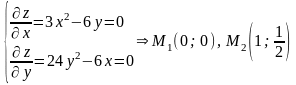
Исследуем
эти точки, для этого найдем частные
производные:
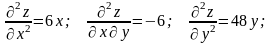
Исследуем точку M1: а) А=6х (М1=0), В= –6 (М1= –6), С=48у (М1=0)
∆(М1)=АС –В2= –36 < 0. В точке М1 нет экстремума, т.к. ∆<0.
Исследуем точку M2: б) А=6х (М2=6), В= –6 (М2= –6), С=48у (М2=24)
∆(М2)=108 > 0. Т.к. значение A>0, значит в точке М2 минимум (zmin=0). Ф-я выпукла.
Дайте определение и перечислите основные свойства неопределенного интеграла, иллюстрируя их примерами.
Определение: Если F(x) – первообразная для f(x),то выражение F(x) + C, где С – произволь пост-ая, наз-ся неопределенным интегралом от ф-и f(x).
Записывают:
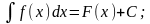
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:1.
 Пример
Пример
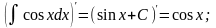
2.
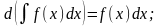 Доказательство:
Доказательство:

Пример
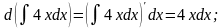
3.
 Пример
Пример
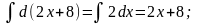
4.
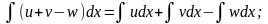 где u,
v,
w
– некоторые функции от х.
где u,
v,
w
– некоторые функции от х.
Док-во: Это вытекает из того, что если ф-и U, V и W – первообразные соот-но для u, v и w, то производная их суммы (разности) будет равна сумме (разности) производных.
Пример
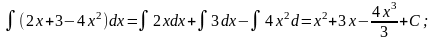
5.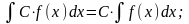 Пример
Пример
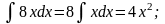
Сформулируйте теорему о замене переменной в неопределенном интеграле и правило интегрирования по частям. Докажите любое из этих двух утверждений.
Замена переменной
Теорема:
Пусть ф-я x
= (t)
определена и диф-ема на промежутке Т и
Х – мн-во ее зн-й, на кот определена ф-я
f(x).
Тогда если F(x)
– первообразная f(x)
на Х, то F((t))
- первооб для f((t))
(t)
на Т, т.е. на множестве Т выполняется
ра-во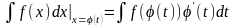
Док-во: По правилу диф-ия сложной ф-и производная левой части равенства равна:
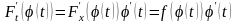
Что совпадает с подынтегр ф-ей в правой части рав-ва, это и док-ет рав-во. Т-ма док-на.
Пример.
Найти неопределенный интеграл
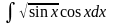 .
.
Сделаем замену t = sinx, dt = cosxdt.
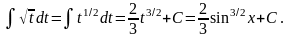
Интегрирование по частям.
Пусть
u(x)
и v(x)
– две дифференцируемые функции на
промежутке Х. Тогда на Х выполняется
формула интегрирования по частям: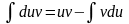
Док-во Имеем фор-лу для диф-ла произведения ф-й uv: d(uv) = udv + vdu
Проинт-в
обе части рав-ва, получаем:
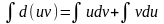 ,
а в соотв-и с прив-ми выше св-ми неопр-го
интеграла:
,
а в соотв-и с прив-ми выше св-ми неопр-го
интеграла: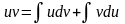 или
или
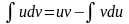 ;
;
Получили фор-у инте-ия по частям, кот позв-ет нах-ть инт-лы мн-их элем ф-й.
Пример: