21. Дайте определение производных высших порядков ф-и одного аргумента. Приведите примеры вычисления таких производных.

Пусть ф-я f(x) диф-ема на некот интервале. Тогда, диф-уя ее, получаем первую производную

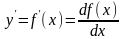
Если найти производную функции f(x), получим вторую производную функции f(x).

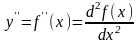_,т.е. y = (y) или .

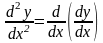Этот процесс можно продолжить и далее, находя производные степени n. .

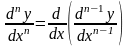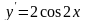
Пример 1. y = sin 2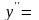x –4 sin2x 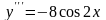_итд

Пример 2: (x^1/2) ' = ½ x ^{- 1/2} (x^1/2) ⁽²⁾ = -(1/2)² *x ^{– 3/2} (x^1/2) ⁽³⁾ = (1/2)³ * 3x ^{– 5/2} (x^1/2) ⁽⁴⁾ = -(1/2)⁴ *3 *5*x ^-7/2 (x^1/2) ⁽ⁿ⁾ = -(-1/2)ⁿ *3*5*7*...*(2n - 3)* x ^{–(2n-1) / 2}

22. Сформулируйте с обоснованием ответ на вопрос: в чем состоит связь между дифференцируемостью и непрерывностью функции?

Рассмотрим следующие вопросы, который касаются функций:

а) Если функция непрерывна, то она дифференцируема?

б) Если функция дифференцируема, то она непрерывна?

Ответ на первый вопрос: из непрерывности функции не следует ее дифференцируемость.

Ответ на второй вопрос: из дифференцируемости ф-и следует ее непрерывность.

Рассмотрим более конкретно каждый вопрос. Чтобы ответить на данные вопросы необ-мо док-ть озвученый факт или привести пример, кот опровергает этот факт.

Найдем производную следующей функции 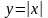 . Хорошо известно, что данная функция является непрерывной и что ее производная будет следующей:

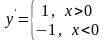
Покажем, что в точке нуль производная не существует. Для этого найдем производную в нуле по определению производной:

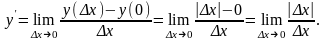Данный предел равен 1, если ∆х→0+ и равен (–1), если ∆х→0–, получается что предел не существует, следовательно в нуле производной нет и функция в нуле не дифференцируема.

23. Обоснуйте возможность использования дифференциала в приближенных вычислениях. Приведите пример.

Дифференциалом функции называется величина

dy= f ′ (х)dх

Рассмотрим подробнее формулу ∆ydy или f ′ (х₀+∆х) – f(х)  f ′ (х) ∆х; т.е.

f ′ (х₀+∆х)  f ′ (х₀) ∆х + f ′(х₀) – расчётная формула Эйлера;

Найдём

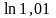
Полагаем y = f(x) =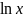 ; х₀ = 1, ∆х = 0,01 и y = f ′ (х) = 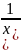, согласно расчётной формуле:

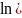
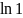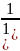 + * 0,01  0,01

2 способ Дифференциалом функции в точке х₀ называется линейная относительно приращения аргумента часть приращения функции в этой точке, эквивалентная всему приращению.

df(х₀)= f ′ (х₀) ∆х; ∆х=dх; df(х₀)= f ′ (х₀)dх

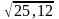
24. Сфор-те теоремы Лагранжа и Коши для дифференцируемых ф-й. Проверьте справедливость теоремы Лагранжа для функции на отрезке .

Теорема Коши:

Пусть ф-ции и 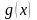непрерывны на отрезке [a;b], дифференцируемы на интервале (a;b) и 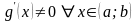, тогда существует точка 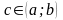такая, что .

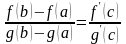Домножим левую часть уравнения на

Получили т-му Лагранжа. Теорема Лагранжа – это частный случай т. Коши, когда .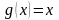

Теорема Лагранжа:

Пусть функция непрерывна на отрезке [a;b], дифференцируема на интервале (a;b), то существует точка такая, что .

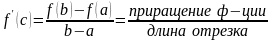Следствие 1: Если производная y=f(x) равна 0 на X, то для всех x  Х выполняется f=const.

Следствие 2: Правило Лопиталя ₀:

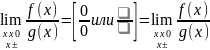
Проверьте справедливость теоремы Лагранжа для функции f (х) =1 - 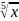⁴ на отрезке :

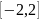y=1-(x⁴)^1/5 ; f(-2) = 1-(-2⁴)^1/5 = f(2)

В итоге: f ’(c)=0

Найдём f ’(x)=(1-(x⁴)^1/5)’ = -4/5 *x^-1/5=-4 / 5*x^1/5  0

Следовательно теорема Лагранжа не выполняется.