terve_teoria
.pdf№10
Закон Пуассона задается таблицей:
|
2 |
3 |
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
-λ -λ |
2! |
3! |
|
|
|
|
|
e |
|
|
|
|
|
|
|
Отсюда имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
M ( X ) k |
k |
e e |
|
|
e e = |
||
k ! |
(k 1)! |
||||||
|
k 0 |
|
k 1 |
|
|||
Таким образом, параметр λ, характеризующий данное пуассоновское распределение, есть не что иное как математическое ожидание величины X.
№11
Математическим ожиданием дискретной случайной величины с законом
распределения |
|
|
|
x1 |
x |
… |
называется число M(XY)= x1p1+ x2p2 + … |
2 |
|
|
|
p1 |
p |
… |
|
2 |
|
|
|
Если случайные величины X и Y независимы, то математическое ожидание их произведения равно произведению их математических ожиданий (теорема умножения математических ожиданий).
Доказательство: Возможные значения X обозначим x1, x2, …, возможные значения Y - y1, y2, … а pij=P(X=xi, Y=yj). Закон распределения величины XY будет выражаться
соответствующей таблицей. M(XY)= xi yj pij Ввиду независимости величин X и Y
i, j
имеем: P(X= xi, Y=yj)= P(X=xi)
данное равенство в виде pij=risj Таким образом, M(XY)=
P(Y=yj). Обозначив P(X=xi)=ri, P(Y=yj)=sj, перепишем
xi yj ri sj |
= xi ri yj sj . Преобразуя полученное |
i, j |
i, j |
равенство, выводим: M(XY)=( xi ri |
)( y j sj ) = M(X)M(Y), что и требовалось доказать. |
i |
j |
№12 |
|
|
|
|
Математическим ожиданием дискретной случайной величины с законом |
||||
распределения |
|
|
|
|
x1 |
|
x |
… |
называется число M(XY)= x1p1+ x2p2 + … |
|
2 |
|
|
|
p1 |
|
p |
… |
|
|
2 |
|
|
|
|
|
|
|
Математическое ожидание суммы двух случайных |
величин равно сумме математических ожиданий слагаемых: M(X+Y)= M(X)+M(Y). |
||||
Доказательство: Возможные значения X обозначим x1, x2, …, возможные значения Y - |
||||
y1, y2, … а pij=P(X=xi, Y=yj). Закон распределения величины X+Y будет выражаться
соответствующей таблицей. M(X+Y)= (x y ) |
p . Эту формулу можно переписать |
|||||
|
|
|
i, j |
i |
j |
ij |
|
|
|
|
|
|
|
следующим образом: M(X+Y)= |
xi |
p y j pij . |
Первую сумму правой части можно |
|||
|
i, j |
ij |
i, j |
|
|
|
|
|
|
|
|
||
представить в виде (xi pij ) . Выражение |
pij есть вероятность того, что наступит |
|||||
i |
j |
|
|
|
j |
|
какое-либо из событий (X=xi, Y=y1), (X=xi, Y=y2), … Следовательно, это выражение равно
P(X=xi). |
|
Отсюда |
|
xi |
p xi P(X xi ) M ( X ) . |
Аналогично, |
|
|
|
|
i, j |
ij |
i |
|
|
|
|
|
|
|
|
||
y j p |
y j P(Y y j ) M (Y ) . В |
итоге имеем: M(X+Y)= |
M(X)+M(Y), что и |
||||
i, j |
ij |
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
требовалось доказать.
№13
№14
Определение: Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отклонений этих
величин: |
xy |
|
Cov( X ,Y ) |
. |
|
(X ,Y) |
|
1. |
|
|
|
|
|||||||
|
|
||||||||
|
( X ) (Y ) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
Доказательство: Рассмотрим случайную величину Z = Y X X Y . Вычислим ее |
|||||||||
дисперсию 2 (Z ) Y2 X2 |
2 X2 Y2 2 Y X Y X |
2 X2 Y2 (1 2 ) . Поскольку левая |
|||||||
часть неотрицательна, то правая неотрицательна. Следовательно, 1 2 0 , |ρ|≤1.
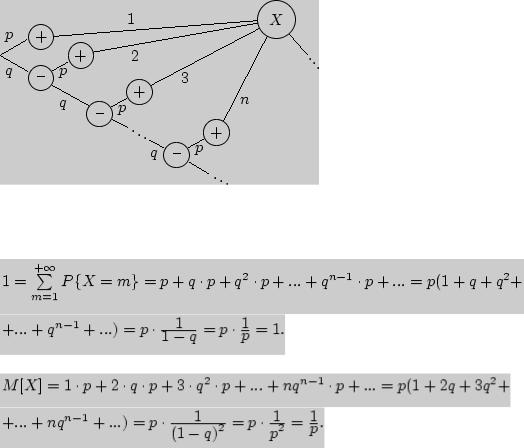
№15 1). Проводим повторные независимые испытания до появления "успеха". Граф
распределения в этом случае выглядит следующим образом.
Рис. 51
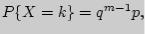где 
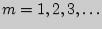Проверим, что
2). а). Математическое ожидание
ИЛИ
Вероятность появления события А в одномиспытании равна р, противопложного события q=1-p. Используф закон распределения случайной величины X запишем выражение дляматематического ожидания М(Х) = 1р+2pq+...+npqn-1+...=p(1+2q+3q2+...+nqn-1+...) Ряд записанныйв скобках, получается почленным дифференцированием геометрической прогрессии q+q2+q3+...+qn+... Следовательно М(Х) = р(1/(1-q)-1)=р(1/(1-q)2=р/р2=1/р.
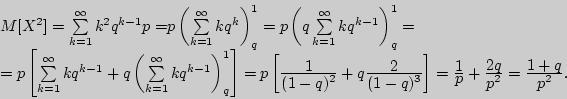
№16 3). Для вычисления дисперсии найдем
Тогда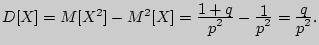 
ИЛИ
D(x)=M(x2)-M2(x), M(x2)=12p+22qp...=k2qk-1p=p(q+2q2=3q3+...)=p(q/(1-q2) Возьмем производную от выражения вскобкахи подставимвизначальноевыражение дисперсии, учитывая, что М(Х)=1/р. Получим D(x)=1-р/р2
№17
|
|
|
|
b |
|
|
Найдем математическое ожидание Х по формуле |
M ( X ) xf (x)dx. |
, учитывая, что плотность |
||||
|
|
a |
|
|||
|
b |
|
1 |
b |
|
|
|
M ( X ) xf (x)dx |
xdx |
|
|
||
равномерного распределения f(x)=1/(b-a): |
a |
|
b a a |
.Выполнив элементарные |
||
выкладки, получим M(X)=(a+b)/2.
|
b |
2 |
2 |
|
1 |
b |
2 |
a b 2 |
|
||
Найдем дисперсию Х: |
D( X ) x |
f (x)dx [M ( X )] |
|
|
x |
dx |
|
|
.Выполнив элементарные выкладки, |
||
|
|
||||||||||
a |
|
|
|
b a a |
|
|
2 |
||||
получим D(X)=(b-a)2/12.
№18
Объясните (с доказательством) вероятностный смысл параметра т в формуле для
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) 1 |
|
|
e ( x m)2 2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||
функции плотности |
случайной величины, распределенной |
|||||||||||||||||
|
|
|||||||||||||||||
по нормальному закону. |
|
|
|
|||||||||||||||
1 |
|
|
( x m)2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
f (x) |
|
|
|
e |
2 |
. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
( x m)2 |
|
|
|
|
||
Формула f (x) |
|
|
2 2 |
|
|
|
||||||||||||
|
|
|
|
e |
|
описывает плотность нормального распределения вероятностей |
||||||||||||
|
2 |
|
||||||||||||||||
непрерывной с.в..
Как видно, нормальное распределение определяется двумя параметрами: m и . Достаточно знать эти параметры, чтобы задать нормальное распределение. Докажем, что вероятностный смысл этих параметров таков: m есть математическое ожидание.
|
|
1 |
|
|
( x m)2 |
|
|
M ( X ) xf (x)dx |
|
|
2 2 |
|
|||
|
|
|
|
xe |
|
dx. |
|
|
|
2 |
|
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Введем новую переменную z (x m) / . Отсюда x z m, dx dz . Приняв во внимание, что
|
|
|
|
|
|
|
|
|
|
|
|
M ( X ) |
|
( z m)e z2 / 2dz |
|||||||
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
m |
|
|
|
ze z2 / 2dz |
|
e z2 / 2dz. |
||||||
|
|
|
|
|
||||||
новые пределы интегрирования равны старым, получим 2 |
|
|
|
|
|
2 |
||||
Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых
равно m (интеграл Пуассона e z2 / 2dz 
2 ).
Итак, M(X)=m, т.е. математическое ожидание нормального распределения равно параметру m.
№19
|
|
|
|
|
|
|
|
1 |
|
|
|
|
( x m)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
f (x) |
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Формула |
|
2 |
|
|
|
|
описывает плотность нормального распределения |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
вероятностей непрерывной с.в.. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Докажем, что - среднее квадратическое отклонение нормального распределения. |
||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
( x )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
D( X ) |
|
|
(x ) |
2 |
e |
|
|
2 2 |
|
dx. |
Введем новую |
переменную |
z=(х—μ)/ . Отсюда |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x z, dx dz .Приняв во |
внимание, |
что |
новые пределы интегрирования |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|||||
равны старым, получим |
D( X ) |
|
2 |
|
z ze z / 2dz. |
Интегрируя по частям, положив |
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u=z, dv ze z2 / 2dz, найдем |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
D( X ) 2 . |
Следовательно, ( X ) |
|
D( X ) |
2 |
|||||||||||||||||||||||||
.Итак, среднее квадратическое отклонение нормального распределения равно параметру.