terve_teoria

№20

Докажите, что для нормальной случайной величины с параметрами т и о функция распределения

произвести замену t-a/σ=z, то получим F{x)=1/2 + Ф(h-m/σ), где Ф(х) есть функция Лапласа

№21

№22

№23

Н-во Чебышева: Пусть X – СВ, у кот есть M(X)=m и D(X)=a, тогда >0 справедливо неравенство:

P(|X-m| ) D(X)/ 2

Доказательство: Неравенство является следствием другого неравенства, также принадлежащего Чебышеву: если СВ Х может принимать только неотрицательные значения (т.е. Р(Х<0)=0), то вероятность того, что принятое ею значение окажется меньше единицы, не превосходит числа m – математического ожидания Х:

P(X ≥ 1) ≤ m .

(m= a P( X a) a P( X a) a P( X a) (т.к. 1-ое слагаемое

a a 1 a 1

положительно, то если его убрать, будет меньше) a P( X a) (заменим a на 1, будет

a 1

только меньше) 1 P( X a) = P( X a) =P(X 1). Отсюда P(X ≥ 1) ≤ m .)

неотрицательные значения, то к ней можно применить доказанное выше неравенство:

конечном итоге P(|X-m| ) D(X)/ 2.

№24

Теорема Чебышева. Пусть имеется бесконечная последовательность X1, X2, …

независимых случайных величин с одним и тем же математическим ожиданием m и дисперсиями, ограниченными одной и той же постоянной:

Тогда, каково бы ни было положительное число , вероятность события

стремится к единице при 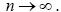Доказательство. Положим,

.

В силу свойств математического ожидания имеем:

.

Далее, так как величины независимы, то

.

Сопоставив полученное неравенство с неравенством Чебышева:

,

будем иметь:

Это показывает, что с ростом n вероятность события 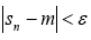стремится к 1.

№25

Если в каждом из n независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.

Другими словами, если - сколь угодно малое положительное число, то при

соблюдении условий теоремы имеет место равенство lim P(| m / n p | ) 1.

n

Доказательство. Обозначим через Х1 число появлений события в первом испытании, через Х2 – во втором, ..., Хn – в n-м испытании. Ясно, что каждая из величин может принять лишь два значения: 1 (событие А наступило) с вероятностью р и 0 (событие не появилось) с вероятностью 1—р=q. Все Х удовлетворяют условиям теоремы Чебышева. Действительно, попарная независимость величин X1, Х2, . . ., Хn следует из того, что испытания независимы. Дисперсия любой величины Xi (i= 1, 2, . .., n) равна произведению pq, так как p+q=1,то произведение pq не превышает 1/4 и, следовательно, дисперсии всех величин ограничены, например, числом С =1/4. Применяя теорему Чебышева (частный

Приняв во внимание, что математическое ожидание а каждой из величин Xi (т. е. математическое ожидание числа появлений события в одном испытании) равно ве-

Остается показать, что дробь (X1+X2+…Xn)/n равна относительной частоте т/п появлений события А в испытаниях. Действительно, каждая из величин X1,X2,…Xn при появлении события в соответствующем испытании принимает значение, равное единице; следовательно, сумма X1+X2+…+Xn равна числу m появления события в n испытаниях, а значит, ( X1 X 2 ... X n ) / n m / n. Учитывая, это равенство, окончательно получим

lim P(| m / n p | 1. Итак, теорема Бернулли утверждает, что при n

n

относительная частота стремится по вероятности к p.