
- •Преобразование Лапласа решетчатой функции
- •Анализ систем цифрового управления
- •Расчет компенсационных регуляторов методом логарифмических частотных характеристик (лчх)
- •1. Математическое описание цифровых систем
- •1.1. Расчетная схема цифровой системы. Аналого-цифровое и цифро-аналоговое преобразование
- •1.2. Математическое описание импульсного элемента
- •1.3. Преобразование Лапласа решетчатой функции
- •1.4. Передаточная функция экстраполятора
- •Пример.
- •Z‑преобразования некоторых числовых последовательностей.
- •Пример. Найдём z‑преобразование единичной ступенчатой функции.
- •Некоторые функции времени и их преобразования Лапласа и z‑преобразования
- •1.6. Передаточная функция непрерывной части цсу
- •1.7. Передаточная функция эвм
- •1.8. Частотные характеристики цифровых систем
- •1.9. Описание дискретных систем с помощью уравнений состояния
- •2. Анализ систем цифрового управления
- •2.1. Управляемость и наблюдаемость
- •2.2. Устойчивость цифровых систем
- •Пример 1.
- •Решение
- •2.3. Динамические показатели качества цифровых систем управления и их взаимосвязь с характеристиками непрерывных систем
- •2.4. Оценка точности цифровых систем
- •3. Синтез цифровых систем с заданными характеристиками
- •3.1. Повторный синтез. (Цифровое перепроектирование)
- •Перепроектирование по передаточным функциям системы.
- •Пример.
- •Перепроектирование по переходному процессу системы замкнутой по переменным состояния.
- •3.2. Расчет компенсационных регуляторов по дискретной модели
- •3.3. Расчет компенсационных регуляторов методом логарифмических частотных характеристик (лчх)
- •Определение алгоритма управления:
- •3.4. Расчет апериодических регуляторов (регуляторы с конечным временем установления)
- •Передаточная функция разомкнутой системы:
- •Отметим основные недостатки апериодических регуляторов:
- •3.5. Регуляторы состояния с заданным характеристическим уравнением
- •Пример.
- •3.6. Следящая система с заданным характеристическим уравнением
- •3.7. Регуляторы состояния при неполных измерениях. Наблюдатели состояния
- •3.8. Наблюдатели неполного порядка
- •3.9. Цифровое управление с учетом запаздывания
1.9. Описание дискретных систем с помощью уравнений состояния
Большинство современных методов проектирования систем управления основано на описании и моделировании систем в пространстве состояний. При изучении цифровых систем метод пространства состояний имеет следующие преимущества перед традиционным частотным методом:
Описание в пространстве состояний является естественным и удобным для решения задач на ЭВМ.
Позволяет унифицировать описание одномерных и многомерных систем.
Может применяться к некоторым типам нелинейных и нестационарных систем.
Однако достоинства хорошо известного частотного метода в его компактности и наглядности, физической интерпретируемости, и большое число задач проектирования реальных систем управления по-прежнему решается с использованием методов синтеза, основанных на определении передаточной функции.
Рассмотрим
непрерывный линейный объект, движение
которого описывается
координатами
![]() ,
имеющий
,
имеющий
![]() входных воздействий
входных воздействий
![]() (рис. 1.21).
(рис. 1.21).

В ведя
векторы:
ведя
векторы:
. .  ,
,
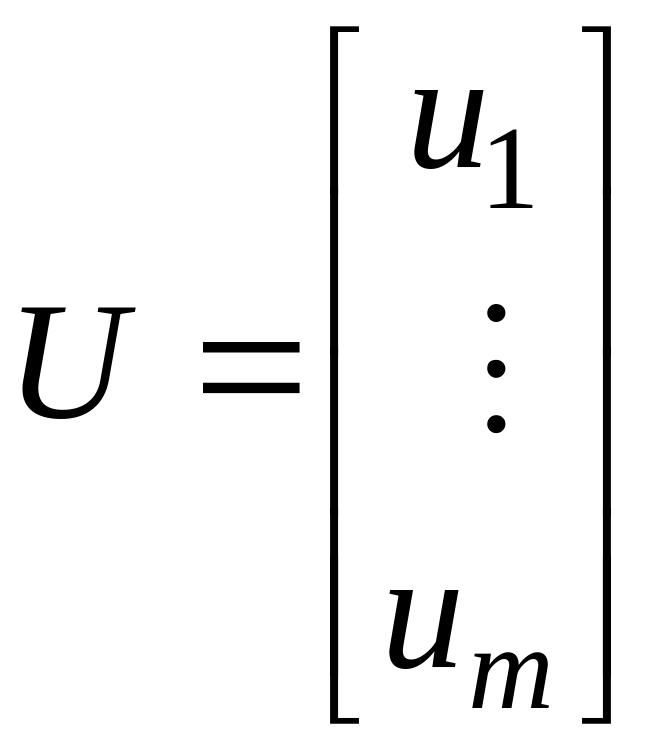 ,
,
получим стандартное описание линейного объекта в форме системы линейных дифференциальных уравнений 1-го порядка:
![]() ,
,
где
![]() и
и
![]() –
матрицы соответствующих размерностей.
Решение этой системы известно:
–
матрицы соответствующих размерностей.
Решение этой системы известно:
 ; (1.19)
; (1.19)
![]() –
начальное
состояние, переходная матрица состояния
–
начальное
состояние, переходная матрица состояния
![]() .
.

Пусть
теперь рассматриваемый объект имеет
дискретное управление (см. рис. 1.22).
Координаты
![]() будем рассматривать только в моменты
времени, совпадающие с моментами
замыкания ключа. Выберем произвольный
момент времени, соответствующий k-му
замыканию ключа, и будем считать его
начальным:
будем рассматривать только в моменты
времени, совпадающие с моментами
замыкания ключа. Выберем произвольный
момент времени, соответствующий k-му
замыканию ключа, и будем считать его
начальным:
![]() ;
;
![]() .
.
Следующий момент выборки будем считать текущим:
![]() .
.
![]() .
Тогда в соответствии с (1.19):
.
Тогда в соответствии с (1.19):
 . (1.20)
. (1.20)
Обозначим
![]() .
Очевидно,
что это постоянная матрица, если
постоянна, имеющая размерность
.
Очевидно,
что это постоянная матрица, если
постоянна, имеющая размерность
![]() .
Во втором слагаемом (1.20) выполним замену
переменных
.
Во втором слагаемом (1.20) выполним замену
переменных
![]() ,
тогда
,
тогда
![]() .
.
При
![]() :
:
![]() ,
при
,
при
![]() :
:
![]() .
.
Управление
![]() постоянно на интервале интегрирования
и потому может быть вынесено (вправо)
за знак интеграла. Тогда второе слагаемое
принимает вид:
постоянно на интервале интегрирования
и потому может быть вынесено (вправо)
за знак интеграла. Тогда второе слагаемое
принимает вид:
 .
.
Обозначим
 (
(![]() –
прямоугольная матрица той же размерности,
что
),
и получим:
–
прямоугольная матрица той же размерности,
что
),
и получим:
![]() .
.
Это уравнение состояния для дискретных объектов, которое позволяет по значению координат в текущий момент времени определить их значение в следующий дискретный момент времени.
Принята упрощенная запись:
![]() .
.
В
дальнейшем для упрощения записи будем
опускать в обозначениях матриц
и
индекс «![]() »
там, где это не может вызвать неоднозначное
толкование.
»
там, где это не может вызвать неоднозначное
толкование.
Как и в непрерывном случае, уравнение состояния дополняется алгебраическим уравнением выхода. Если выход скалярный, то это уравнение имеет вид:
![]()
Оно
не изменяется при переходе от непрерывной
к дискретной системе. В общем случае
![]() .
.
Решение уравнений состояния.
По
сути, уравнение состояния является
реккурентным соотношением. При
![]() начальное значение
начальное значение
![]() задано, воздействие
задано, воздействие
![]() тоже известно. Из уравнения состояния:
тоже известно. Из уравнения состояния:
![]() ;
;
![]() ;
и т. д.
;
и т. д.
Нетрудно получить общее выражение:
![]() .
.
Здесь
![]() –
общее решение
однородного разностного уравнения, а
–
общее решение
однородного разностного уравнения, а
![]() –
частное решение неоднородного разностного
уравнения.
–
частное решение неоднородного разностного
уравнения.
Можно
также получить решение уравнения
состояния, применив Z‑преобразование.
Пусть
![]() –
Z‑преобразование
решетчатой функции
–
Z‑преобразование
решетчатой функции
![]() ,
,
![]() .
По свойствам Z‑преобразования
.
По свойствам Z‑преобразования
![]() .
Тогда из уравнений состояния получим:
.
Тогда из уравнений состояния получим:
![]() ;
;
или
![]() ;
(
;
(![]() –
единичная матрица)
–
единичная матрица)
Решение:
![]() .
.
Найдем
изображение выхода, считая
![]() и полагая для простоты
и
и полагая для простоты
и
![]() скалярами:
скалярами:
![]() .
.
Нетрудно
видеть, что
![]() –
передаточная функция объекта и
–
передаточная функция объекта и
![]() .
.
Знаменателем
передаточной функции является
![]() (Так как
(Так как
![]() ),
а характеристическое уравнение объекта
),
а характеристическое уравнение объекта
![]() .
Его корни называют также собственными
числами матрицы
.
.
Его корни называют также собственными
числами матрицы
.
Если выход и/или управление не скаляры, мы получим матрицу передаточных функций от каждого входа к каждому выходу.
