
- •Преобразование Лапласа решетчатой функции
- •Анализ систем цифрового управления
- •Расчет компенсационных регуляторов методом логарифмических частотных характеристик (лчх)
- •1. Математическое описание цифровых систем
- •1.1. Расчетная схема цифровой системы. Аналого-цифровое и цифро-аналоговое преобразование
- •1.2. Математическое описание импульсного элемента
- •1.3. Преобразование Лапласа решетчатой функции
- •1.4. Передаточная функция экстраполятора
- •Пример.
- •Z‑преобразования некоторых числовых последовательностей.
- •Пример. Найдём z‑преобразование единичной ступенчатой функции.
- •Некоторые функции времени и их преобразования Лапласа и z‑преобразования
- •1.6. Передаточная функция непрерывной части цсу
- •1.7. Передаточная функция эвм
- •1.8. Частотные характеристики цифровых систем
- •1.9. Описание дискретных систем с помощью уравнений состояния
- •2. Анализ систем цифрового управления
- •2.1. Управляемость и наблюдаемость
- •2.2. Устойчивость цифровых систем
- •Пример 1.
- •Решение
- •2.3. Динамические показатели качества цифровых систем управления и их взаимосвязь с характеристиками непрерывных систем
- •2.4. Оценка точности цифровых систем
- •3. Синтез цифровых систем с заданными характеристиками
- •3.1. Повторный синтез. (Цифровое перепроектирование)
- •Перепроектирование по передаточным функциям системы.
- •Пример.
- •Перепроектирование по переходному процессу системы замкнутой по переменным состояния.
- •3.2. Расчет компенсационных регуляторов по дискретной модели
- •3.3. Расчет компенсационных регуляторов методом логарифмических частотных характеристик (лчх)
- •Определение алгоритма управления:
- •3.4. Расчет апериодических регуляторов (регуляторы с конечным временем установления)
- •Передаточная функция разомкнутой системы:
- •Отметим основные недостатки апериодических регуляторов:
- •3.5. Регуляторы состояния с заданным характеристическим уравнением
- •Пример.
- •3.6. Следящая система с заданным характеристическим уравнением
- •3.7. Регуляторы состояния при неполных измерениях. Наблюдатели состояния
- •3.8. Наблюдатели неполного порядка
- •3.9. Цифровое управление с учетом запаздывания
3.3. Расчет компенсационных регуляторов методом логарифмических частотных характеристик (лчх)
Рассматривается
одноконтурная следящая система
(см. рис. 3.5) с заданной передаточной
функцией объекта
![]() .
Для пояснения идеологии метода будем
условно считать, что известна дискретная
передаточная функция
,
хотя на самом деле первоначально задается
непрерывная функция
.
Для пояснения идеологии метода будем
условно считать, что известна дискретная
передаточная функция
,
хотя на самом деле первоначально задается
непрерывная функция
![]() ,
а дискретная может быть найдена только
после определения периода квантования
.
,
а дискретная может быть найдена только
после определения периода квантования
.

Метод
является графоаналитическим и использует
псевдочастотные характеристики, поэтому
от
надо перейти к частоте
![]() по формуле
по формуле
![]() .
В результате расчетов получаем
передаточную функцию регулятора
.
В результате расчетов получаем
передаточную функцию регулятора
![]() ,
а затем
,
по которой определяется алгоритм
управления.
,
а затем
,
по которой определяется алгоритм
управления.
По
идеологии метода компенсационных
регуляторов необходимо определить
желаемую передаточную функцию (![]() ).
В методе ЛЧХ используется желаемая
передаточная функция
).
В методе ЛЧХ используется желаемая
передаточная функция
![]() разомкнутой системы. Если она найдена,
то передаточную функцию регулятора
легко найти по формуле:
разомкнутой системы. Если она найдена,
то передаточную функцию регулятора
легко найти по формуле:
![]() .
.
Для построения желаемой передаточной функции задаются следующие исходные данные:
Требования к точности в установившихся режимах:
а) характеристики режима работы;
б )
допустимая ошибка
)
допустимая ошибка
![]() .
.
Требования к динамике:
а
)
требования к длительности
![]() переходного процесса:
переходного процесса:
![]() ;
;
б)
требования к перерегулированию
![]() :
:
![]() .
.
Характеристики
режима работы, как правило, четко не
определены. Обычно задаются максимальные
значения скорости и ускорения входного
сигнала
![]() и
и
![]() ,
а сам входной сигнал считается
синусоидальным (так называемая
эквивалентная синусоида):
,
а сам входной сигнал считается
синусоидальным (так называемая
эквивалентная синусоида):
![]() .
.
Амплитуду
![]() и частоту
и частоту
![]() эквивалентной синусоиды легко найти
из исходных данных. Дважды дифференцируя
входной сигнал, получаем:
эквивалентной синусоиды легко найти
из исходных данных. Дважды дифференцируя
входной сигнал, получаем:
![]() ;
; ![]() .
.
О тсюда
тсюда
![]() ;
;
![]() .
.
Амплитуда
ошибки
![]() при синусоидальном входном сигнале
определяется как:
при синусоидальном входном сигнале
определяется как:
![]() ;
; ![]() ; и
; и ![]() .
.
Поскольку амплитуда ошибки должна быть меньше заданной допустимой ошибки, отсюда находится требование к модулю желаемой передаточной функции на частоте эквивалентной синусоиды:
![]() .
.
Оно
определяет так называемую критическую
точку
![]() на логарифмической амплитудной
характеристике (ЛАХ).
на логарифмической амплитудной
характеристике (ЛАХ).
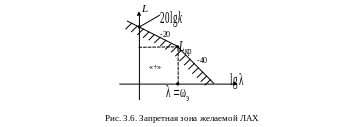
График ЛАХ, соответствующий (желаемой ЛАХ) должен быть выше . Для уточнения требований к желаемой ЛАХ на частотах в окрестности проведем следующие рассуждения.
Пусть
максимальная скорость
равна заданной, а максимальное ускорение
меньше указанного в задании. Строя новые
эквивалентные синусоиды и выполняя те
же преобразования, что и выше, можно для
разных значений
получить ряд новых точек
![]() .
Все эти точки находятся левее частоты
и ложатся на асимптоту с наклоном
–20 дБ/дек, проходящую через точку
(см. рис. 3.6).
.
Все эти точки находятся левее частоты
и ложатся на асимптоту с наклоном
–20 дБ/дек, проходящую через точку
(см. рис. 3.6).
Фиксируя теперь и уменьшая можно получить новый ряд критических точек, лежащих на асимптоте с наклоном –40 дБ/дек, проходящую через точку правее частоты . Две эти асимптоты образуют запретную область по точности, в которую не должна заходить желаемая ЛАХ.
Перейдем
к построению среднечастотного участка
желаемой ЛАХ, т.е. участка, прилегающего
к частоте среза. Он формируется исходя
из требований к динамике системы.
Оказывается, что требование
неудобно для использования в частотных
характеристиках, поэтому перерегулирование
преобразуют в
![]() –
показатель колебательности. График
такого преобразования можно найти
практически в любом учебнике по теории
управления.
–
показатель колебательности. График
такого преобразования можно найти
практически в любом учебнике по теории
управления.
Построение
начинается с определения частоты среза
![]() ,
которая находится на основании требований
к длительности переходного процесса
по формуле:
,
которая находится на основании требований
к длительности переходного процесса
по формуле:
![]() .
.
Множитель в числителе правой части выбирают тем большим, чем выше показатель колебательности.
Далее нужно выбрать период квантования из условия:
![]() ;
; ![]() .
.
Последнее требование должно выполняться с запасом в пять–десять раз во избежание потери устойчивости скорректированной системой.
Среднечастотный участок должен, как правило, иметь наклон –20 дБ/дек для обеспечения приемлемого качества переходного процесса. Границы среднечастотного участка определяются исходя из требований к показателю колебательности. Для левой границы среднечастотного участка должно выполняться следующее условие:
Сопрягающие частоты, меньшие частоты среза должны удовлетворять неравенству:
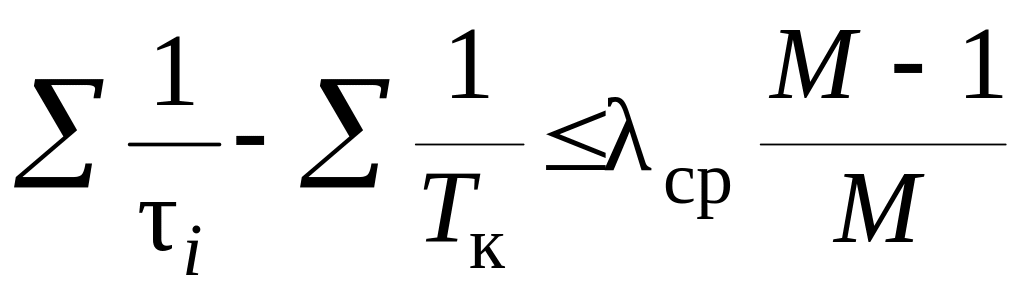 .
.
Для правой границы должно выполняться неравенство:
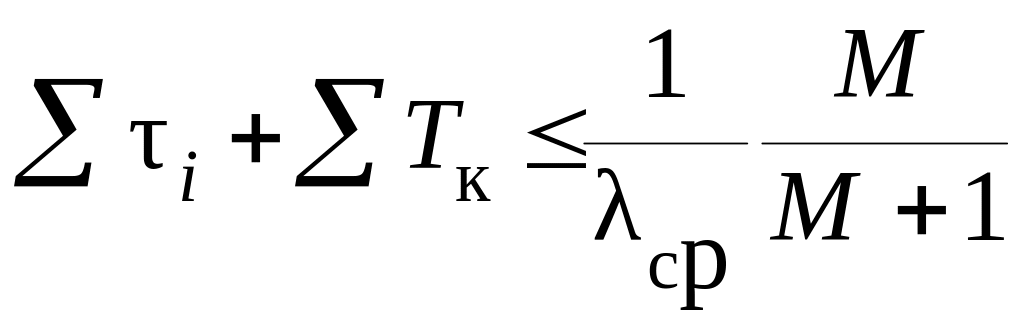 .
.
В
правой части этого неравенства суммируются
только те постоянные времени, которые
меньше чем
![]() .
.
Требование
к высокочастотной части желаемой ЛАХ
единственное: наклон её высокочастотной
асимптоты должен быть таким же, как
наклон высокочастотной асимптоты ЛАХ
объекта. Поскольку период квантования
определен, передаточная функция
![]() может (и должна) быть определена и её
ЛАХ построена. Кроме того, в желаемую
передаточную функцию необходимо включить
все неминимальнофазовые нули передаточной
функции объекта. Их отличительным
признаком является наличие знака «–»
в сомножителях числителя
.
может (и должна) быть определена и её
ЛАХ построена. Кроме того, в желаемую
передаточную функцию необходимо включить
все неминимальнофазовые нули передаточной
функции объекта. Их отличительным
признаком является наличие знака «–»
в сомножителях числителя
.
Можно заметить, что метод не дает жесткого алгоритма нахождения желаемой передаточной функции, а лишь определяет некоторые граничные требование к ней. Это оставляет разработчику значительную свободу выбора, но предъявляет повышенные требования к его квалификации.
Порядок синтеза в самом общем виде содержит следующие этапы:
Определение требований к желаемой передаточной функции, построение желаемой ЛАХ и определение
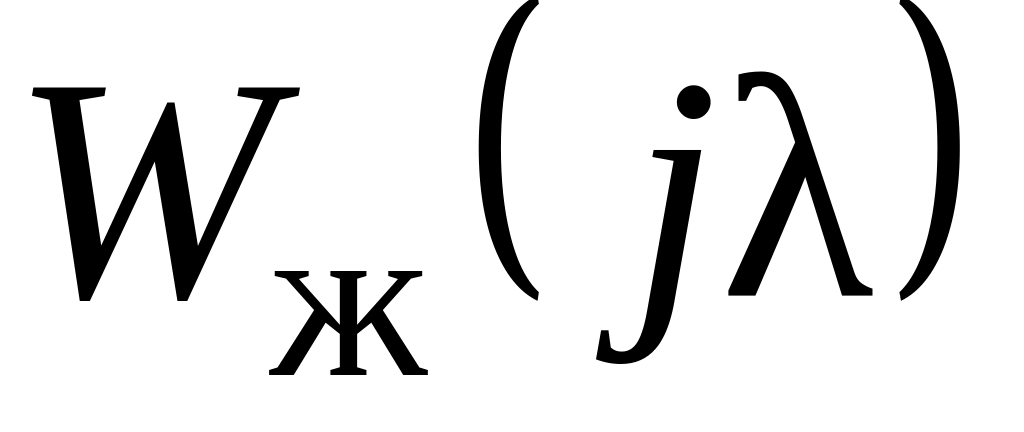 .
.Изменение коэффициент передачи объекта таким образом, чтобы ЛАХ объекта нигде не лежала ниже желаемой ЛАХ путем ввода дополнительного усиления в непрерывной части системы. Если этого не сделать, то ЦВМ придется выполнять функции усилителя. Новую передаточную функцию объекта обозначим
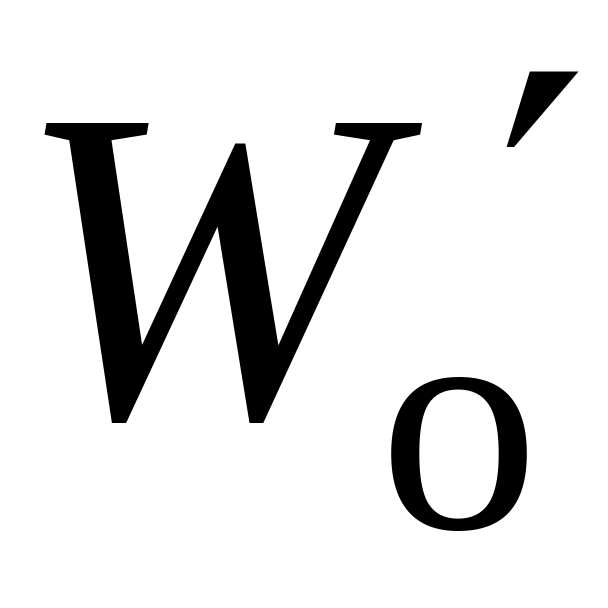 .
.Определение
 и переход к
,
либо определение
и
и переход к
,
либо определение
и
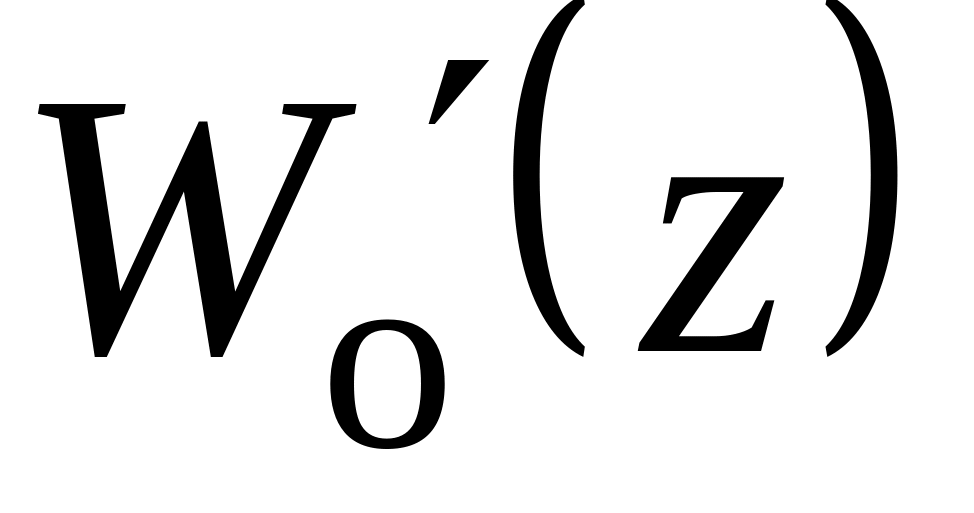 и затем получение
.
и затем получение
.Нахождение алгоритма управления по известному .
Пример.
Проектируется
следящая система для объекта с передаточной
функцией
![]() ;
;![]() ;
;
![]() ;
;
![]() .
.
Требования:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Построение желаемой ЛАХ:
Построение запретной области и низкочастотного участка.
![]() ;
; ![]() .
.
Частота эквивалентной синусоиды (абсцисса критической точки):
![]() .
.
Амплитуда синусоиды:
![]() .
.
Ордината критической точки:
![]() .
.
Построение среднечастотного участка.
Частота среза
;
примем
![]() .
.
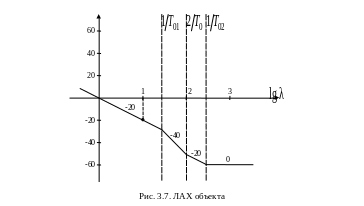
Вид низко- и среднечастотной части показан на рис. 3.7..
Левая граница среднечастотного участка
![]() .
.
![]() –
условие
выполняется.
–
условие
выполняется.
По
найденной частоте среза выбираем период
квантования
![]() .
.
Перед проверкой требований к правой границе найдем дискретную передаточную функцию объекта.
![]() .
.
![]() –
функция
имеет два неминимальнофазовых нуля.
–
функция
имеет два неминимальнофазовых нуля.
С учетом формы желаемой ЛАХ в низкочастотной части и наличия неминимальнофазовых нулей объекта запишем желаемую передаточную функцию в виде
![]() .
.
Сомножитель
![]() выравнивает порядки числителя и
знаменателя и обеспечивает нулевой
наклон высокочастотной асимптоты.
выравнивает порядки числителя и
знаменателя и обеспечивает нулевой
наклон высокочастотной асимптоты.
Для правой границы среднечастотного участка должно выполняться следующее условие: сумма всех малых постоянных времени, лежащих правее частоты среза, должна удовлетворять неравенству:
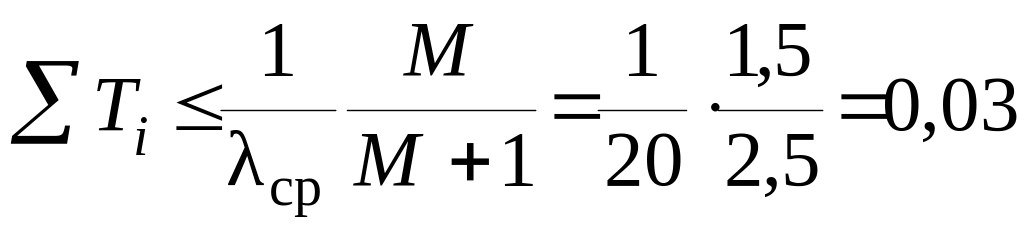 .
.
Отсюда
![]() и
и
![]() .
.
Возможные
варианты:
![]() или
или
![]() .
Выберем второе.
.
Выберем второе.
Окончательно:
![]() .
.
