1.3. Преобразование Лапласа решетчатой функции

Напомним, что общая формула преобразования Лапласа функции x(t) имеет вид:

Тогда преобразование Лапласа решетчатой функции

Здесь использовано селектирующее свойство δ‑функции. Окончательно

. (1.1)

Формулу (1.1) называют также дискретным преобразованием Лапласа.

Пусть  – преобразование Лапласа какой-то решетчатой функции. Введем понятие круговой частоты квантования:

.

Найдем , где  – любое натуральное число:

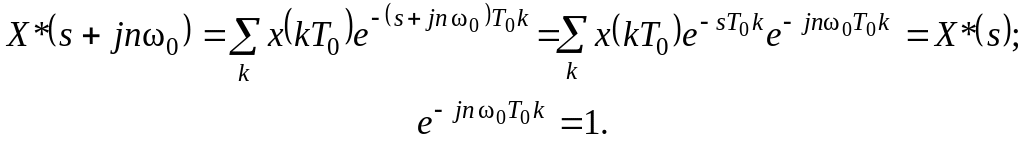
Следовательно, преобразование Лапласа решетчатой функции периодично по мнимой оси с периодом . Поэтому достаточно рассмотреть изменение комплексной переменной в одной полосе от до , в других полосах значения X*(s) будут повторяться по свойству периодичности.

Импульсная теорема.

Теоретическая возможность восстановления исходного сигнала по полученной в результате квантования импульсной последовательности определяется теоремой прерывания (теорема Котельникова-Шеннона, импульсная теорема).

Используя другой способ определения преобразования Лапласа решетчатой функции, можно доказать, что

. (1.2)

Эта формула важна тем, что дает связь между преобразованием Лапласа непрерывной функции и преобразованием Лапласа решетчатой функции , и в этом смысле может считаться неким аналогом передаточной функции импульсного элемента.

Перейдем к преобразованию Фурье:

;

.

Преобразование Фурье можно условно считать разложением непрерывных функций в синусоидальный ряд, аналогичный ряду Фурье при непрерывном изменении частоты.

Пусть  – амплитудный спектр функции . Это положительная четная функция, которая может иметь, например, вид, изображенный на рис. 1.9.

Пусть известен амплитудный спектр некоторого входного непрерывного сигнала. Попробуем определить амплитудный спектр соответствующего дискретного сигнала, воспользовавшись формулой (1.2):

. (1.3)

Понятно, что модуль суммы в общем случае не равен сумме модулей, т.е. спектр дискретного сигнала не равен в общем случае сумме смещенных спектров непрерывного сигнала. Предположим, что спектр непрерывного сигнала полностью укладывается в полосу – (кривая на рис. 1.10). Этот график представляет слагаемое суммы (1.3) при . При получим такой же график, но смещенный по оси частот вправо на величину . Аналогичная ситуация возникает при любых других .

Таким образом, спектр решетчатого дискретного сигнала при этих условиях представляет бесконечный ряд непересекающихся спектров непрерывного сигнала.

Выводом из этого факта является импульсная теорема (теорема Шеннона, теорема прерывания): если непрерывный сигнал не содержит частот выше , то он полностью описывается своими значениями, измеренными в дискретные моменты времени с интервалом .

Если условия теоремы выполняются, то на импульсном элементе не теряется никакой информации, если нет, то информация теряется, поскольку сдвинутые спектры непрерывного сигнала перекрываются и восстановить исходный по спектру дискретного сигнала невозможно.

1.4. Передаточная функция экстраполятора

В расчетной схеме цифровой системы экстраполятор моделирует ЦАП. Входом его считается решетчатая функция, принцип работы экстраполятора нулевого порядка иллюстрируется на рис. 1.11.

Для произвольноого k‑того момента времени ; где

 – амплитуда входного импульса.

Очевидно преобразование Лапласа .

Сигнал на выходе представляем как разность двух ступенчатых функций:

.

Таким образом, передаточная функция экстраполятора:

. (1.4)

1.5. Z-преобразование

Аппарат Z‑преобразования играет для цифровых систем ту же роль, что и преобразование Лапласа для непрерывных систем. Мотивировку его использования удобно пояснить на примере преобразования Лапласа квантованного сигнала. Пусть выходной сигнал идеального квантователя, как было показано, определен выражением:

(1.5)

Применяя преобразование Лапласа, получим:

(1.6)

Полученное выражение не является рациональной функцией относительно . Поэтому для построения формальной алгебры дискретных систем целесообразно преобразовать иррациональную функцию в рациональную, обозначаемую . Такое преобразование посредством замены комплексной переменной s на другую комплексную переменную z очевидно:

; (1.7)

(хотя и замена отвечает тем же требованиям). Из (1.7) следует .

Связь между и в (1.7) может быть определена как Z‑отображение. Подставляя (1.7) в (1.6), получим:

; (1.8)

что при представлении в комплексной форме является рациональной функцией относительно . Следовательно, можно определить как Z‑преобразование функции , т.е.:

;

где  – оператор Z‑преобразования.

Можно также записать:

.

Поскольку Z‑преобразование получается из преобразования Лапласа, то в общем случае для любой функции, имеющей преобразование Лапласа, существует также Z‑преобразование.

Отметим, что с формальной точки зрения не обязательно увязывать Z‑преобразование с преобразованием Лапласа. Достаточно просто определить Z‑изображение решетчатой функции формулой .

Процедура нахождения Z‑преобразования непрерывной функции включает следующие три этапа:

1. Определение как выходного сигнала идеального квантователя для входной функции .

2. Определение преобразования Лапласа

.

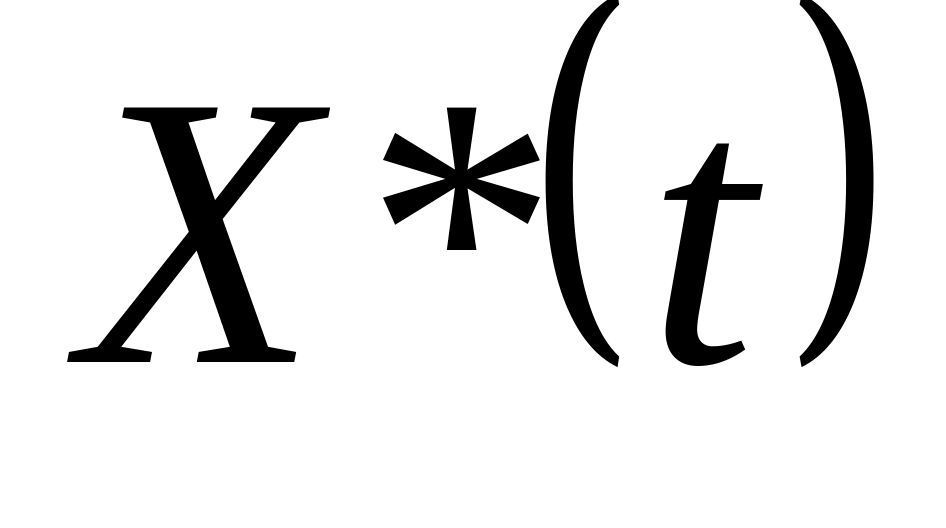
3. Замена 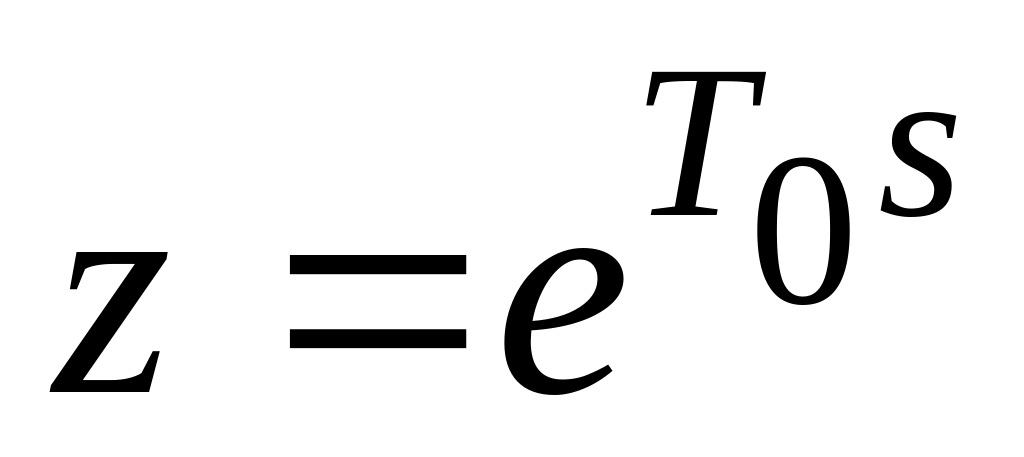в выражении , чтобы получить: