1.7. Передаточная функция эвм

На вход ЭВМ поступают сигналы с АЦП, которые мы рассматриваем как решетчатые функции времени. Для последовательного регулятора этот сигнал единственный, и пропорционален ошибке системы. Обозначим его (см. рис. 1.19). Выходной сигнал ЭВМ, подающийся на вход ЦАП, также условно считается решетчатым. Это сигнал управления .

В соответствии с принятыми допущениями ЭВМ может выполнять только линейные операции: сложение со знаком, умножение на константу и сдвиг во времени.

Тогда в самом общем виде алгоритм работы ЭВМ имеет форму:

Выполняя Z‑преобразование и вынося переменные, получим:

.

Отсюда:

.

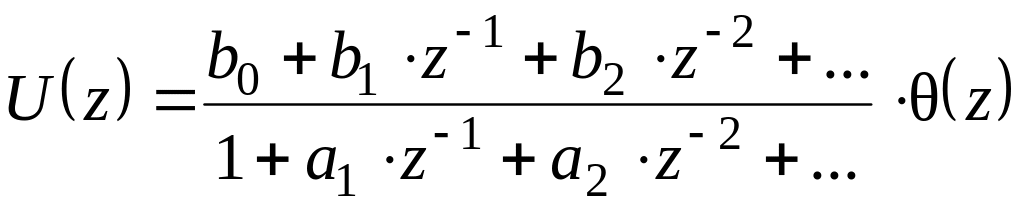Очевидно, что дробь в правой части и есть передаточная функция ЭВМ . Домножая числитель и знаменатель на в старшей степени, можно получить представление по положительным степеням . В таком представлении порядок числителя передаточной функции не может быть выше порядка знаменателя. В противном случае алгоритм не реализуем, так как от ЭВМ потребуется учитывать предсказанные значения входного сигнала.

Если алгоритм работы ЭВМ позиционный, т.е. в установившемся режиме постоянному входу соответствует постоянный выход, то для такого режима по передаточной функции можно найти коэффициент передачи ЭВМ. Для этого достаточно в положить .

Алгоритм работы ЭВМ может не быть позиционным и содержать действия, аналогичные интегрированию или дифференцированию. В первом случае передаточная функция будет содержать сомножители (один или более) вида , а во втором – вида .

1.8. Частотные характеристики цифровых систем

Рассмотрим сначала произвольный непрерывный линейный объект, (см. рис. 1. 20).

Стандартным образом перейдем к частотной передаточной функции, делая замену . Тогда . Эта передаточная функция имеет ясный физический смысл: если входной сигнал синусоидальный , то в установившемся режиме выход , амплитуда и фазовый сдвиг которого вычисляются с помощью функции по известным формулам: , .

Для дискретной системы . Здесь также можно сделать замену , переходя к частотной передаточной функции . Однако соотношения для амплитуды выхода и фазового сдвига при синусоидальном воздействии, справедливые для непрерывной системы, для дискретной системы выполняются с достаточной точностью только при . На высоких частотах выходной сигнал в общем случае не является синусоидой.

Можно доказать, что в силу периодичности частотную характеристику дискретной передаточной функции достаточно определить в пределах . Удобнее этот диапазон расширить до бесконечного с помощью замены независимой переменной , . Параметр называют относительной псевдочастотой. Видно, что прямая замена очень громоздка, поэтому применяется так называемое w-преобразование, при помощи которого окружность единичного радиуса отображается на мнимую ось плоскости комплексной величины . Для преобразования используется подстановка:

; (1.17)

или, соответственно:

. (1.18)

Переход осуществляется в очевидной последовательности .

Нетрудно показать:

.

Итого, псевдочастотная характеристика получается элементарной подстановкой

.

Для того, чтобы псевдочастота имела ту же размерность, что реальная, её масштабируют: . Параметр называют абсолютной псевдочастотой или просто псевдочастотой. Чтобы получить характеристику в функции абсолютной псевдочастоты нужно в передаточной функции сделать замену . Заметим, что при дробно-рациональной функция также дробно-рациональна. При имеем и . Следовательно, на низких частотах псевдочастота совпадает с реальной частотой. На этих частотах можно использовать приближенные формулы: , .

Пример.

Передаточная функция разомкнутой системы имеет вид: .

При подстановке получим .

Построение частотных характеристик даже в этом простейшем случае оказывается затруднительным.

Используем подстановку .

Тогда получим .

Построение частотных характеристик по последнему выражению не представляет трудностей.