
- •Преобразование Лапласа решетчатой функции
- •Анализ систем цифрового управления
- •Расчет компенсационных регуляторов методом логарифмических частотных характеристик (лчх)
- •1. Математическое описание цифровых систем
- •1.1. Расчетная схема цифровой системы. Аналого-цифровое и цифро-аналоговое преобразование
- •1.2. Математическое описание импульсного элемента
- •1.3. Преобразование Лапласа решетчатой функции
- •1.4. Передаточная функция экстраполятора
- •Пример.
- •Z‑преобразования некоторых числовых последовательностей.
- •Пример. Найдём z‑преобразование единичной ступенчатой функции.
- •Некоторые функции времени и их преобразования Лапласа и z‑преобразования
- •1.6. Передаточная функция непрерывной части цсу
- •1.7. Передаточная функция эвм
- •1.8. Частотные характеристики цифровых систем
- •1.9. Описание дискретных систем с помощью уравнений состояния
- •2. Анализ систем цифрового управления
- •2.1. Управляемость и наблюдаемость
- •2.2. Устойчивость цифровых систем
- •Пример 1.
- •Решение
- •2.3. Динамические показатели качества цифровых систем управления и их взаимосвязь с характеристиками непрерывных систем
- •2.4. Оценка точности цифровых систем
- •3. Синтез цифровых систем с заданными характеристиками
- •3.1. Повторный синтез. (Цифровое перепроектирование)
- •Перепроектирование по передаточным функциям системы.
- •Пример.
- •Перепроектирование по переходному процессу системы замкнутой по переменным состояния.
- •3.2. Расчет компенсационных регуляторов по дискретной модели
- •3.3. Расчет компенсационных регуляторов методом логарифмических частотных характеристик (лчх)
- •Определение алгоритма управления:
- •3.4. Расчет апериодических регуляторов (регуляторы с конечным временем установления)
- •Передаточная функция разомкнутой системы:
- •Отметим основные недостатки апериодических регуляторов:
- •3.5. Регуляторы состояния с заданным характеристическим уравнением
- •Пример.
- •3.6. Следящая система с заданным характеристическим уравнением
- •3.7. Регуляторы состояния при неполных измерениях. Наблюдатели состояния
- •3.8. Наблюдатели неполного порядка
- •3.9. Цифровое управление с учетом запаздывания
Пример 1.
Найти область допустимых значений коэффициентов для обеспечения асимптотической устойчивости системы с характеристическим уравнением:
![]() .
.

![]() ;
;
![]() ;
;
![]() .
.
Таким образом, имеем систему неравенств:
Для левого крайнего коэффициента четвертой строки:
![]() .
.
Для левого крайнего коэффициента шестой строки:
![]() .
.
Решение этих неравенств приводит к следующим соотношениям:
![]() ;
;
![]() ;
;
что
позволяет получить ограничения на выбор
допустимых значений
![]() ,
,
![]() (см. рис. 2.1).
(см. рис. 2.1).

Для
сравнения отметим, что система с
характеристическим уравнением
![]() устойчива при
устойчива при
![]() .
.
Оценка
устойчивости дискретных систем с помощью
критерия Рауса - Гурвица основана на
использовании билинейного преобразования
плоскости
![]() в плоскость
путём подстановки (1.17)
,
откуда
,
которая уже использовалась при построении
частотных характеристик. При этом
достигается взаимно однозначное
соответствие между областью действительных
чисел
в плоскость
путём подстановки (1.17)
,
откуда
,
которая уже использовалась при построении
частотных характеристик. При этом
достигается взаимно однозначное
соответствие между областью действительных
чисел
![]() для
и областью значений
для
и областью значений
![]() для
.
для
.
Представляя
полином
![]() и применяя к нему критерий Рауса-Гурвица,
получаем условия устойчивости дискретных
систем.
и применяя к нему критерий Рауса-Гурвица,
получаем условия устойчивости дискретных
систем.
Решение
.
При имеем:
![]() ,
,
откуда
![]() ;
;
![]()
Отметим, что подстановка (1.17) с последующим переходом к частотным характеристикам позволяет применять критерий устойчивости Найквиста
Пример 2.
Рассмотрим простейшую следящую систему (см. рис. 2.2), содержащую пару ВТ в трансформаторном режиме в качестве датчика рассогласования, усилитель и исполнительный двигатель постоянного тока.

Математическое описание, до предела упрощенное за счет пренебрежения инерцией объекта и электромагнитными процессами в якоре, может быть представлено структурной схемой (см. рис. 2.3).

![]()
Система
непрерывна. Передаточная функция
замкнутой системы
![]() ,
характеристическое уравнение
,
характеристическое уравнение
![]() или
или
![]() ,
его корень
,
его корень
![]() ,
следовательно при любом положительном
,
следовательно при любом положительном
![]() система устойчива.
система устойчива.
Сделаем из этой системы цифровую, введя цепочку АЦПЦВМЦАП. Положим при этом коэффициент передачи ЦВМ равным 1. Расчетная схема примет вид как на рис. 2.4.

По известной формуле:
![]() ;
где
;
где
![]() ;
по табл. 2
;
по табл. 2
![]() .
.
Окончательно:
![]() .
.
Передаточная функция замкнутой системы:
![]() .
.
Характеристическое
уравнение
![]() или
или
![]() ,
его единственный корень
,
его единственный корень
![]() . Условие
устойчивости
. Условие
устойчивости
![]() ,
отсюда
,
отсюда
![]() ;
;
![]() и
и
![]() .
.
Обратим
внимание на то, что в отличие от непрерывной
системы, цифровая система устойчива не
при любых положительных
,
а только при
![]() .
Это объясняется потерей информации при
квантовании сигнала по времени.
.
Это объясняется потерей информации при
квантовании сигнала по времени.
Рассчитаем переходный процесс:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
1 случай:
![]() После
подстановки и разложения в ряд Лорана
получаем:
После
подстановки и разложения в ряд Лорана
получаем:
![]()
2 случай:
![]() После
подстановки и разложения в ряд Лорана
получаем:
После
подстановки и разложения в ряд Лорана
получаем:
![]()
Графики переходных процессов показаны на рис. 2.5.

2.3. Динамические показатели качества цифровых систем управления и их взаимосвязь с характеристиками непрерывных систем
Динамические показатели качества дискретных систем определяются аналогично показателям систем непрерывного времени. Поскольку в основе дискретных моделей обычно лежат непрерывные процессы, целесообразно установить соотношения между динамическими показателями дискретных и непрерывных систем. Такие соотношения получаются на основе конформных отображений комплексных переменных.
Будем рассматривать дискретную систему вида (2.7), (2.8), полученную в результате дискретизации автономной непрерывной динамической системы, описываемой уравнениями состояния и выхода:
![]()
Характеристический
многочлен
![]() асимптотически устойчивой непрерывной
системы имеет полюсы:
асимптотически устойчивой непрерывной
системы имеет полюсы:
![]() ,
,
![]() ,
где
,
где
![]()
![]() .
.
Корни характеристических многочленов (полюсов) дискретной и непрерывной систем связаны выражением:
![]() ,
,
![]() . (2.13)
. (2.13)
В силу последнего выполняются следующие соотношения:
![]() ; (2.14)
; (2.14)
![]() ,
,
![]() ; (2.15)
; (2.15)
![]() ; (2.16)
; (2.16)
![]() . (2.17)
. (2.17)
Для
выбора интервала квантования
![]() при переходе к дискретной форме описания
на основе теоремы прерывания используется
условие
при переходе к дискретной форме описания
на основе теоремы прерывания используется
условие
![]() , (2.18)
, (2.18)
где
![]() ,
–
максимальная частота колебательных
составляющих переходных процессов
непрерывной системы.
,
–
максимальная частота колебательных
составляющих переходных процессов
непрерывной системы.
Поэтому в дальнейшем будем полагать, что для полюсов непрерывной системы выполняется
![]() . (2.19)
. (2.19)
Условие (2.19) отвечает, с одной стороны, требованиям теоремы прерывания, а с другой, в силу (2.17), вводит ограничение на аргументы полюсов дискретной системы.
Полюсы дискретной системы удовлетворяют условию
![]() ,
,
![]() ; (2.20)
; (2.20)
когда
полюсы
![]() непрерывной системы подчиняются условию
(2.19) комлекснозначная функция
непрерывной системы подчиняются условию
(2.19) комлекснозначная функция
![]() ; (2.21)
; (2.21)
определяет конформное отображение комплексных чисел и ставит в соответствие значениям полюсов непрерывной системы полюсы эквивалентной дискретной системы. При этом неравенства (2.19), (2.20) устанавливают области комплексной плоскости, в которых отображение (2.13) взаимно – однозначно. Это и служит формальным обоснованием возможности проведения анализа динамических показателей дискретных систем на основе известных свойств систем непрерывного времени.
Отметим основные свойства функции (2.21) (см. рис. 2.6):
Кусок левой полуплоскости, ограниченной прямыми
 ,
,
 ,
т.е. область
,
т.е. область
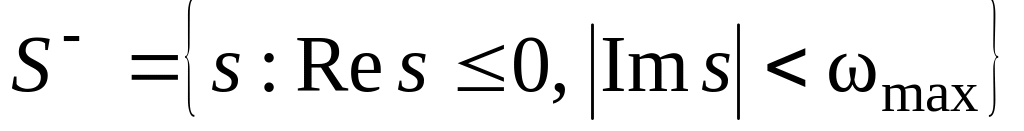 отображается в область
отображается в область
 т.е. в круг единичного радиуса, из
которого исключена левая вещественная
полуось.
т.е. в круг единичного радиуса, из
которого исключена левая вещественная
полуось.

Отрезок мнимой оси, ограниченной точками
 т.е.
т.е.
 отображается в кривую
отображается в кривую
 ,
т.е. в окружность единичного радиуса,
из которой исключена точка
,
т.е. в окружность единичного радиуса,
из которой исключена точка
 .
.Точка
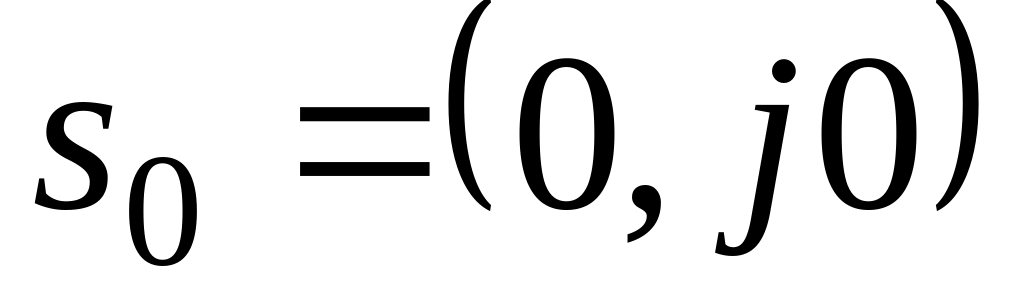 отображается в точку
отображается в точку
 .
.Бесконечно удалённая точка левой вещественной полуоси
 отображается в центр круга
отображается в центр круга
 ,
т.е. в точку
,
т.е. в точку
 .
.Граничные точки
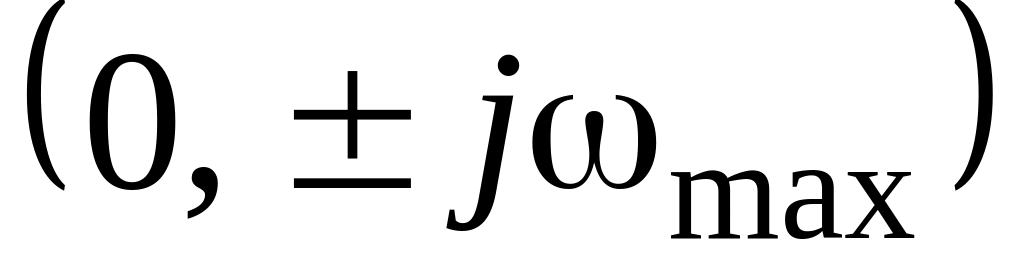 отрезка
отрезка
 отображаются в точку
отображаются в точку
 .
.
Перечисленные свойства сразу же позволяют сделать вывод об асимптотической устойчивости дискретной системы, полюсы которой лежат внутри единичной окружности.
Рассмотрим
оценку быстродействия. Значения модуля
полюсов системы
![]() уменьшаются с увеличением модулей
вещественных частей полюсов непрерывной
системы
уменьшаются с увеличением модулей
вещественных частей полюсов непрерывной
системы
![]() ,
что равносильно увеличению быстродействия.
Более того, в случае, когда дискретная
система имеет только нулевые полюсы
,
что равносильно увеличению быстродействия.
Более того, в случае, когда дискретная
система имеет только нулевые полюсы
![]()
![]() её переходный процесс заканчивается
не более чем за
шагов и, следовательно время переходного
процесса определяется выражением
её переходный процесс заканчивается
не более чем за
шагов и, следовательно время переходного
процесса определяется выражением
![]() . (2.22)
. (2.22)
Отмеченное обстоятельство служит основанием для введения (по аналогии с понятием степени устойчивости непрерывных систем) понятия степени устойчивости дискретной системы как радиуса распределения её полюсов на комплексной плоскости.
Степенью устойчивости дискретной системы называется положительное число
![]()
![]() . (2.23)
. (2.23)
Учитывая,
что скорость протекания процессов
возрастает при приближении полюсов к
началу координат
![]() можно заключить, что степень устойчивости
действительно характеризует быстродействие
дискретной системы, а при
можно заключить, что степень устойчивости
действительно характеризует быстродействие
дискретной системы, а при
![]() имеет место оценка (2.22).
имеет место оценка (2.22).
Для
установления связи степени устойчивости
со временем переходного процесса
воспользуемся свойствами отображения
(2.21) и
![]()
![]() т.е.
т.е.
![]() –
степень устойчивости такой системы.
–
степень устойчивости такой системы.
Грубая
оценка времени переходного процесса
даётся выражением
![]() .
.
Свойства
конформного отображения
![]() при
при
![]() и
и
![]() изображены на рис. 2.7:
изображены на рис. 2.7:
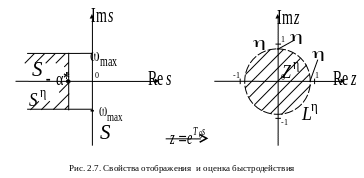
Учитывая,
что
![]() ,
откуда
,
откуда
![]() найдём грубую оценку времени переходных
процессов в цифровой системе:
найдём грубую оценку времени переходных
процессов в цифровой системе:
![]() . (2.24)
. (2.24)
Оценка
колебательности. Колебательность
непрерывных систем, как известно, связана
с наличием комплексно-сопряжённых
полюсов. Для устойчивой системы с
вещественными полюсами все составляющие
переходного процесса имеют апериодический
характер. При преобразовании
![]() левая вещественная полуось
левая вещественная полуось
![]() проецируется в единичный отрезок правой
вещественной полуоси:
проецируется в единичный отрезок правой
вещественной полуоси:
![]() .
.
Следовательно,
условием получения устойчивых
апериодических процессов дискретной
системы будет
![]() ,
,
![]() .
Для других значений полюсов из внутренности
единичного круга переходные процессы
носят колебательный характер. Показатель,
степень колебательности (или просто
колебательность) связан с размером
сектора
.
Для других значений полюсов из внутренности
единичного круга переходные процессы
носят колебательный характер. Показатель,
степень колебательности (или просто
колебательность) связан с размером
сектора
![]() ,
в котором расположены все полюсы системы
по формуле:
,
в котором расположены все полюсы системы
по формуле:
![]() ;
;
где
![]() ,
. (2.25)
,
. (2.25)
Рассмотрим
асимптотически устойчивую непрерывную
систему, полюсы которой удовлетворяют
условиям
и
![]() ,
т.е. расположены в секторе
,
(см. рис. 2.7).
,
т.е. расположены в секторе
,
(см. рис. 2.7).
Рис.
2.7. Свойства отображения
0
1
0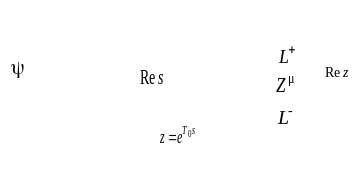
![]() и оценка колебательности
и оценка колебательности



![]()
![]()
![]()
![]()






![]()






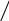
В
силу свойства сохранения углов область
расположения полюсов дискретной системы
![]() лежит в пределах сектора размера
лежит в пределах сектора размера
![]() .
Рассмотрим лучи
.
Рассмотрим лучи
![]() и
и
![]() сектора
сектора
![]() .
Их описание даётся выражением
.
Их описание даётся выражением
![]() ,
,
![]() ,
или в параметрической форме
,
или в параметрической форме
![]() ,
,
![]() .
.
Подставляя
последнее выражение в
,
получаем параметрическое описание
кривых
![]() ,
,
![]() на
комплексной плоскости дискретной
системы
на
комплексной плоскости дискретной
системы
![]() .
.
Найденные кривые и ограничивают область , в которой расположены полюсы дискретной системы, соответствующие заданной колебательности .
Если
учесть, что полюсы непрерывной системы
удовлетворяют условию
![]() ,
то параметр
,
то параметр
![]() .
.
Таким
образом, полюсы дискретной передаточной
функции удовлетворяют условиям
![]() ,
,
![]() ,
,
![]() ,
если полюсы системы удовлетворяют
условиям
,
,
если полюсы системы удовлетворяют
условиям
,
![]() .
.
