§6. Канонические уравнения прямой. Уравнения прямой, проходящей через две заданные точки

Из каждого уравнения в (19) выразим , полученные выражения приравняем и тогда будем иметь

. (20)

Эти соотношения называют каноническими уравнениями рассматриваемой прямой; здесь – заданные координаты точки прямой; – текущие координаты, т. е. координаты произвольной точки прямой; – заданные числа, равные проекциям на оси координат направляющего вектора прямой. Из формулы (20) можно получить уравнения

(21)

Ясно, что каждое из них, как уравнение первой степени относительно текущих координат в пространстве Oxyz, определяет плоскость. Пересекаясь, эти плоскости определяют рассматриваемую прямую. Соотношение (20) используется и в том случае, когда одно или два из чисел обращаются в нуль. Пусть, например, и , тогда имеем . В этом случае числители дробей, знаменатели которых равны нулю, мы также будем считать равными нулю, т. е. . Эти два уравнения определяют рассматриваемую прямую, причём каждое из них определяет плоскость, а прямая является линией их пересечения.

Уравнения прямой, проходящей через две заданные точки. Даны две точки , , лежащие на прямой. Координаты этих точек суть заданные числа. Нужно записать уравнения прямой, проходящей через эти две точки.

Вектор лежит на рассматриваемой прямой, поэтому его можно взять в качестве ее направляющего вектора. В качестве начальной точки прямой можно взять любую из указанных точек, например, . Тогда уравнения (20) запишутся так:

.

§7. Угол между двумя прямыми, условия параллельности и перпендикулярности

Пусть в пространстве Oxyz две прямые заданы уравнениями

, (22)

(23)

соответственно. Здесь – текущие координаты, остальные величины – заданные числа: – координаты точки на первой прямой; – координаты точки на второй прямой; – проекции на оси координат направляющего вектора прямой (22); – проекции на оси координат направляющего вектора прямой (23).

За угол между этими прямыми примем угол между их направляющими векторами и . Согласно формуле (18) главы 1 имеем

.

По найдем угол , измеряемый от до .

Если , то прямые (22), (23) параллельны, так как коллинеарны их направляющие векторы. Если , то прямые (22), (23) перпендикулярны, так как перпендикулярны их направляющие векторы.

§8. Уравнение линии на плоскости

Поступив так же, как в случае уравнения поверхности в пространстве, можно показать, что каждой линии на плоскости отвечает соотношение вида

, (24)

которому удовлетворяют координаты любой точки линии. Здесь – известное выражение, содержащее . Соотношение (24) называют уравнением линии на плоскости , где – текущие координаты. И, наоборот, уравнению вида (24) на плоскости отвечает некоторая линия – геометрическое место точек, координаты которых удовлетворяют (24), за исключением так называемых вырожденных случаев, когда уравнение ничего не определяет либо определяет лишь точку. Например, окружности радиуса с центром (рис. 20) отвечает уравнение

. (25)

В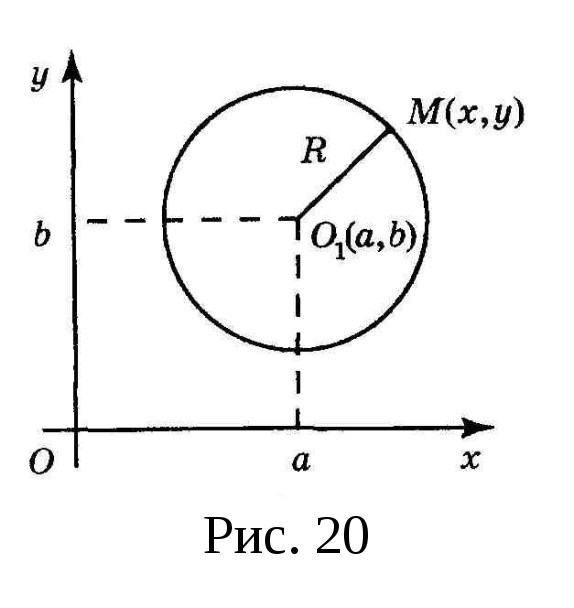 самом деле, для любой точки окружности расстояние . Возведя в квадрат это выражение, получим (25). Если совпадает с началом координат, то и , а (25) примет вид . Однако, например, уравнению отвечает лишь точка , а уравнению ничего не соответствует.