Глава 3. Элементы линейной алгебры
§1. Определители высших порядков
Определитель четвёртого порядка содержит 16 элементов и обозначается
.
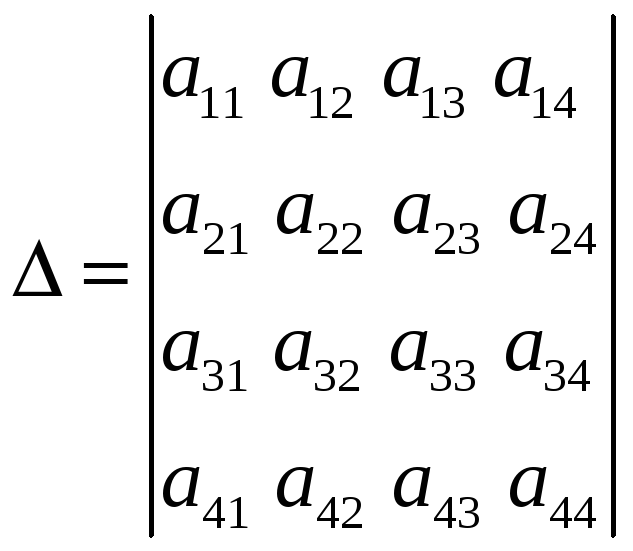Как и раньше,
элементы этого определителя обозначаются
,
где
– номер строки,
– номер столбца, которым принадлежит
элемент
,
,
.
Минором
для элемента
определителя
называется определитель третьего
порядка, получаемый вычёркиванием
строки и столбца, которым принадлежит
элемент
.
Зная этот минор, определим алгебраическое
дополнение
для элемента
определителя четвёртого порядка
.
(1)
Определителем четвёртого порядка называется число, определяемое формулой
(2)
Таким образом,
определитель четвёртого порядка
выражается через определители третьего
порядка. Аналогично, с помощью определителя
четвёртого порядка введём понятие
определителя пятого порядка, шестого
порядка и т. д. Зная определение
определителя (
)-го
порядка, введём понятие определителя
-го
порядка
(3)
Здесь
– алгебраические дополнения элементов
первой строки
.
Эти алгебраические дополнения по
формуле (1) выражаются через миноры
для соответствующих элементов первой
строки. Миноры – определители (
)-го
порядка. Таким образом, определитель
-го
порядка выражается по формуле (3) через
определители (
)-го
порядка. Соотношение (3) – разложение
определителя
-го
порядка по элементам первой строки.
Элементы
определителя образуют его главную
диагональ.
Можно показать (принимается без
доказательства), что определитель
раскладывается по элементам любой
строки или любого столбца. Например,
разложение определителя по элементам
-й
строки имеет вид
(4)
Разложение по
элементам
-го
столбца имеет вид
(5)
Таким образом, определитель равен сумме произведений элементов какого-либо ряда (строки или столбца) на их алгебраические дополнения.
§2. Свойства определителей
1. Определитель не изменится, если его столбцы сделать строками с теми же номерами (эта операция называется транспонированием):
.
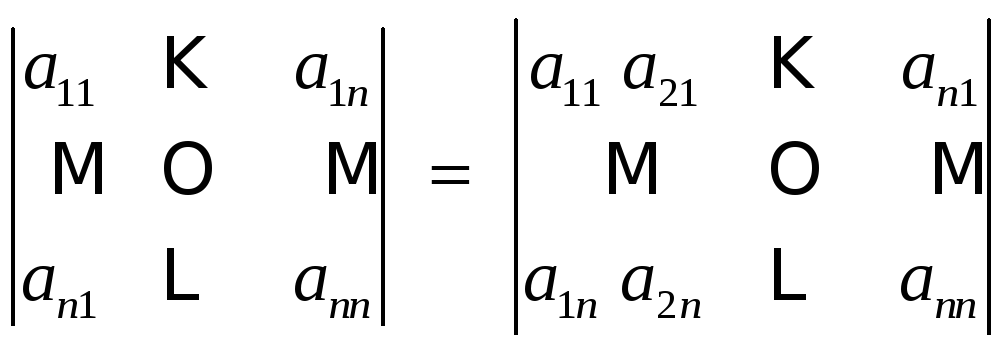Доказательство этого свойства опускаем (оно основано на (4) и (5)).
2. Определитель лишь изменит знак, если поменять местами два каких-либо ряда (две строки или два столбца). Например,
.
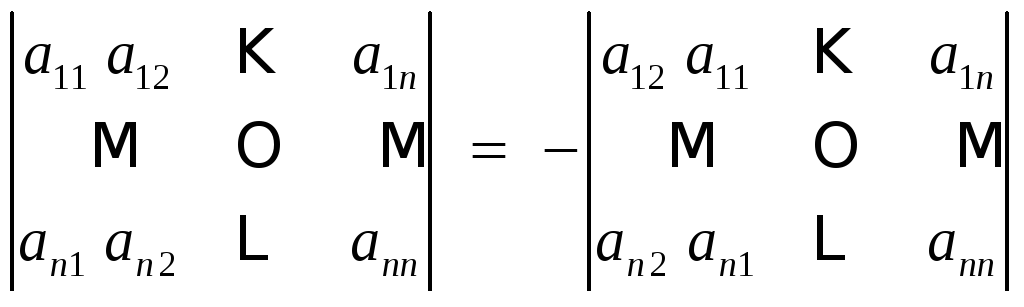В справедливости последнего равенства убедимся, разложив определители слева и справа по элементам соответственно первого и второго столбцов.
3. Определитель с двумя одинаковыми строками (столбцами) равен нулю.
Чтобы доказать это свойство, достаточно переставить одинаковые ряды и воспользоваться свойством 2.
4. Множитель, общий для элементов некоторого ряда определителя, можно вынести за знак определителя. Например, пусть – определённое число, тогда
.
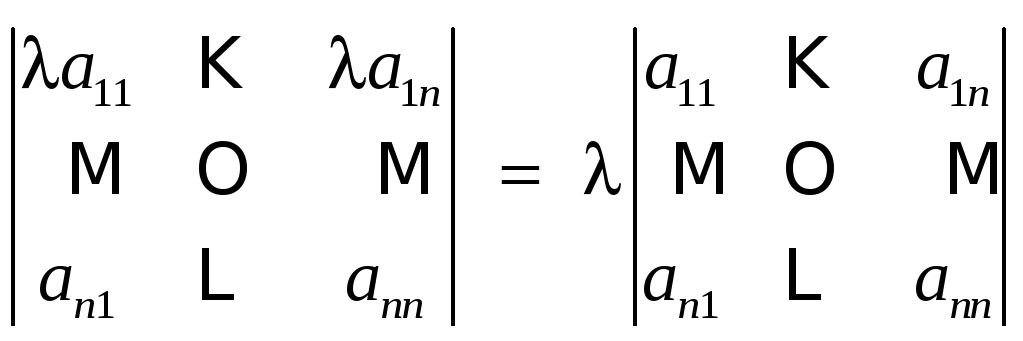Чтобы доказать это свойство, достаточно разложить определитель по элементам ряда, содержащим указанный множитель.
5. Если все элементы какой-либо строки (столбца) равны нулю, то и определитель равен нулю. Это свойство доказывается разложением определителя по нулевым элементам соответствующей строки (столбца).
6. Если к элементам некоторого ряда (строки или столбца) прибавить соответствующие элементы другого ряда, умноженные на одно и то же число, то определитель не изменится:
.
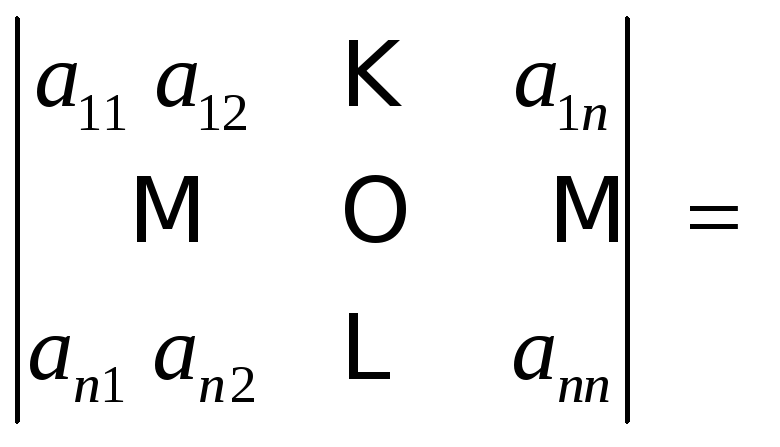
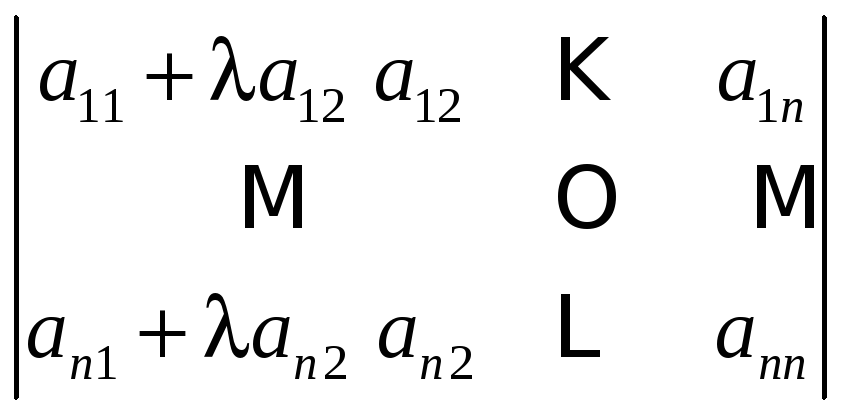Чтобы доказать это свойство, нужно разложить определитель в правой части по элементам первого столбца и учесть третье свойство.
7.
Сумма произведений элементов какого-либо
ряда определителя на алгебраические
дополнения соответствующих элементов
другого ряда равна нулю. Например,
.
Рассматриваемое свойство доказывается разложением определителя по элементам второго ряда с последующей заменой его элементов на соответствующие элементы первого ряда.
Приведенные выше свойства для определителей третьего порядка доказываются проверкой.