§6. Линейные операции над векторами, заданными своими проекциями

Пусть векторы и заданы своими проекциями: =(,,), Разложим векторы по формуле (6): Эти соотношения почленно сложим и учтём, что по свойству умножения вектора на число . Получим или

+=(+;+;+). (7)

Аналогично для разности

–=(–;–;–). (8)

Точно так же для произведения и

=(,,). (9)

Формула (7) показывает, что проекция на ось координат суммы векторов равна сумме проекций на эту ось слагаемых векторов. Подобное утверждение имеет место для формулы (8). Формула (9) показывает, что при умножении вектора на число на это число умножаются все проекции вектора.

§7. Длина вектора. Расстояние между двумя точками

Пусть вектор задан своими проекциями: =(,,). Перенесём его параллельно себе так, чтобы его начало совпало с началом координат. Получим =. Из рис. 9 видно, что

.

Согласно (5) аналогично и . Эти числа подставим в предыдущую формулу и получим . Извлечём квадратный корень и найдем длину вектора:

. (10)

Задача. Пусть в пространстве Oxyz точки и заданы координатами А и В (рис. 10). Нужно найти расстояние между ними.

Так как координаты точки равны проекциям на оси координат радиус-вектора этой точки, то и =. Согласно (8) =, но Значит, Отсюда видно, что проекции на оси координат вектора равны разностям соответствующих координат его конца и начала. Зная проекции , по формуле (10) найдём длину вектора , следовательно, и расстояние между точками и ||=

§8. Направляющие косинусы вектора

Пусть в пространстве Oxyz задан вектор =(,,). Поместим его начало в начало координат. Пусть – углы, образованные вектором с осями координат Ox, Oy, Oz (рис. 11). По формуле (3) для проекций этого вектора на оси координат имеем

(11)

В правые части вместо || подставим (10) и выразим косинусы углов:

(12)

Они называются направляющими косинусами вектора . Если все равенства в (12) возведём в квадрат и почленно сложим, то получим . Для единичного вектора, у которого ||=1, формулы (11) примут вид . Отсюда

§9. Скалярное произведение векторов, угол между

векторами. Условие ортогональности двух векторов

Даны два вектора и , начала которых расположены в одной точке, а угол между векторами равен . Такое расположение мы всегда можем получить, перенеся один из векторов параллельно.

Скалярное произведение двух векторов и обозначается (либо ) и определяется как число, равное произведению длин этих векторов на косинус угла между ними, т. е.

(,)=||||. (13)

Из определения ясно, что || = (проекция на ). С учётом этого соотношения формулу (13) запишем так:

(,) = || или (,) = ||. (14)

Скалярное произведение двух векторов равно произведению длины одного вектора и проекции другого вектора на направление первого. Угол между векторами и будем обозначать также .

Скалярное произведение обладает следующими свойствами:

• (,)=(,);

• (,)=(,)= (,), где – скалярный множитель;

• (,+)=(,)+(,).

Первое свойство показывает, что сомножители можно поменять местами; второе – что постоянный скалярный множитель можно вынести за знак скалярного произведения; третье – что при скалярном умножении векторов можно использовать правило умножения многочленов. Первые два свойства проверяются на основании определения скалярного произведения векторов, т. е. с помощью формулы (13). Докажем третье свойство.

С учётом (14) запишем

(,+ )=||=||+||=(,)+(,).

Пусть векторы заданы своими проекциями: поэтому =++, =++. Сначала для произведений базисных векторов , докажем справедливость соотношений

(,)=1; (,)=1; (,)=1; (15)

(,)=0; (,)=0; (,)=0; (16)

Действительно, по формуле (13) имеем ()=||||, поэтому (,)=1. Далее, (,)=||||=0. Остальные равенства в (15) и (16) доказываются аналогично.

Запишем скалярное произведение

(,)=(++, ++).

Использовав второе и третье свойства скалярного произведения, будем иметь

(,)=(,)+(,)+(,)+(,)+

+(,)+(,)+(,)+(

Отсюда с учётом (15) и (16) получим

(,)=++. (17)

Таким образом, скалярное произведение векторов равно сумме произведений одноименных проекций этих векторов.

Вычисление угла между векторами. Запишем || и || через проекции с использованием формулы (10). Из (13) следует, что . Следовательно, согласно (17)

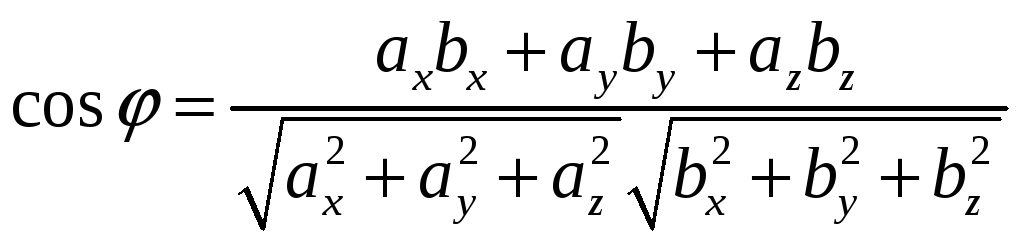. (18)

Зная найдем угол

Условие ортогональности (перпендикулярности) двух векторов. Если для ненулевых векторов и их скалярное произведение (,)=0, то вектор ортогонален вектору

В самом деле, пусть (,)=0, тогда согласно (13) имеем (,)=||||=0. Так как , , то =0. Значит, , т. е. векторы ортогональны.

Условие ортогональности двух векторов с учётом (17) можно записать следующим образом: ++=0.