
- •§1. Действительные числа, числовая ось, определители …
- •Глава 1. Элементы векторной алгебры
- •§1. Действительные числа, числовая ось, определители второго и третьего порядков
- •§2. Декартовы координаты. Полярные координаты
- •§3. Векторы, линейные операции над ними
- •§4. Проекция вектора на ось
- •§5. Разложение вектора по базисным векторам
- •§6. Линейные операции над векторами, заданными своими проекциями
- •§7. Длина вектора. Расстояние между двумя точками
- •§8. Направляющие косинусы вектора
- •§9. Скалярное произведение векторов, угол между
- •§10. Векторное произведение векторов, условие коллинеарности двух векторов, площадь треугольника
- •§11. Смешанное произведение векторов и его геометрический смысл. Условие компланарности трех векторов
- •Глава 2. Элементы аналитической геометрии
- •§1. Уравнение поверхности и уравнения линии в пространстве
- •§2. Плоскость, общее уравнение плоскости
- •§3. Угол между двумя плоскостями, условия параллельности и перпендикулярности плоскостей
- •§4. Расстояние от точки до плоскости в пространстве
- •§5. Прямая в пространстве и ее уравнения
- •§6. Канонические уравнения прямой. Уравнения прямой, проходящей через две заданные точки
- •§7. Угол между двумя прямыми, условия параллельности и перпендикулярности
- •§8. Уравнение линии на плоскости
- •§9. Общее уравнение прямой на плоскости, угол между прямыми
- •§10. Уравнение прямой с угловым коэффициентом,
- •§11. Уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом. Уравнение прямой, проходящей через две заданные точки
- •§12. Кривые второго порядка. Окружность
- •§13. Эллипс
- •§14. Гипербола
- •§15. Парабола
- •§16. Преобразование координат на плоскости
- •§17. Понятие о многомерном евклидовом пространстве
- •§18. Поверхности второго порядка. Сфера. Цилиндр
- •§19. Эллипсоид
- •§21. Однополостный и двуполостный гиперболоиды
- •§22. Эллиптический и гиперболический параболоиды
- •Глава 3. Элементы линейной алгебры
- •§1. Определители высших порядков
- •§2. Свойства определителей
- •§3. Матрицы и действия над ними. Обратная матрица
- •§4. Системы линейных алгебраических уравнений с неизвестными. Матричный метод решения
- •§5. Формулы Крамера
- •§6. Общая система линейных алгебраических уравнений. Метод Гаусса
- •§7. Ранг матрицы. Теорема Кронекера – Капелли
- •§8. Однородные системы
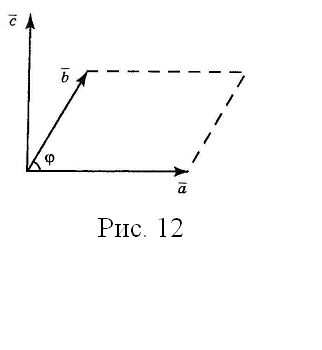
§10. Векторное произведение векторов, условие коллинеарности двух векторов, площадь треугольника
Даны два вектора
![]() и
и
![]() .
Построим их, поместив начала в общей
точке (см. рис. 12). Векторным
произведением двух векторов
.
Построим их, поместив начала в общей
точке (см. рис. 12). Векторным
произведением двух векторов
![]() и
и
![]() называется вектор (обозначаемый
называется вектор (обозначаемый
![]() ),
который обладает свойствами:
),
который обладает свойствами:
-
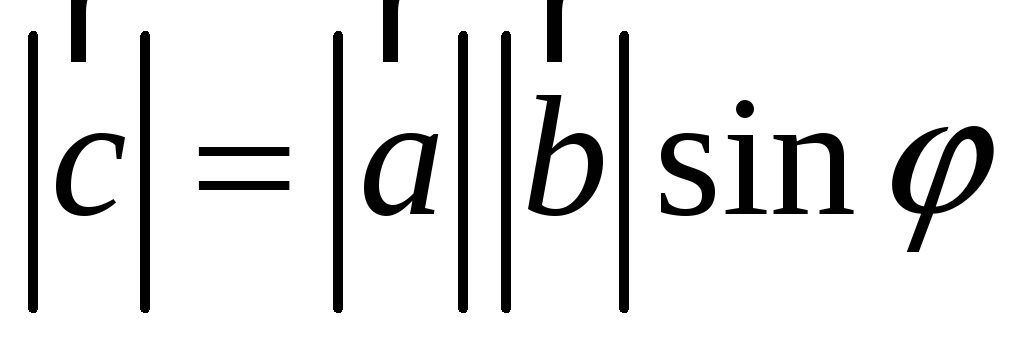 ,
т. е. длина вектора
,
т. е. длина вектора
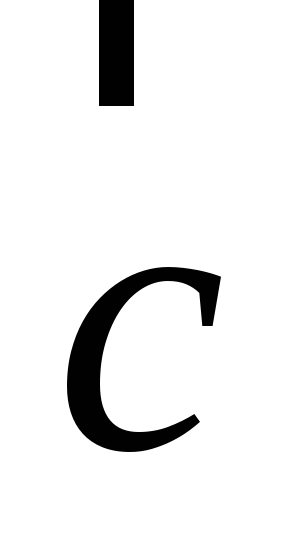 численно равна площади параллелограмма,
построенного на
численно равна площади параллелограмма,
построенного на
 ,
,
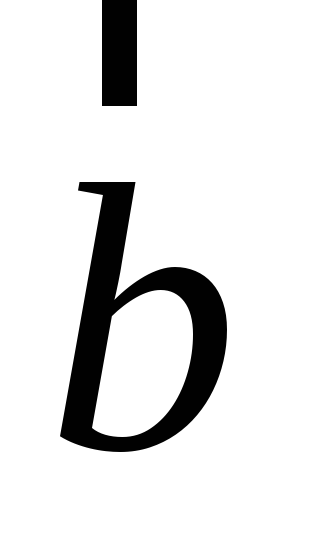 как на сторонах;
как на сторонах; -
 ,
,
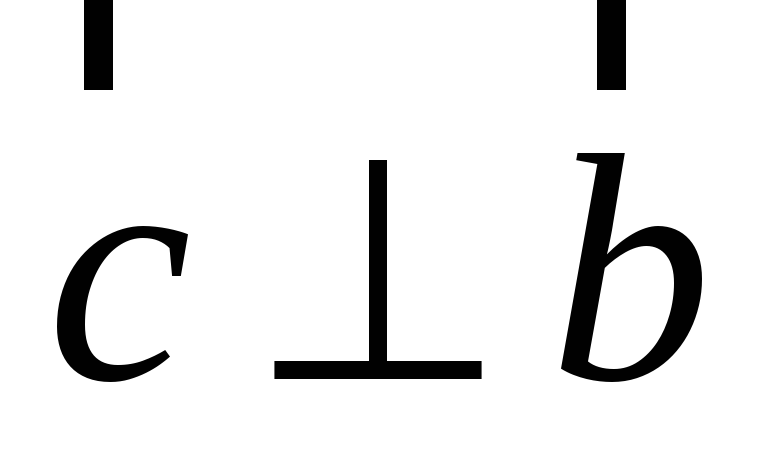 ,
т. е.
,
т. е.
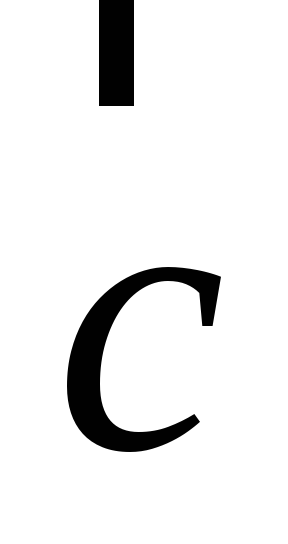 перпендикулярен к плоскости указанного
параллелограмма;
перпендикулярен к плоскости указанного
параллелограмма; -
вектор
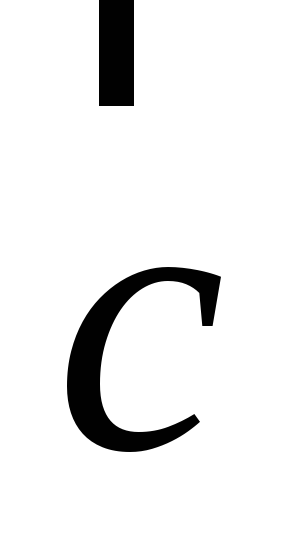 направлен так, что если смотреть с его
конца, то кратчайший поворот от первого
вектора
направлен так, что если смотреть с его
конца, то кратчайший поворот от первого
вектора
 ко второму вектору
ко второму вектору
 совершается против хода часовой
стрелки.
совершается против хода часовой
стрелки.
Для векторного
произведения
![]() применяют и другие обозначения:
применяют и другие обозначения:
![]() ,
,
![]()
![]() .
.
Векторное произведение обладает следующими свойствами:
![]()
![]()
![]()
Первые два свойства доказываются построением. Докажем справедливость равенства
![]()
Вначале отметим,
что любой вектор
![]() можно представить в виде
можно представить в виде
![]() где вектор
где вектор
![]() коллинеарен
коллинеарен
![]() а вектор
а вектор
![]() ортогонален
ортогонален
![]() (см. рис. 13). Чтобы в этом убедиться,
достаточно через начало вектора
(см. рис. 13). Чтобы в этом убедиться,
достаточно через начало вектора
![]() провести прямую, параллельную
провести прямую, параллельную
![]() через конец вектора
через конец вектора
![]() провести плоскость, перпендикулярную
провести плоскость, перпендикулярную
![]() точка их пересечения служит концом
точка их пересечения служит концом
![]() и началом
и началом
![]() (начало
(начало
![]() совпадает с началом
совпадает с началом
![]() ,
конец
,
конец
![]() – с концом
– с концом
![]() ).
).
З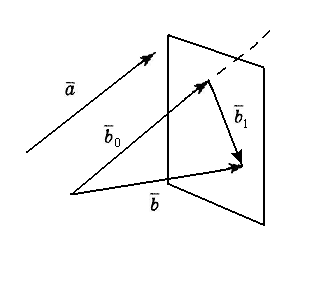 амечая,
что площадь параллелограмма, построенного
на векторах
амечая,
что площадь параллелограмма, построенного
на векторах
![]()
![]() равна площади параллелограмма,
построенного на векторах
равна площади параллелограмма,
построенного на векторах
![]()
![]() поскольку они имеют общую сторону
поскольку они имеют общую сторону
![]() ,
одну и ту же высоту
,
одну и ту же высоту
![]() ,
заключаем, что
,
заключаем, что
![]()
А
Рис. 13![]() где вектор
где вектор
![]() коллинеарен
коллинеарен
![]() а вектор
а вектор
![]() ортогонален
ортогонален
![]() будем иметь
будем иметь
![]()
Покажем, что
![]() или
или
![]()
где
![]() суть векторы, лежащие в одной плоскости,
так как они перпендикулярны
суть векторы, лежащие в одной плоскости,
так как они перпендикулярны
![]() Здесь имеем
Здесь имеем
![]()
поскольку вектор
![]() ортогонален и
ортогонален и
![]() и
и
![]() Кроме того,
Кроме того,
![]() Заметим, что
Заметим, что
![]() так как вектор
так как вектор
![]() ортогонален
ортогонален
![]() а вектор
а вектор
![]() ортогонален
ортогонален
![]() Но
Но
![]() ортогонален
ортогонален
![]() поэтому угол
поэтому угол
![]() равен углу между векторами
равен углу между векторами
![]() и
и
![]() Таким образом, векторы
Таким образом, векторы
![]() получаются поворотом вокруг
получаются поворотом вокруг
![]() соответственно векторов
соответственно векторов
![]()
![]()
![]() на угол, равный
на угол, равный
![]() в одном и том же направлении (против
хода часовой стрелки, если смотреть с
конца вектора
в одном и том же направлении (против
хода часовой стрелки, если смотреть с
конца вектора
![]() )
и умножением их на
)
и умножением их на
![]() .
Это означает, что
.
Это означает, что
![]() Учитывая, что
Учитывая, что
![]() где
где
![]() – вектор, коллинеарный
– вектор, коллинеарный
![]() ,
,
![]() ортогонален
ортогонален
![]() ,
и принимая во внимание предыдущие
соотношения, будем иметь
,
и принимая во внимание предыдущие
соотношения, будем иметь
![]() что
и требовалось.
что
и требовалось.
Пусть векторы
![]() и
и
![]() заданы своими проекциями:
заданы своими проекциями:
![]() =(
=(![]() ,
,![]() ,
,![]() ),
),
![]() .
Тогда
.
Тогда
![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() ,
,
![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() .
Сначала рассмотрим векторные произведения
базисных векторов.
.
Сначала рассмотрим векторные произведения
базисных векторов.
С помощью определения векторного произведения покажем справедливость равенств
[![]()
![]() ]=
]=![]() ;
[
;
[![]() ,
,![]() ]=
]=![]() ;
[
;
[![]() ,
,![]() ]=
]=![]() ;
[
;
[![]() ,
,![]() ]=
]=![]() ;
;
[![]() ,
,![]() ]=
]=![]() ;
[
;
[![]() ,
,![]() ]=
]=![]() ; (19)
; (19)
[![]() ,
,![]() ]=0;
[
]=0;
[![]() ,
,![]() ]=0;
[
]=0;
[![]() ,
,![]() ]=0. (20)
]=0. (20)
Итак, пусть [![]() ,
,![]() ]=
]=![]() .
Вектор
.
Вектор
![]() обладает свойствами:
обладает свойствами:
-
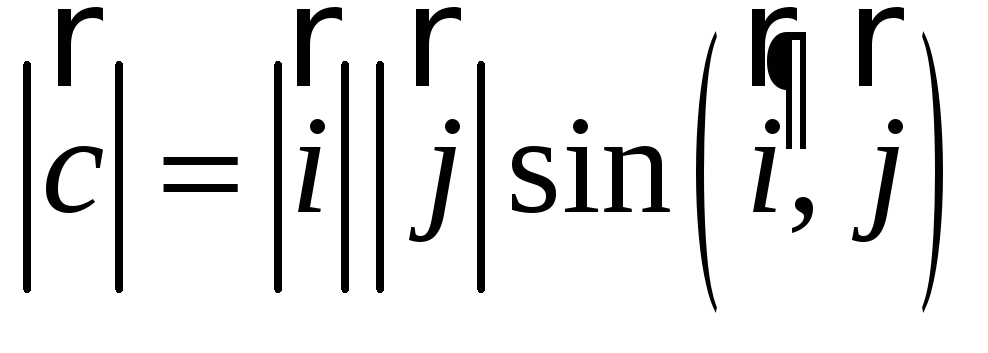 =
111
= 1;
=
111
= 1; -
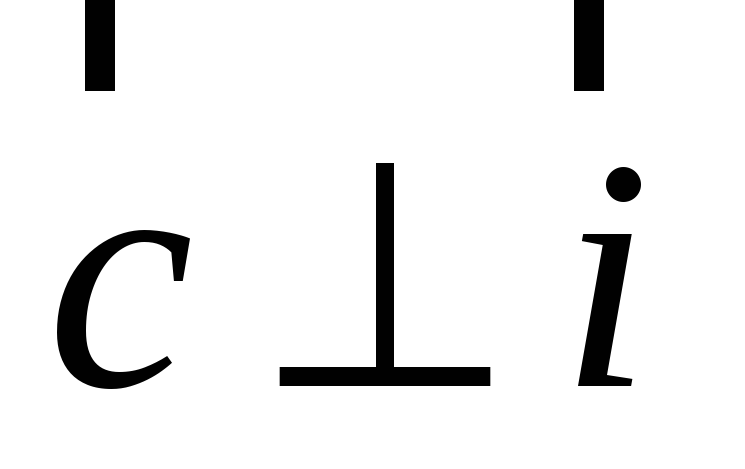 ,
,
 ,
т. е.
,
т. е.
 перпендикулярен к плоскости, в которой
лежат векторы
перпендикулярен к плоскости, в которой
лежат векторы
 и
и
 ;
; -
 направлен так,
что если смотреть с его конца, то
кратчайший поворот от первого вектора
направлен так,
что если смотреть с его конца, то
кратчайший поворот от первого вектора
 ко второму вектору
ко второму вектору
 совершается против хода часовой
стрелки, т. е.
совершается против хода часовой
стрелки, т. е.
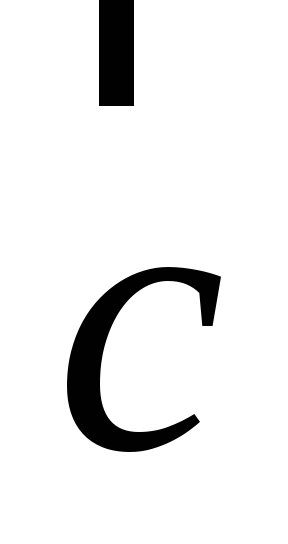 совпадает с
совпадает с
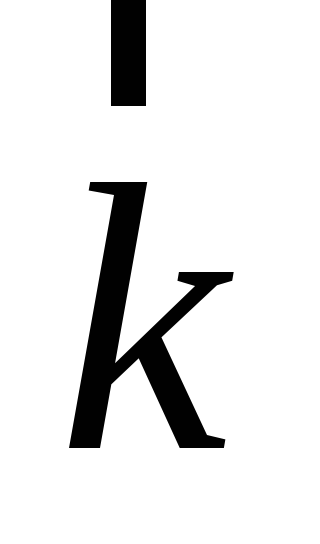 ,
следовательно, [
,
следовательно, [ ,
,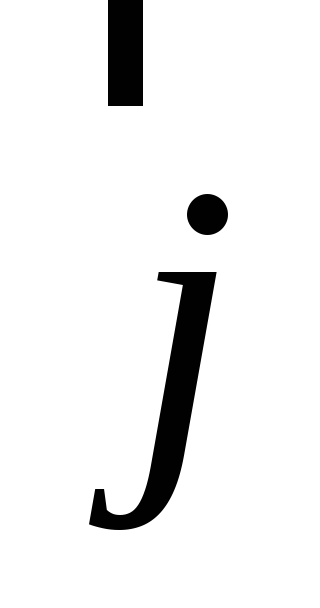 ]=
]=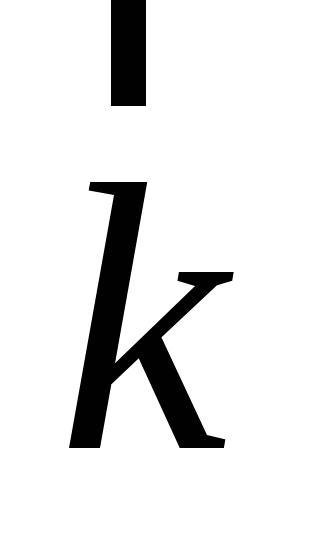 .
.
Покажем, что
[![]() ,
,![]() ]=0.
Пусть [
]=0.
Пусть [![]() ,
,![]() ]=
]=![]() .
Тогда
.
Тогда
![]() =0,
=0,
![]() =0,
т. е. [
=0,
т. е. [![]() ,
,![]() ]=0.
Аналогично доказываются остальные
равенства (19) – (20). Рассмотрим векторное
произведение [
]=0.
Аналогично доказываются остальные
равенства (19) – (20). Рассмотрим векторное
произведение [![]() ,
,![]() ]
= [
]
= [![]()
![]() +
+![]()
![]() +
+![]()
![]() ,
,
![]()
![]() +
+![]()
![]() +
+![]()
![]() ].
Использовав последние два свойства,
запишем
].
Использовав последние два свойства,
запишем
[![]() ,
,![]() ]=
]=![]()
![]() [
[![]() ,
,![]() ]+
]+![]()
![]() [
[![]() ,
,![]() ]+
]+![]()
![]() [
[![]() ,
,![]() ]+
]+![]()
![]() [
[![]() ,
,![]() ]+
]+
+![]()
![]() [
[![]() ,
,![]() ]+
]+![]()
![]() [
[![]() ,
,![]() ]+
]+![]()
![]() [
[![]() ,
,![]() ]+
]+![]()
![]() [
[![]() ,
,![]() ]+
]+![]()
![]() [
[![]() ,
,![]() ].
].
Отсюда с учётом (19) – (20) имеем
[![]() ,
,![]() ]=
]=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() +
+![]()
![]()
![]() +
+![]()
![]()
![]() -
-![]()
![]()
![]() .
.
Итак,
[![]() ,
,![]() ]=(
]=(![]()
![]() -
-![]()
![]() )
)![]() -(
-(![]()
![]() -
-![]()
![]() )
)![]() +(
+(![]()
![]() -
-![]()
![]() )
)![]() . (21)
. (21)
Следовательно (см. §1),
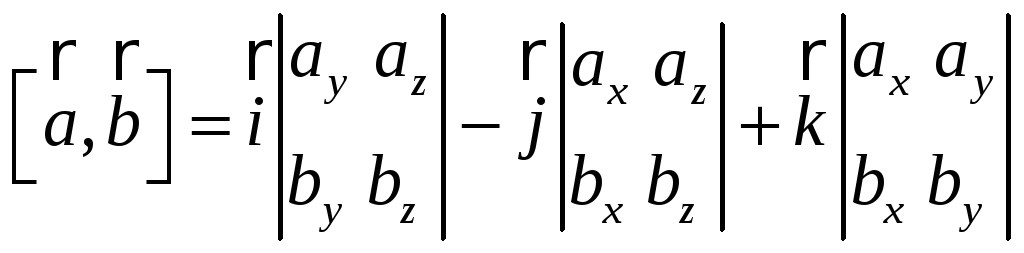 . (22)
. (22)
Эту формулу можно записать так:
 . (23)
. (23)
Таким образом,
если
![]() и
и
![]() заданы своими проекциями, то векторное
произведение двух векторов определяется
по формуле (23).
заданы своими проекциями, то векторное
произведение двух векторов определяется
по формуле (23).
Условие
коллинеарности двух векторов. Если
для ненулевых векторов выполняется
условие
![]() то
то
![]() и
и
![]() коллинеарны.
коллинеарны.
В самом деле, если
![]() то
то
![]() и
и
![]() ,
т. е.
,
т. е.
![]() или
или
![]() .
Следовательно, векторы
.
Следовательно, векторы
![]() ,
,
![]() коллинеарны.
коллинеарны.
В этом случае из
(21) имеем
![]()
![]() -
-![]()
![]() =0,
=0,
![]()
![]() -
-![]()
![]() =0,
=0,
![]()
![]() -
-![]()
![]() =0.
Значит,
=0.
Значит,
![]() Это и есть условие
коллине-арности двух векторов,
заданных своими проекциями.
Это и есть условие
коллине-арности двух векторов,
заданных своими проекциями.
Решим следующую задачу: определить площадь треугольника, заданного своими вершинами.
Пусть
![]() ,
,
![]() ,
,
![]() – вершины треугольника в пространстве
– вершины треугольника в пространстве
![]() ,
а их координаты – заданные числа. Найдем
векторы (см. §7)
,
а их координаты – заданные числа. Найдем
векторы (см. §7)
![]()
![]() векторное произведение которых обозначим
векторное произведение которых обозначим
![]() =
=
![]() Тогда согласно (22)
Тогда согласно (22)
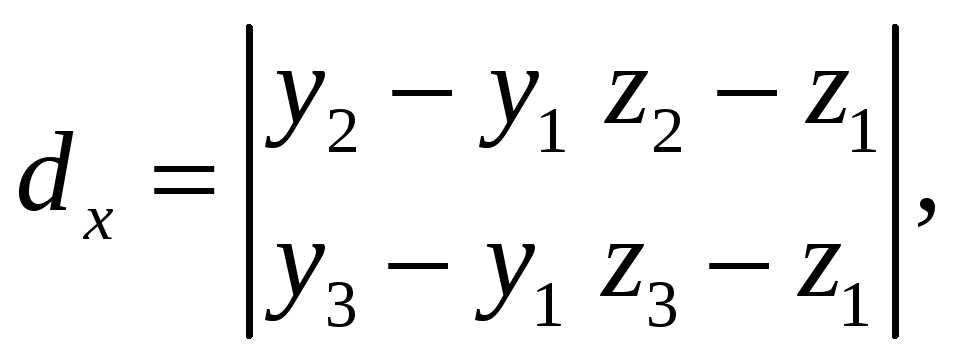
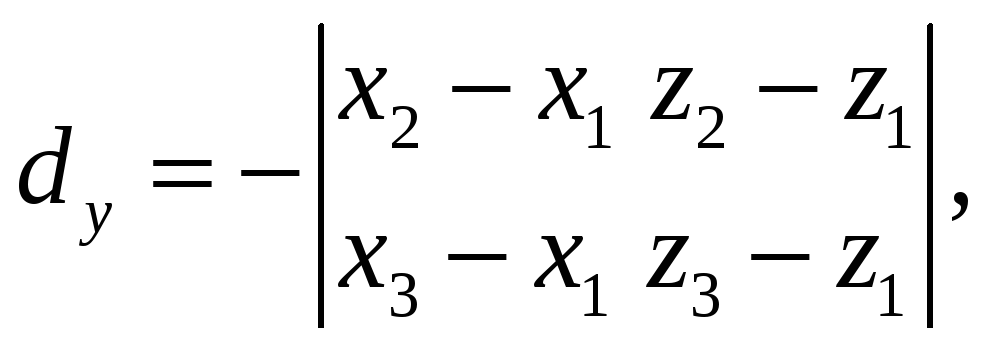

и
![]() Площадь параллелограмма, построенного
на векторах
Площадь параллелограмма, построенного
на векторах
![]() и
и
![]() равна найденному числу
равна найденному числу
![]() ,
поэтому искомая площадь треугольника
определяется по формуле
,
поэтому искомая площадь треугольника
определяется по формуле
![]() .
.
