
- •§1. Действительные числа, числовая ось, определители …
- •Глава 1. Элементы векторной алгебры
- •§1. Действительные числа, числовая ось, определители второго и третьего порядков
- •§2. Декартовы координаты. Полярные координаты
- •§3. Векторы, линейные операции над ними
- •§4. Проекция вектора на ось
- •§5. Разложение вектора по базисным векторам
- •§6. Линейные операции над векторами, заданными своими проекциями
- •§7. Длина вектора. Расстояние между двумя точками
- •§8. Направляющие косинусы вектора
- •§9. Скалярное произведение векторов, угол между
- •§10. Векторное произведение векторов, условие коллинеарности двух векторов, площадь треугольника
- •§11. Смешанное произведение векторов и его геометрический смысл. Условие компланарности трех векторов
- •Глава 2. Элементы аналитической геометрии
- •§1. Уравнение поверхности и уравнения линии в пространстве
- •§2. Плоскость, общее уравнение плоскости
- •§3. Угол между двумя плоскостями, условия параллельности и перпендикулярности плоскостей
- •§4. Расстояние от точки до плоскости в пространстве
- •§5. Прямая в пространстве и ее уравнения
- •§6. Канонические уравнения прямой. Уравнения прямой, проходящей через две заданные точки
- •§7. Угол между двумя прямыми, условия параллельности и перпендикулярности
- •§8. Уравнение линии на плоскости
- •§9. Общее уравнение прямой на плоскости, угол между прямыми
- •§10. Уравнение прямой с угловым коэффициентом,
- •§11. Уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом. Уравнение прямой, проходящей через две заданные точки
- •§12. Кривые второго порядка. Окружность
- •§13. Эллипс
- •§14. Гипербола
- •§15. Парабола
- •§16. Преобразование координат на плоскости
- •§17. Понятие о многомерном евклидовом пространстве
- •§18. Поверхности второго порядка. Сфера. Цилиндр
- •§19. Эллипсоид
- •§21. Однополостный и двуполостный гиперболоиды
- •§22. Эллиптический и гиперболический параболоиды
- •Глава 3. Элементы линейной алгебры
- •§1. Определители высших порядков
- •§2. Свойства определителей
- •§3. Матрицы и действия над ними. Обратная матрица
- •§4. Системы линейных алгебраических уравнений с неизвестными. Матричный метод решения
- •§5. Формулы Крамера
- •§6. Общая система линейных алгебраических уравнений. Метод Гаусса
- •§7. Ранг матрицы. Теорема Кронекера – Капелли
- •§8. Однородные системы
§14. Гипербола
Г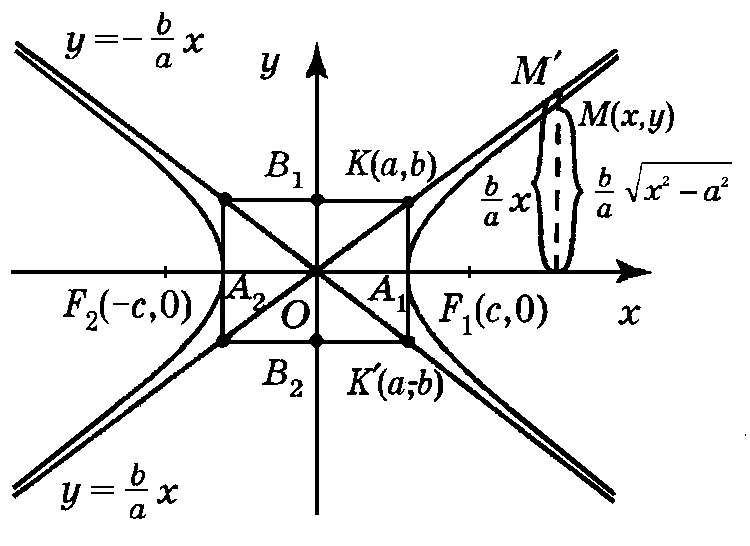 иперболой
называется геометрическое место точек
плоскости, разность расстояний которых
до двух данных точек, называемых
фокусами, есть величина постоянная
(рис. 25). Обозначим эту постоянную
иперболой
называется геометрическое место точек
плоскости, разность расстояний которых
до двух данных точек, называемых
фокусами, есть величина постоянная
(рис. 25). Обозначим эту постоянную
![]() ,
а фокусы – через
,
а фокусы – через
![]() и
и
![]() .
Расстояние между ними
.
Расстояние между ними
![]() .
Ось Ox
проведём через фокусы. Начало координат
О
возьмём в середине отрезка
.
Ось Ox
проведём через фокусы. Начало координат
О
возьмём в середине отрезка
![]() .
Тогда фокусы имеют координаты
.
Тогда фокусы имеют координаты
![]() ,
,
![]() .
Пусть
.
Пусть
![]() – произвольная точка гиперболы, тогда
по определению
– произвольная точка гиперболы, тогда
по определению
Рис. 25![]()
Знак «+» берётся,
когда левая часть положительна, а знак
«-» – когда левая часть отрицательна.
Расстояния
![]() и
и
![]() ,
как и раньше, выражаются формулами
(36). Подставим (36) в (39):
,
как и раньше, выражаются формулами
(36). Подставим (36) в (39):
![]() .
(40)
.
(40)
Получили уравнение
гиперболы. Как видно из рис. 25,
![]() есть длина стороны
есть длина стороны
![]() треугольника
треугольника
![]() ,
и она больше
,
и она больше
![]() ,
поэтому
,
поэтому
![]()
![]() – действительное число, которое будем
считать положительным. Уравнение (40)
упростим, убрав корни так же, как в
уравнении эллипса. Получим каноническое
уравнение гиперболы
– действительное число, которое будем
считать положительным. Уравнение (40)
упростим, убрав корни так же, как в
уравнении эллипса. Получим каноническое
уравнение гиперболы
![]() (41)
(41)
Исследуем форму
гиперболы, исходя из уравнения (41) (как
и в случае эллипса). Так как (41) содержит
![]() и
и
![]() только во второй степени, то Ox
и
Oy
являются осями симметрии гиперболы
(аналогично случаю эллипса), поэтому
точка пересечения этих осей – начало
координат
только во второй степени, то Ox
и
Oy
являются осями симметрии гиперболы
(аналогично случаю эллипса), поэтому
точка пересечения этих осей – начало
координат
![]() – центр симметрии гиперболы. Ясно, что
для установления вида гиперболы
достаточно рассмотреть картину в первой
четверти плоскости, где
– центр симметрии гиперболы. Ясно, что
для установления вида гиперболы
достаточно рассмотреть картину в первой
четверти плоскости, где
![]() и
и
![]() .
Для таких значений
.
Для таких значений
![]() ,
,
![]() из уравнения (41) выразим
из уравнения (41) выразим
![]() и получим
и получим
![]() .
(42)
.
(42)
Эта формула
выражает ординату
![]() точки
точки
![]() гиперболы, абсцисса которой есть
гиперболы, абсцисса которой есть
![]() .
При
.
При
![]() ордината
ордината
![]() ,
получим точку
,
получим точку
![]() гиперболы. С увеличением абсциссы точки
гиперболы. С увеличением абсциссы точки
![]() её ордината согласно (42) увеличивается.
Точка
её ордината согласно (42) увеличивается.
Точка
![]() уходит вправо, неограниченно поднимаясь
вверх. Остальные части гиперболы
строятся по симметрии.
уходит вправо, неограниченно поднимаясь
вверх. Остальные части гиперболы
строятся по симметрии.
Определим вид
гиперболы, когда
![]() неограниченно увеличивается. Возьмём
прямую с уравнением
неограниченно увеличивается. Возьмём
прямую с уравнением
![]() (43)
(43)
проходящую через
точки
![]() и
и
![]() Пусть
Пусть
![]() – точка прямой (43), имеющая ту же абсциссу
x,
что и точка M
гиперболы. Ординаты этих точек равны
– точка прямой (43), имеющая ту же абсциссу
x,
что и точка M
гиперболы. Ординаты этих точек равны
![]() и
и
![]() ,
так как координаты этих точек удовлетворяют
(43) и уравнению гиперболы (42). Разность
между указанными ординатами равна
расстоянию между точками
,
так как координаты этих точек удовлетворяют
(43) и уравнению гиперболы (42). Разность
между указанными ординатами равна
расстоянию между точками
![]() и
и
![]() ,
следовательно,
,
следовательно,
![]()
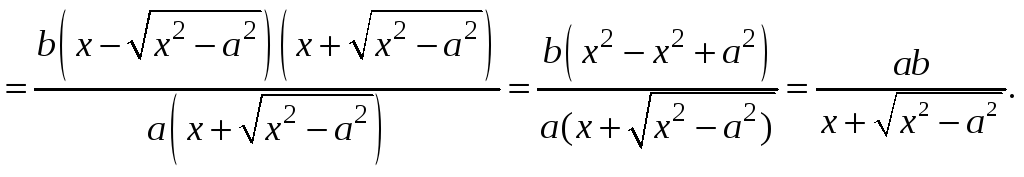 .
.
Для положительных
![]() знаменатель с увеличением
знаменатель с увеличением
![]() неограниченно увеличивается, поэтому
дробь убывает. Таким образом,
неограниченно увеличивается, поэтому
дробь убывает. Таким образом,
![]() стремится к нулю, т. е. точка
стремится к нулю, т. е. точка
![]() гиперболы приближается к точке
гиперболы приближается к точке
![]() прямой. В силу симметрии относительно
прямой. В силу симметрии относительно
![]() такая же картина будет в третьей четверти
плоскости.
такая же картина будет в третьей четверти
плоскости.
Возьмём теперь прямую
![]() .
(44)
.
(44)
Она симметрична
с прямой (43) относительно Ox,
проходит через точку
![]() и через точку
и через точку
![]() ,
симметричную с
,
симметричную с
![]() относительно Ox.
В силу симметрии гиперболы относительно
оси абсцисс
ясно, что гипербола по отношению к
прямой (44) расположена аналогично её
расположению к прямой (43). Прямые (43) и
(44) называются асимптотами.
относительно Ox.
В силу симметрии гиперболы относительно
оси абсцисс
ясно, что гипербола по отношению к
прямой (44) расположена аналогично её
расположению к прямой (43). Прямые (43) и
(44) называются асимптотами.
При построении
гиперболы целесообразно сначала
начертить ее асимптоты. Точки
![]() и
и
![]() пересечения гиперболы с осью Ox
называются
вершинами
гиперболы.
Расстояние между ними равно
пересечения гиперболы с осью Ox
называются
вершинами
гиперболы.
Расстояние между ними равно
![]() ,
,
![]() называется действительной
осью гиперболы;
называется действительной
осью гиперболы;
![]() и называется мнимой
осью.
и называется мнимой
осью.
