§11. Уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом. Уравнение прямой, проходящей через две заданные точки

Пусть дана точка , лежащая на прямой, и известен угловой коэффициент этой прямой. Нужно записать ее уравнение.

Так как эта прямая проходит через точку , то ее координаты удовлетворяют уравнению (30), т. е. . Полученное соотношение вычтем из (30) и придем к уравнению прямой, проходящей через точку :

. (31)

Пусть теперь даны две точки и . Нужно записать уравнение прямой, проходящей через них. Здесь можем воспользоваться уравнением (31). Величина пока не известна. Учтём, что прямая проходит также через точку , поэтому координаты этой точки должны удовлетворять уравнению (31), т. е. . Исключим из последних двух уравнений. Для этого нужно соотношение (31) почленно поделить на последнее. Получим искомое уравнение

§12. Кривые второго порядка. Окружность

Кривой второго порядка называется линия на плоскости определяемая уравнением второй степени относительно текущих координат , вида

. (32)

Здесь , , , , , – заданные числа, называемые коэффициентами уравнения. Cчитаем, что в этом уравнении коэффициенты , , одновременно не обращаются в нуль, поскольку в противном случае (32) обращается в уравнение первой степени.

Рассмотрим отдельные случаи уравнения (32) и соответствующие им кривые.

Окружность. Как мы уже знаем, окружность радиуса с центром в точке имеет уравнение

. (33)

В уравнении (33) в левой части раскроем скобки и получим

. (34)

В уравнении (34) коэффициенты при квадратах текущих координат равны друг другу. Кроме того, в этом уравнении отсутствует член, содержащий произведение текущих координат. Легко проверить, что если в уравнении (32) , , то оно будет определять окружность в плоскости (если уравнению отвечает множество точек). Чтобы убедиться в сказанном, достаточно уравнение (32) поделить на , после чего в левой части выделить полные квадраты членов, содержащих , и полные квадраты членов, содержащих . Таким образом перейдём к уравнению вида (33):

.

§13. Эллипс

Э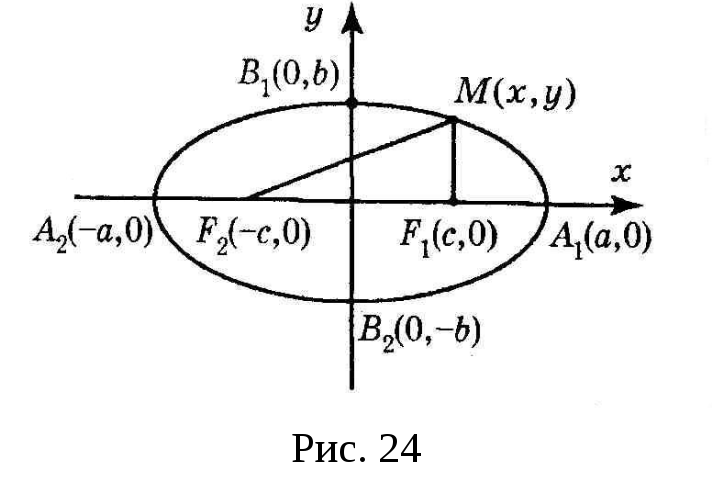ллипсом называется геометрическое место точек на плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная. Эту постоянную обозначим через , , а фокусы – через и . Расстояние между ними . Ось Ox проведём через фокусы. Начало координат О возьмём в середине отрезка, соединяющего фокусы. При указанном выборе осей координаты фокусов , . Пусть – произвольная точка эллипса, соединим ее с и (рис. 24). По определению эллипса сумма расстояний от любой точки эллипса до фокусов равна , т. е.

. (35)

Из треугольника видно, что . Запишем расстояния через координаты:

, . (36)

Эти выражения подставим в (35) и получим

.

Последнему соотношению удовлетворяют координаты любой точки эллипса, следовательно, это соотношение – уравнение эллипса. Нужно его упростить. Второй корень перенесём из левой части вправо и возведём обе части уравнения в квадрат. Тогда будем иметь

,

.

После приведения подобных членов в правой части оставим корень с множителем, остальные слагаемые перенесём влево и полученное выражение возведём в квадрат. Обозначим (так как ), считая После простых преобразований получим соотношение

. (37)

Такое уравнение эллипса называется каноническим. Имея уравнение (37), выясним форму эллипса.

Пусть – произвольная точка эллипса. На плоскости возьмём точку , имеющую ту же абсциссу , что и точка М, а ординату , отличающуюся от ординаты точки М только знаком. Точка симметрична относительно оси Ox. Уравнение (37) содержит только во второй степени и . Точка лежит на эллипсе, поэтому её координаты удовлетворяют уравнению эллипса, но тогда этому уравнению удовлетворяют координаты точки , так как абсцисса точки М равна абсциссе , а ординаты различаются лишь знаком. Получаем, что точка лежит на эллипсе, но сказанное относится к произвольной точке эллипса, следовательно, эллипс будет симметричным относительно оси Ox. Так как в (37) содержится только в квадрате, рассуждая аналогично, покажем, что ось Oy также является осью симметрии эллипса, следовательно, начало координат – центр симметрии эллипса. В силу симметрии форму эллипса достаточно выяснить для первой четверти плоскости для которой и . Для таких значений и уравнение (37) запишем так:

. (38)

Получили выражение для ординаты точки эллипса с абсциссой Когда абсцисса точки принимает значение , то согласно (38) ее ордината . Точка находится на Oy в точке. С увеличением абсциссы точки ордината этой точки согласно (38) уменьшается. Точка опускается и при ордината этой точки будет равна нулю, совпадет с точкой . Остальные части эллипса вычерчиваются по симметрии. Точки называются вершинами эллипса, а числа и – большой и малой осями эллипса соответственно (см. рис. 24).