§11. Смешанное произведение векторов и его геометрический смысл. Условие компланарности трех векторов

Даны векторы , и . Векторы , перемножим векторно и получим . Этот вектор умножим скалярно на и получим число , которое называется смешанным (векторно-скалярным) произведением трёх исходных векторов , , и обозначается

(, , ) = = . (24)

Рассмотрим это смешанное произведение, когда векторы заданы своими проекциями , , . Проекции вектора на оси координат определяются по формуле (22).

Скалярное произведение векторов и равно сумме произведений одноимённых проекций:

.

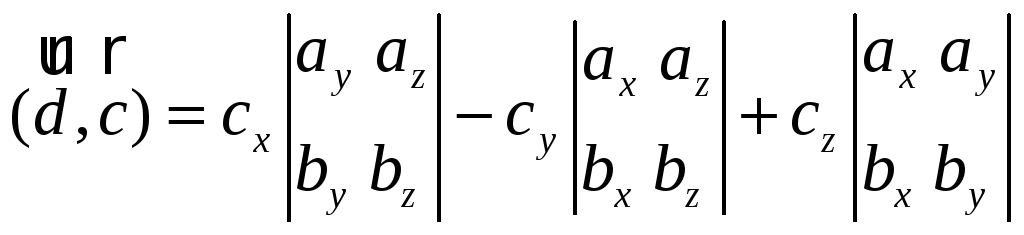Левая часть этой формулы – смешанное произведение (,,). Правую часть запишем в виде определителя третьего порядка:

. (25)

Эта формула позволяет вычислить смешанное произведение векторов, заданных своими проекциями. Выясним теперь

Геометрический смысл смешанного произведения. Даны векторы , и . Построим эти векторы, поместив их начала в общей точке, а затем на них как на рёбрах построим параллелепипед (рис. 14). Построим вектор , перпендикулярный к плоскости, в которой лежат векторы и , т. е. перпендикулярный к нижнему основанию параллелепипеда. Длина || равна площади нижнего основания параллелепипеда (т. е. площади параллелограмма, построенного на векторах и как на сторонах). Через конец проведём плоскость, перпендикулярную к (ясно, что верхнее основание параллелепипеда лежит в этой плоскости). Эта плоскость пересечёт вектор (или его продолжение) в точке К (К – проекция конца вектора на указанную линию). Из построения следует, что расстояние ОК равно высоте параллелепипеда. Пусть – угол между и . На рис. 14 изображен случай, когда при этом Смешанное произведение Но и Поэтому где – объём параллелепипеда. Этот результат мы получили для случая, когда . Если , то вектор лежит ниже плоскости векторов , , при этом и Итак, справедлива формула

(26)

где – объем параллелепипеда.

Определение. Три вектора называются компланарными, если они лежат в одной плоскости.

Условие компланарности трех векторов. Если для трёх ненулевых векторов , и выполняется условие

, (27)

то эти векторы компланарны.

Действительно, в этом случае согласно (26) имеем Отсюда следует, что три вектора лежат в одной плоскости, так как или или

Если , и заданы своими проекциями, то условие компланарности (27) с учётом (25) можно записать так:

.

Это условие проверяется непосредственно по заданным проекциям рассматриваемых векторов.

Глава 2. Элементы аналитической геометрии

§1. Уравнение поверхности и уравнения линии в пространстве

В аналитической геометрии любую поверхность в пространстве рассматривают как геометрическое место точек, обладающих определённым свойством. Расположим указанную поверхность в системе координат Oxyz. Свойство, общее для всех точек поверхности, запишем аналитически, т. е. в виде соотношения, связывающего координаты произвольной точки поверх-ности:

, (1)

где левая часть – известное выражение, содержащее . Формула (1) называется уравнением поверхности в пространстве Oxyz, а величины – текущими координатами. Например, сфера радиуса R с центром (0, 0, 0) (см. рис. 15) определяется уравнением

. (2)

В самом деле, для любой точки М() сферы расстояние ОМ=R. Заметив, что подставим это выражение в предыдущую формулу и перенесем влево, при этом получим (2). Поэтому (2) является уравнением сферы.

По построению уравнению (1) удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты точек, не лежащих на поверхности. Можно сформулировать и обратное утверждение: каждому уравнению вида (1) в пространстве Oxyz отвечает некоторая поверхность – геометрическое место точек, координаты которых удовлетворяют (1), если не имеет место случай, когда это уравнение не определяет никакого множества точек, например, , или когда уравнение определяет одну точку, например, .

Итак, каждой поверхности в пространстве Oxyz отвечает уравнение вида (1). Это обстоятельство позволяет свести изучение геометрических свойств поверхностей к изучению их уравнений аналитическими методами. Этим и занимается аналитическая геометрия.

Уравнения линии в пространстве. Линию в пространстве Oxyz будем рассматривать как линию пересечения двух поверхностей. Пусть каждая из этих поверхностей определяется одним из уравнений

(3)

Тогда координаты любой точки линии удовлетворяют каждому из этих уравнений, так как эта точка лежит на обеих поверхностях. Таким образом, линии отвечает система двух уравнений (3). Эта система называется уравнениями линии в пространстве.

Итак, линии в пространстве отвечает система уравнений (3) и, наоборот, каждой системе уравнений (3) в пространстве Oxyz отвечает некоторая линия – геометрическое место точек, координаты которых удовлетворяют этой системе.