
- •Моделирование химико-технологических процессов
- •Оглавление
- •Введение, основные понятия и определения
- •1. Методы моделирования и область их применения
- •1.1. Физическое моделирование (фм)
- •1.2. Математическое моделирование (мм)
- •2. Основные принципы и направления при построении и решении математических моделей
- •2.1. Составление математической модели
- •2.2. Нахождение решения математической модели
- •2.3. Проверка моделей на адекватность
- •3. Математическое описание структуры потока в аппарате – основа построения моделей
- •3.1. Методы исследования структуры потоков
- •3.2. Основные характеристики функции распределения потока по времени пребывания в аппарате
- •4. Типовые модели структуры потока
- •4.1. Модель идеального перемешивания
- •4.2. Модель идеального вытеснения
- •4.3. Ячеечная модель
- •4.4. Ячеечная модель с рециркуляцией
- •4.5. Диффузионная модель
- •4.6. Сравнение аппаратов соответствующих моделям ип и ив
- •5. Методы статистического анализа эксперимента
- •5.1. Основные характеристики случайных величин
- •5.2. Равномерное распределение
- •5.3. Нормальное распределение
- •5.4. Доверительные интервалы и доверительная вероятность, распределение Стьюдента
- •5.5. Определение общей дисперсии для серии параллельных опытов
- •5.6. Оценка дисперсии нормально распределенной случайной величины
- •5.7. Проверка однородности результатов измерений
- •6. Планирование эксперимента
- •6.1. Основные понятия и определения
- •6.2. Выбор области проведения эксперимента
- •6.3. Полный факторный эксперимент (пфэ)
- •6.4. Дробный факторный эксперимент
- •7. Оптимизация эксперимента
- •8. Планы второго порядка
- •8.1. Центральное композиционное планирование
- •8.2. Ортогональный план второго порядка
- •8.3. Ротатабельный план второго порядка
- •Список литературы
- •Приложение 1. Квантили нормального распределения
- •Приложение 2. Квантили распределения Пирсона
- •Приложение 3. Значения параметра для различных уровней значимости и степеней свободы
- •Приложение 4. Квантили распределения Стьюдента
- •Приложение 6. Пример использования модели ип для описания процесса непрерывной массовой кристаллизации
- •Приложение 7. Примеры использования типовых моделей для описания процесса теплообмена
- •Лицензия лр № 020370
2. Основные принципы и направления при построении и решении математических моделей
В ходе математического моделирования всегда приходится решать три основные задачи:
– составление модели;
– нахождение решения модели;
– проверку модели на адекватность.
Рассмотрим последовательно все три задачи.
2.1. Составление математической модели
Составление математических моделей осуществляют в соответствии с двумя взаимно перекликающимися аспектами: смысловым и аналитическим. Смысловой аспект представляет физическое описание объекта, аналитический – математическое описание объекта. Первичным, как правило, является физическое описание объекта. При этом выделяют протекающие в объекте «элементарные» процессы, формулируют основные допущения, принимаемые для их описания, и описывают. В данном случае под «элементарным» процессом понимают физико-химический процесс, относящийся к определенному классу явлений, например массообмен, теплопередача и т.п. Обычно при математическом моделировании принимают во внимание следующие «элементарные» процессы:
– движение потоков фаз;
– массообмен между фазами;
– теплопередачу;
– изменение агрегатного состояния;
– химические превращения и др.
Полнота рассмотрения «элементарных» процессов зависит от их роли, степени изученности и глубины взаимосвязи в общем процессе, а также желаемой точности описания. Взаимосвязь может быть очень сложной, поэтому на практике обычно делают различные упрощающие модель допущения. Например, при физическом описании процесса ректификации выделяют следующие «элементарные» процессы:
– гидродинамику потоков жидкости и пара в колонне;
– массообмен между жидкостью и паром;
– теплопередачу между жидкостью и паром;
– испарение жидкости и конденсацию пара.
Математическое описание объекта обычно начинают с математического описания «элементарных» процессов. Если есть необходимость, проводят эксперименты в условиях, максимально приближенных к условиям эксплуатации.
Как правило, сначала исследуют гидродинамическую модель процесса, являющуюся основой структуры математического описания всего объекта, затем кинетику химических реакций, процессы массо-, теплообмена и т.д. После этого с учетом гидродинамических условий составляют математические описания каждого из этих процессов. Заключительным этапом создания модели является объединение математических описаний «элементарных» процессов в единую систему уравнений математического описания всего объекта.
Составление математических моделей в зависимости от реальных условий может производиться различными методами: аналитическим (на основе данных полученных ранее), экспериментальным и экспериментально-аналитическим. Рассмотрим их последовательно.
Аналитический метод
Этот метод заключается в том, что вывод уравнений математического описания осуществляется на основании теоретического анализа физических и химических закономерностей протекания процесса, конструктивных параметров аппаратуры и свойств перерабатываемых веществ.
При выводе уравнений используются фундаментальные законы сохранения вещества и энергии, кинетические закономерности протекания химических процессов, процессов тепло-, массопереноса и других.
Аналитический метод используется для составления моделей только хорошо изученных процессов и не требует проведения экспериментов.
Недостатком этого метода является сложность решения полученных уравнений в случае сравнительно полного описания объекта.
Рассмотрим пример составления математического описания аналитическим методом. Пусть требуется получить математическую модель, описывающую закономерности движения частицы твердого материала в сепарационной зоне аппарата с кипящим слоем в зависимости от условий обтекания потоком.
Движение дисперсного материала в сепарационной зоне аппарата с кипящим слоем осуществляется в условиях восходящего потока газа, имеющего относительно низкую концентрацию твердой фазы. Для упрощения модели примем несколько допущений: взаимодействие между частицами материала отсутствует; частицы имеют шарообразную форму и движутся по прямолинейным траекториям; действующие на частицы силы, кроме сил тяжести и сопротивления, пренебрежимо малы; скорость потока во всех точках поперечного сечения аппарата равна средней скорости потока.
Выделим «элементарные» процессы. С
учетом принятых допущений таких процессов
два: гидродинамическое взаимодействие
частицы с восходящим потоком газа и
взаимодействие с гравитационным полем
земли. Проанализируем физические
закономерности подъема частицы в зоне
сепарации, скорость витания которой
больше скорости потока. В начальный
момент времени, вылетая из слоя под
гидродинамическим воздействием струй
газа, частица обладает скоростью
![]() и соответственно кинетической энергией
и соответственно кинетической энергией
![]() .
При движении частицы вверх, под действием
сил сопротивления
.
При движении частицы вверх, под действием
сил сопротивления
![]() и тяжести
и тяжести
![]() ,
скорость и кинетическая энергия частицы
уменьшаются и в точке максимального
подъема
,
скорость и кинетическая энергия частицы
уменьшаются и в точке максимального
подъема
![]() становятся
равными нулю:
становятся
равными нулю:
![]() и
и
![]() .
.
Рассмотрим элементарный участок пути
dH, на котором скорость
частицы изменится на величину
![]() ,
а кинетическая энергия на величину
,
а кинетическая энергия на величину
![]() ,
равную
,
равную
|
|
Изменение кинетической энергии произойдет в результате выполнения работы по преодолению сил сопротивления и тяжести,
|
|
где m, S – масса и площадь миделева сечения частицы соответственно.
|
|
здесь
![]() – коэффициент сопротивления частицы;
– коэффициент сопротивления частицы;
![]() –
текущая скорость частицы;
–
текущая скорость частицы;
![]() –
средний диаметр частицы;
–
средний диаметр частицы;
![]() – удельная плотность потока газа и
частицы соответственно; Wп
– средняя скорость потока газа; g –
ускорение силы тяжести.
– удельная плотность потока газа и
частицы соответственно; Wп
– средняя скорость потока газа; g –
ускорение силы тяжести.
Приравняв правые части уравнений (2.1) и (2.2), с учетом выражений (2.3), получим
|
|
Умножим и разделим дробь в квадратных
скобках на коэффициент сопротивления
частицы в условиях витания
![]() .
Тогда с учетом зависимости скорости
витания
.
Тогда с учетом зависимости скорости
витания
![]() от параметров процесса и частицы
от параметров процесса и частицы
|
|
получим
|
|
Уравнение (2.6) хорошо поясняет физическую
сущность процесса. Видно, что изменение
скорости частицы пропорционально
величине g, а также зависит от
соотношения сил сопротивления в текущих
условиях (числитель) и условиях витания
(знаменатель). Решим это уравнение для
условий ламинарного режима обтекания
частицы потоком газа. В этом случае
![]() и
и
![]() ,
где Re и Reв
значения критериев Рейнольдса
соответственно для текущих условий и
условий витания. Подставив значения
и
,
где Re и Reв
значения критериев Рейнольдса
соответственно для текущих условий и
условий витания. Подставив значения
и
![]() в уравнение (2.6), получим
в уравнение (2.6), получим
|
|
разделив переменные, будем иметь
|
|
Сделав несколько преобразований и выполнив подстановку
|
|
|
|
получим решение интеграла для случая Wк = 0
|
|
|
|
где
![]() .
.
Определив Wн и вычислив Wв с помощью хорошо известных из курса ПАХТ формул, по уравнению (2.12) можно легко найти максимальную высоту подъема частицы в условиях ламинарного режима.
Экспериментальный метод
Этот метод заключается в опытном определении функциональной зависимости между исходными параметрами и результатами процесса. Обычно такой подход используется для относительно узкого интервала изменения входных и выходных переменных. Достоинством экспериментальных методов является простота получения математического описания при достаточно точном описании свойств оригинала. К недостаткам относятся невозможность установления физической сущности процесса и невозможность распространения полученных эмпирических зависимостей на другие однотипные объекты.
Экспериментальные методы составления математического описания используются тогда, когда об объекте имеется мало теоретических сведений и основным источником данных является эксперимент, при этом экспериментатору доступен лишь контроль (иногда управление) над входными и выходными параметрами. В таких случаях говорят, что объект исследования является «черным ящиком». Другими словами, под «черным ящиком» подразумевают объект исследования, в котором для контроля доступны лишь входные и выходные параметры, а его внутренняя структура неизвестна (рис. 2.1.)


Рис. 2. 1. Принципиальная схема «черного ящика»
Входные параметры X называются факторами, в ходе проведения эксперимента они могут принимать различные значения, которые задаются исследователем либо устанавливаются пассивно. Значения, принимаемые факторами, называются уровнями их варьирования. Например, на приведенном ниже рисунке фактор X1 имеет 5 уровней варьирования.
Х1(1)
Х1(2)
Х1(3)
Х1(4)
Х1(5)![]()
Рис. 2.2. Уровни варьирования фактора X1
Выходные параметры Y называются параметрами оптимизации и зависят от факторов. В общем случае количество факторов не равно количеству параметров оптимизации.
Когда требуется изучить влияние одного фактора на параметры оптимизации, затруднений, как правило, не возникает ни с проведением опытов, ни с математической обработкой данных, полученных в результате эксперимента.
Например, требуется изучить влияние расхода теплоносителя на интенсивность теплопередачи и гидравлическое сопротивление теплообменника сложной формы (пластинчатый, спиральный и т.п.). В этом случае фактором будет расход теплоносителя G (тн/ч), уровнями – принимаемые значения данного фактора: 1, 2, ..., 10 , а параметрами оптимизации температура нагреваемого хладоагента Т (°С) и гидравлическое сопротивление аппарата Н (МПа).
В результате проведения эксперимента мы получим некоторые эмпирические зависимости параметров оптимизации от значений задаваемого фактора Y1 = f1(X) и Y2 = f2(X) (рис. 2.3). Уравнения, описывающие эти зависимости, будут называться функциями отклика объекта на задаваемое возмущение.

Рис. 2.3. Зависимость параметров оптимизации от задаваемых значений факторов
Намного сложнее получить функцию отклика и провести эксперимент, когда требуется изучить влияние на процесс нескольких факторов одновременно. Так как, во-первых, резко возрастает количество опытов, равное N = nk, где k – количество задаваемых факторов, а n – количество принимаемых ими уровней. Например, при исследовании процесса пневмоклассификации обычно требуется изучить влияние, как минимум, четырех факторов: скорость газа; расход материала; скорость витания и какой-нибудь конструктивный параметр аппарата. Тогда, если мы хотим исследовать каждый фактор на 5 уровнях, т.е. при 5 различных значениях, то количество опытов будет равно N = 54 = 625, что не всегда реально. Во-вторых, возрастает сложность математической обработки полученных многофакторных зависимостей. Поэтому, когда факторов несколько, эксперимент проводят на основе законов математической статистики и называют статистическим экспериментом. При наличии необходимой информации о факторах и параметрах оптимизации, законы статистики позволяют построить математическую модель, которая представляет собой уравнение связи между входными и выходными параметрами. Количество опытов при этом может быть резко сокращено, без значительного снижения точности получаемой модели. Например, для 6-факторного эксперимента на 5 уровнях варьирования факторов, чтобы полностью перебрать все возможные комбинации, требуется провести N = 56 = 15625 опытов, а при соблюдении требований статистики может оказаться достаточным 25. Более подробно получение многофакторных эмпирических зависимостей будет рассматриваться в разделе планирование эксперимента.
Экспериментально-аналитический метод
Этот метод учитывает сильные и слабые стороны аналитического и экспериментального методов. Его сущность заключается в том, что математическая модель составляется аналитическим методом, а ее параметры определяются экспериментально.
Следует отметить, что сразу определить выбор метода обычно не удается и на практике приходится пробовать несколько вариантов.

 .
(2.6)
.
(2.6) (2.8)
(2.8)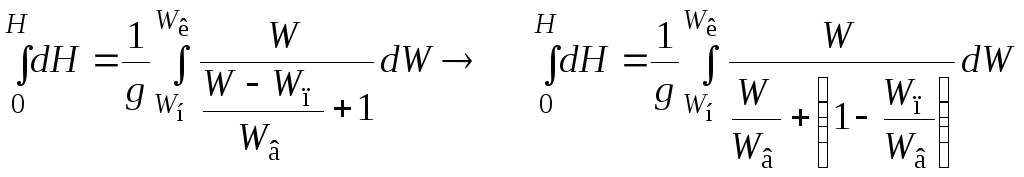 (2.9)
(2.9) , (2.10)
, (2.10) (2.11)
(2.11) .
(2.12)
.
(2.12)