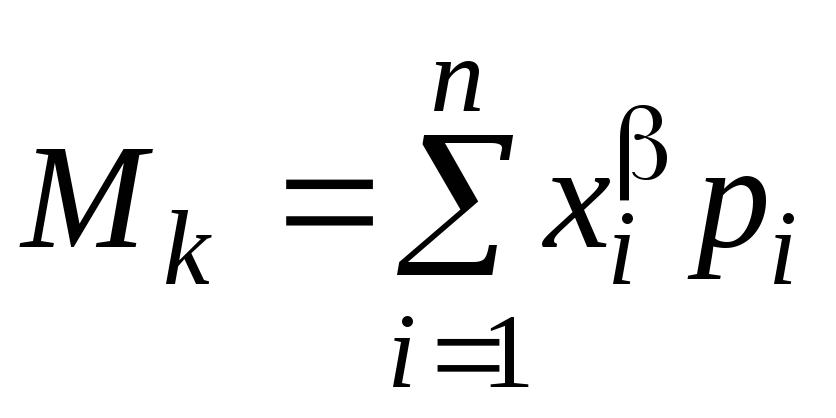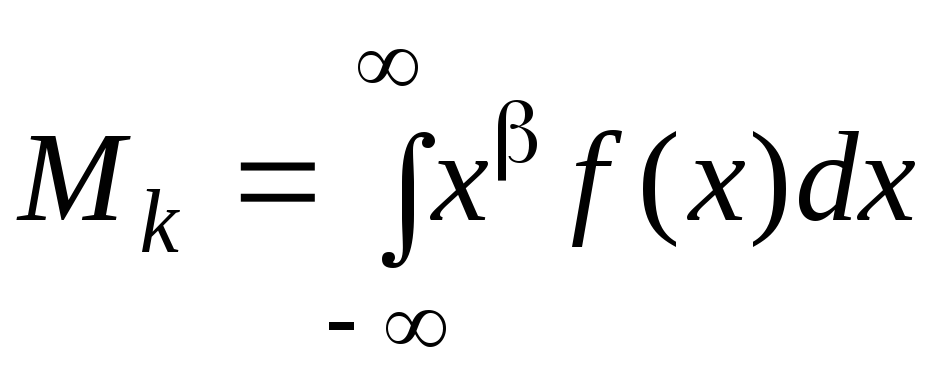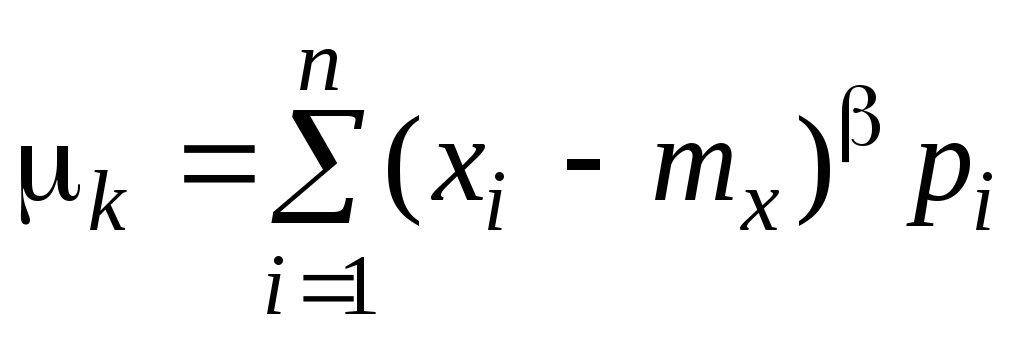4.6. Сравнение аппаратов соответствующих моделям ип и ив

При одинаковых условиях проведения одного и того же процесса аппарат идеального вытеснения эффективнее аппарата идеального перемешивания, так как для достижения равной степени превращения в аппарате идеального перемешивания требуется большее время пребывания потока по сравнению с аппаратом идеального вытеснения. Это объясняется характером распределения концентрации реагентов по объему аппарата. Как известно, скорость протекания процесса пропорциональна его движущей силе, либо величине концентрации взаимодействующих веществ. Для массообменного и химического процесса соответственно

, (4.26)

здесь М – количество переходящего через границу раздела фаз вещества; К – коэффициент массопередачи; F – поверхность контакта фаз; С – движущая сила; k_а – константа скорости реакции; С_а, С_b – концентрация компонентов а и b соответственно.

Так как для аппарата ИВ средняя движущая сила и средняя концентрация компонентов в аппарате будут всегда выше, чем в аппарате ИП, то и время пребывания в нем потока или размеры аппарата потребуются меньшие (рис. 4.11).

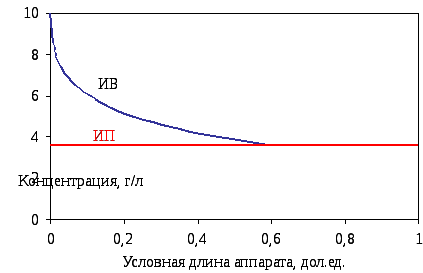
Рис. 4.11. Принципиальный характер изменения концентрации

реагентов по длине аппарата для моделей ИП и ИВ

В научно-технической литературе приводится следующее примерное соотношение средних времен пребывания в аппарате ИП и ИВ, необходимое для достижения равной степени превращения x исходного вещества (рис. 4.12).

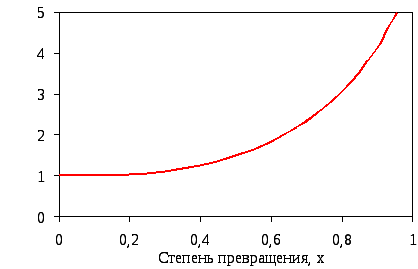
Рис. 4.12. Примерное соотношение среднего времени пребывания в аппарате идеального перемешивания t_ИП и идеального вытеснения t_ИВ

Несмотря на низкую эффективность аппаратов ИП, благодаря простоте их изготовления и эксплуатации они нашли широкое применение в химической промышленности. Для интенсификации процессов в данном случае применяют каскад аппаратов ИП.

5. Методы статистического анализа эксперимента

5.1. Основные характеристики случайных величин

Случайные величины и законы распределения

Под случайной величиной понимают такую величину, значение которой принципиально нельзя предсказать, исходя из условий проведения опыта. Случайная величина обладает целым набором допустимых значений, но в результате каждого отдельного опыта принимает лишь какое-то одно из них. Непредсказуемость значений случайной величины обусловлена наличием случайных факторов, влияние которых на результаты опыта не поддается точной оценке.

Случайные величины бывают дискретные и непрерывные. Возможные значения дискретных случайных величин можно перечислить заранее. Для непрерывных случайных величин реально указать только диапазон их возможных значений. Например, можно точно перечислить количество элементов трубопровода, которые выйдут из строя в течение года (от 0 до n элементов), но нельзя перечислить точные значения скорости их износа или точное время перехода в предельное состояние.

Пусть дискретная случайная величина Х может принимать в результате опыта значения х₁, х₂, ... , х_k. Тогда отношение числа опытов m_i, в которых Х приняла значение х_i, к общему числу проведенных опытов n будет называться частотой появления события Х = х_i. Частота m_i/n также является случайной величиной и меняется в зависимости от количества проведенных опытов. При большом числе опытов она имеет тенденцию стабилизироваться около некоторого значения р_i, называемого вероятностью события Х = х_i, т.е.

при . (5.1)

Вероятность появления случайного события х_i изменяется в пределах от 0 до 1. Сумма вероятностей всех возможных значений случайной величины всегда равна единице,

. (5.2)

Дискретную случайную величину можно задать вероятностным рядом, указав вероятность р_i для каждого значения х_i:

хi	x1	x2	х3	. . .	xn
рi	p1	p2	p3	. . .	pn

Соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения.

Распределение непрерывной случайной величины нельзя задать при помощи вероятностей отдельных значений. Число значений настолько велико, что вероятность появления большинства из них равна нулю. Для непрерывных случайных величин изучается вероятность того, что в результате опыта значение случайной величины попадет в некоторую заранее намеченную совокупность чисел. Если принять, что х произвольное действительное число, а Х случайная величина, то вероятность появления Х < х является функцией от х и называется функцией распределения случайной величины,

Р(Х < х) = F(x). (5.3)

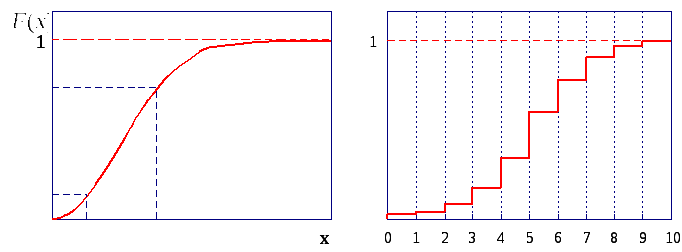
В виде функции распределения можно задать распределение как непрерывной, так и дискретной случайной величины (рис. 5.1, а, б). Ордината кривой F(x₁), соответствующая точке х₁, представляет вероятность того, что случайная величина окажется меньше х₁. Разность ординат, соответствующая точкам х₁ и х₂, дает вероятность того, что значения случайной величины будут лежать в интервале между х₁ и х₂.

Р(х1  Х  х2) = F(x2) – F(x1). (5.4)

Значения функции при предельных значениях аргумента соответственно равны 0 и 1:

F(– ) = 0; F(+ ) = 1. (5.5)

а б

Рис.5.1. Функции распределения непрерывной (а) и дискретной (б) случайных величин

Производная функции распределения называется плотностью распределения случайной величины Х (рис. 5.2). Если F(x) непрерывна и дифференцируема, то

. (5.6)

Рис. 5.2. Плотность распределения

непрерывной случайной величины

Функция f(x) так же, как и F(x), полностью определяет случайную величину. Площадь, ограниченная осью х, прямыми х = х₁ и х = х₂, и кривой плотности распределения, равна вероятности того, что случайная величина примет значения из интервала х₁  х₂:

. (5.7)

Полная площадь под кривой плотности распределения определяется как

. (5.8)

Числовые характеристики

В большинстве прикладных задач оперируют не с законами распределения, а с числовыми характеристиками, выражающими характерные особенности случайной величины и называемыми моментами случайной величины. Аналогично моментам функции РВП (см. раздел 3.2) моменты случайной величины бывают двух видов: начальные и центральные.

	Дискретные	Непрерывные
Начальные			(5.9)
Центральные		,

где  = 1, 2, ... – номер момента.

Начальный момент первого порядка М₁ называется математическим ожиданием (средним значением) случайной величины. Математическое ожидание принято обозначать: M[X], m_x, m. Чаще, чем начальные, используют центральные моменты. Первый центральный момент всегда равен нулю ₁ = 0. Второй центральный момент ₂ называется дисперсией. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е.

. (5.10)

Другие принятые обозначения дисперсии: D[X], D_x, _х². Для дискретной и непрерывной случайных величин дисперсия определится следующим образом:

	Дискретные	Непрерывные
	;	.	(5.11)

Корень квадратный дисперсии называется средним квадратичным отклонением или стандартом.

. (5.12)

Моменты более высокого порядка используются реже.

Моменты существуют, если соответствующие интегралы или ряды для дискретных величин сходятся. Для случайных величин, значения которых ограничены, моменты всегда существуют. Если у случайной величины существуют первый и второй моменты, то можно построить нормированную случайную величину:

Х0 = (Х – mх)/х. (5.13)

Для нормированной случайной величины

M[Х0] = 0; D[Х0] = 1. (5.14)

Многие таблицы распределений построены именно для нормированных случайных величин.

Моменты являются общими (интегральными) характеристиками распределения. Вторая группа параметров характеризует отдельные значения функции распределения. К ним относятся квантили (рис. 5.3).

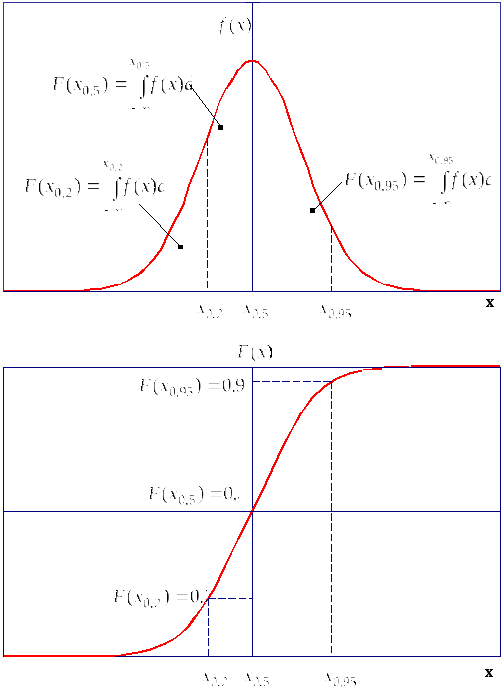
Рис. 5.3. Квантили распределения случайной величины

Квантилем х_р распределения случайной величины Х с функцией распределения F(x) называется решение уравнения

F(xp) = p, (5.15)

т.е. х_р такое значение случайной величины, что

Р(Х < хр) = р. (5.16)

Если известны два квантиля х_р и х_q, то

Р(хр  Х  хq) = q – р. (5.17)

Наиболее важное значение имеет квантиль х_0,5, называемый медианой распределения (см. рис. 5.3). Ордината медианы рассекает кривую вероятности пополам.

Значения квантилей нормального распределения для наиболее используемых вероятностей приведены в табл. 5.1.

Таблица 5. 1

Квантили нормального нормированного распределения

х0,01	х0,05	х0,1	х0,2	х0,5	х0,8	х0,9	х0,95	х0,99
–2,33	–1,64	–1,28	–0,84	0	0,84	1,28	1,64	2,33

Квантили х_р и х_1–р называют симметричными. Для симметричного относительно нуля распределения всегда

хр = –х1–р. (5.18)

Свойства математического ожидания и дисперсии

Математическое ожидание неслучайной величины равно значению этой величины

M[c] = c. (5.19)

Неслучайную величину можно вынести за знак математического ожидания,

M[cX] = c M[X]. (5.20)

Математическое ожидание суммы случайных величин равно сумме математических ожиданий этих случайных величин,

M[X1 + X2 + ... + Xn] = M[X1] + M[X2] + ... + M[Xn]. (5.21)

Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий,

M[X1 X2  ... Xn] = M[X1] M[X2] ... M[Xn]. (5.22)

Случайные величины называются независимыми, если каждая из них имеет самостоятельное распределение, не зависящее от возможных значений других величин.

Дисперсия неслучайной величины равна нулю

D[c] = 0. (5.23)

Неслучайную величину можно вынести за знак дисперсии,

D[cX] = c D[X]. (5.24)

Дисперсия случайной величины равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания,

D[X] = M[X2] – mx2. (5.25)

Дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин,

D[X1 + X2 + ... + Xn] = D[X1] + D[X2] + ... + D[Xn]. (5.26)