2.3. Надежность ремонтируемой аппаратуры с простейшим потоком

Расчетные соотношения

(t) – параметр потока отказов (интенсивность потока отказов),

T₀ – средняя наработка между отказами,

p(t) – вероятность безотказной работы после восстановления,

q(t) – вероятность отказа после восстановления,

f(t) – плотность распределения вероятности отказов после восстановления,

, (k – число отказов за промежуток времени от t₀ до t),

,

, в частности, .

Когда интервал времени невелик (число k мало), Т₀ может отличаться от Т_ср. С увеличением интервала времени и числа отказов, произошедших на нем, для стационарного потока значения параметров T₀ и  стремятся к средним значениям:

T₀ = T_ср,  = , .

Задача № 2.3.1

Оценить вероятность отказа одного ремонтируемого изделия в течение некоторой наработки после восстановления, если известно, что для 200 аппаратов с такой наработкой произошло 100 отказов.

Решение

Параметр потока отказов .

Интенсивность отказа одного аппарата .

Вероятность отказа = 0,39347.

Ответ:  40 %.

Задача № 2.3.2

Найти установившееся значение параметра потока отказов, если интенсивность отказов изменяется во времени (t) = at.

Решение

Установившееся значение параметра потока отказов равно интенсивности отказов, только если интенсивность постоянна. В данном случае интенсивность не постоянна, но постоянно значение среднего времени до отказа:

.

Используя соотношения взаимосвязи для установившихся зна- чений,

.

Ответ: .

2.4. Поток с ограниченным последействием

Расчетные соотношения

В потоках с ограниченным последействием зависимость потока отказов от времени можно найти из интегрального уравнения

,

воспользовавшись преобразованием Лапласа

,

где (s) и f(s) – преобразование Лапласа функций (t) и f(t).

Примечание

Прямое и обратное преобразование Лапласа

,

, s =  + i.

Т а б л и ц а 4.1
Оригинал x(t)	Образ X(s)
a	a/s
at	a/s2
at2	2a/s3
atb	b!a/sb+1, b > 0
ae–t	a/(s+)

Для нахождения образа функции и оригинала по образу (прямое и обратное преобразование) используются таблицы соответствия (табл. 4.1).

Свойства преобразования:

1) линейность X(s) = aX₁(s) + bX₂(s)

 x(t) = ax₁(t) + bx₂(t);

2) дифференцирование оригинала

L{дx/дt} = sX(s) – x(0),

L{д²x/дt²} = s²X(s) – sx(0) – x´(0);

3) интегрирование оригинала

.

Задача № 2.4.1

При изготовлении и ремонте аппарата предприятием используются конденсаторы двух поставщиков: 40 % с интенсивностью отказов ₁=610^–6 1/ч и 60 % с интенсивностью ₂=10^–6 1/ч. Определить интенсивность параметра потока отказов.

Решение

Плотности распределения вероятностей отказов конденсаторов:

и .

Поскольку полная вероятность есть сумма произведений условных вероятностей появления события (отказ конденсатора) на вероятность гипотезы (использовался конденсатор первого или второго поставщика), результирующая плотность распределения вероятности отказа вычисляется как суперпозиция исходных распределений:

,

где с₁ + с₂ = 1 – весовые коэффициенты, в нашем случае c₁=0,4; c₂=0,6.

Поскольку закон распределения не является экспоненциальным, параметр потока отказов не будет постоянным во времени, и поток будет иметь последействие. Чтобы вычислить параметр потока отказов, найдем преобразование Лапласа от плотности распределения:

.

Преобразование Лапласа от параметра потока отказов:

,

.

Обозначим ₀ = c₁₁+c₂₂, ₃ = ₁c₂+₂c₁.

Тогда .

С помощью обратного преобразования Лапласа находим оригинал:

.

Подставляя значения, получаем:

₀ = 310^–6, ₃ = 410^–6,

=1,510^–6, =1,510^–6,

(t) = 1,510^–6 + 1,510^–6 exp(–410^–6t).

Зависимость параметра потока отказов от времени представлена на графике (рис. 4.1).

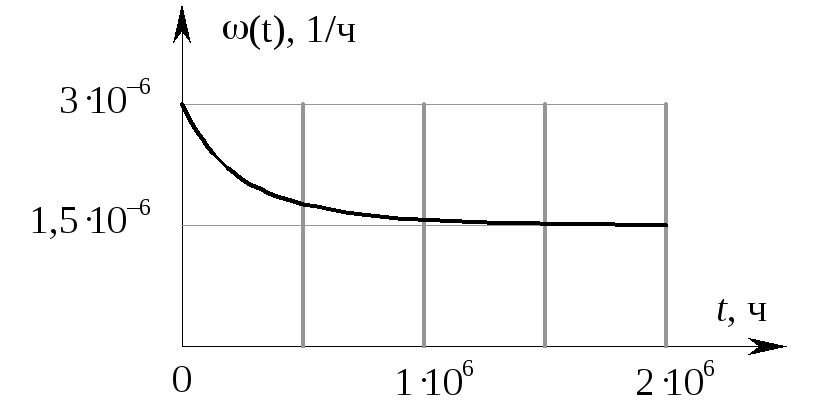
Рис. 4.1

Задача № 2.4.2

У деталей, используемых для изготовления и ремонта аппаратов, интенсивность отказов в выключенном состоянии ₁=10010^–6 1/ч, во включенном состоянии ₂=10^–6 1/ч. Определить интенсивность параметра потока отказов.

Решение

Поскольку вероятность отказа в выключенном состоянии существует, суммарная наработка до отказа будет складываться из среднего времени пребывания в выключенном состоянии и среднего времени работы:

T = T₁ + T₂.

Таким образом, суммарная наработка есть случайная величина, являющаяся суммой двух независимых случайных величин с плотнос-тями распределения вероятностей:

и .

Согласно теории вероятностей плотность распределения суммы двух независимых случайных величин есть композиция (свертка) их плотностей распределения:

.

Преобразование Лапласа для этого выражения:

f(s) = f₁(s) + f₂(s),

где ,.

Откуда .

Находим преобразование Лапласа параметра потока отказов

.

С помощью обратного преобразования Лапласа находим оригинал:

.

Подставляя значения, получаем

(t) = 0,9910^–6 (1 – e^{–0,000101 t} ).

Зависимость параметра потока отказов от времени представлена на графике (рис. 4.2)

Рис. 4.2