Teoriya avtomatichnogo keruvannya

проектування САК, який з часом було вдосконалено і розвинуто іншими вченими. Цей метод дістав назву методу змінних стану.

Метод змінних стану дає можливість визначити залежність вихідних (керованих) параметрів багатовимірної системи х,, х 2 , х г (в узагальненому вигляді х) від деяких змінних стану у{,...9уп (в узагальненому вигляді у) з урахуванням дії керуючих впливів щ ,..., ит (в узагальненому вигляді и).

Отже, в узагальненому спрощеному вигляді рівняння стану можна записати так:

де А, В, С — відповідно матриці стану, керування, виходу (вихідних координат).

Розглянемо принципові загальні положення даного напряму теорії автоматичного керування.

Для описання динамічних процесів у системі автоматичного керування необхідно в загальному випадку встановити характер зміни в часовому просторі керованої величини х системи з параметрами Ь{,...,Ьп від збурень / , , . . . , / „ (до складу збурень належать

задавальні і керуючі функції и(і)).

Поширення дістав спосіб описання систем, що базується на диференціальних рівняннях і передаточних функціях, які застосовують

водновимірних системах.

Убагатовимірній системі з п змінними хх,..., хп при дії в загальному випадку збурень / , , . . . , /п для описання системи необхідно мати систему п рівнянь вигляду

де с!ік (/;) — поліном від оператора р = — .

160

3.14.Багатовимірні системи та метод змінних стану

Уразі застосування перетворення Лапласа при ненульових початкових умовах ці поліноми є функцією деякої комплексної величини

5 і мали б записуватись у вигляді с1ік(з). При нульових початкових умовах, як зазначалося раніше, поліноми можна записувати у вигля-

ді СІік (р).

Перехід від рівнянь ланок конкретної системи і визначення системи рівнянь та їх коефіцієнтів вигляду сІік(р) для описання конкретної САК досить детально викладено раніше на конкретному прикладі застосування теореми Крамера.

У разі багатовимірних систем їх описання і дослідження значно ускладнюються. Тому для дослідження таких систем розроблено так званий метод змінних стану, який може застосовуватись також і для

Ці початкові умови визначать подальший рух системи.

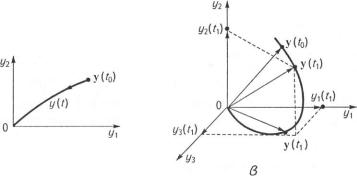
Для характеристики внутрішнього стану системи вводять деякі абстрактні характеристики системи у{ (і), у2(і),..., уп(і)з початковими умовами ух (0), ^(О),..., >>„(0), за допомогою яких з урахуванням вхідної дії и(/) можна однозначно визначити динамічні процеси в системі.

Змінні ух (і),..., уп(і) називають змінними стану системи.

У загальному вигляді деяка змінна стану ук (і) записується так:

УА0 = ЛІУі (0)... у„(0); щ (і)... ит№

Стан системи в довільний момент часу і визначають за допомогою вектора стану у(/), що є функцією змінних стануук (і)(к = 1 ,...,п):

Множину всіх значень вектора стану у (і) на деякому інтервалі

зміни часу і називають простором стану або фазовим простором. Й о -

го можна розглядати як деякий ^-вимірний абстрактний простір, що відповідає порядку диференціального рівняння системи.

Кінець вектора стану при русі в просторі стану має множину по-

л о ж е н ь , я к а називається траєкторією вектора стану або фазовою

траєкторією. Кожна фіксована точка цього положення називається

зображуючою точкою.

Фазовий простір, який відповідає рівнянню динаміки першого порядку, називають одновимірним. Його можна зобразити як пряму на деякій площині, а фазову траєкторію — як сукупність точок (відрізок) на цій прямій.

При п = 2 вектор стану є функцією двох змінних ух (і) і у2(і). Фазовий простір при цьому називають двовимірним. Він є площиною з координатами ух - у2, а фазова траєкторія — крива на цій площині.

Тривимірний простір відповідає системам при п= 3.

Фазові траєкторії і простори стану одно-, дво- і тривимірних систем зображено на рис. 3.41, а—в.

Рис. 3.41

При п - 4 матимемо чотиривимірний простір і т. д.

При застосуванні методу змінних стану виділяють поняття просто-

ру керувань, простору виходів і простору збурень. При цьому під прос-

тором керувань розуміють множину можливих значень их (і), и2(і),...

т=[мо,мо,...,/,(()]'.

162

3.14. Багатовимірні системи та метод змінних стану

Фізична суть змінних стану (які, як було вказано раніше, в загальному випадку можуть бути абстрактними величинами) залежить ні і вибору базису, при зміні якого можна змінити і змінні стану.

ІІрп дослідженні конкретних систем за змінні стану приймають •и'які фізичні величини, які характеризують поведінку даної системи.

Рівняння стану. Якщо вважати, що похідна сіуі (і)/сіі = г, залежить тільки від поточного стану системи, то систему автоматичного керування можна описати системою диференціальних рівнянь першого порядку в нормальній формі Коші, згідно з якими похідні змінних стану залежать від значення змінних, часу і керу-

пані. //,(/).

Знаючи змінні стану, знаходимо кожний з вихідних сигналів хДг)

Якщо рівняння (3.103), (3.104) вважати лінійними (лінеаризовапимп), а систему детермінованою, то ці рівняння однозначно визначають поведінку системи. Ці рівняння називають рівняннями стану І истеми. При зазначених вище умовах змінні стану і вихідні величини не залежать від моменту появи вхідного сигналу щ(і).

І Іри цьому рівняння (3.103), (3.104) можна записати у вигляді

163

хг(() = сГІу1 (() + сг2у2(0 + ... + сгпу„(() +

+(0 + </г2 «2 (0 + • • • + <*тин(і),

де аік,Ьік,сік,(1ік — сталі коефіцієнти, знайдені при визначенні і перетворенні відповідних функцій ф, , у, в рівняннях (3.103), (3.104).

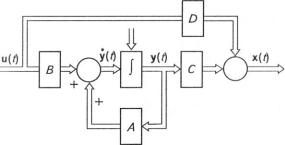
Для складних об'єктів запис рівнянь вигляду (3.105), (3.106) та їх перетворення при дослідженнях системи утруднені, тому значне поширення дістала раціональніша компактна векторно-матрична форма рівнянь стану. Згідно з цією формою рівняння стану можна записати у вигляді

У = Ау(П+ В и(/);

де

(3.108)

є матриця стану розмірністю пхп, яка визначає вільні і вимушені рухи системи;

Ь„,Ь „-,...Ь,

164

3 . 1 4 . Багатовимірні системи та метод змінних стану

•\ит\рицн керування (матриця входу) розмірності пхт, яка визначає

п»а< ми іанежпість входу системи і змінних стану;

сгХ\сх г2"

- і ш три ця вихідних координат (матриця виходу) розмірності г х п, яка ми шачає характер взаємозв'язку вихідних величин зі змінними ста-

ну,

> маїриця розмірністю г х /7, що характеризує прямии зв язок вихіднії координат х/ (і) з керуванням; визначає безпосередній вплив керн мані ія на різні складові вихідних координат; для багатьох систем

Рис. 3.42

Знаходження рівнянь стану і аналогових моделей сис-

тем Розглянемо одновимірну систему, динаміка якої описана дифе- і" шпачинім рівнянням А/-ГО порядку, зведеним до нормованого ви-

165

гляду, при якому коефіцієнт за найвищого порядку похідної від регульованої величини х дорівнює одиниці (о0 = 1); и(()— вхідна величина. Отже, вихідне рівняння має вигляд

На основі рівнянь (3.113) і (3.1 14) можна дістати систему диференціальних рівнянь першого порядку:

Звідси знаходимо систему рівнянь стану (3.115) в матричній формі:

166

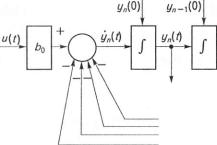
Схему аналогового моделювання одновимірної системи автомаиі'шого керування, що відповідає рівнянням (3.115), наведено на риє. 3.43. У модель введено початкові умови змінних стану »•„(()),..., ух (0), а також значення коефіцієнтів ах,...,ап. Змінюючи ичідну величину и(і) за допомогою даної аналогової моделі, можна аістати залежність х(і).

Загальна методика розв'язання рівнянь стану. Однорічні рівняння. Однорідне рівняння стану (яке не враховує дію вхідних величин и(/)) є векторно-матричним рівнянням вигляду

1 6 7

Рис. 3.43

Воно визначає вільні коливання системи. Позначимо початкові умови: у, (0), >>2(0),... >>„(()). їхній вектор

Відповідне скалярне диференціальне однорідне рівняння

Зінтегрувавши обидві частини останнього виразу, дістанемо

Розклавши експоненціальну(Т)=е"'функці( 0)ю. е"' в степеневий ряд, одержимо

Для матричної функції е згідно з формулами матричного числення маємо

168

3.14. Багатовимірні системи та метод змінних стану

1 Іідставляючи в ліву частину виразу ( 3 . 1 2 5 ) відповідне значення з ( І. І 23), а в праву — з ( 3 . 1 2 4 ) , бачимо, що вони тотожні, а це дає змогу сіверджувати, що ( 3 . 1 2 4 ) — загальний розв'язок векторно-матрично- и> рівняння.

Основні властивості перехідної матриці стану наведено без відпоиі.'цшх доказів.

1. Вимірність перехідної матриці стану дорівнює вимірності динамічної квадратної матриці А. Тому вона також є квадратною матрице ю розмірності п х п, а її складові — функціями часу.

2. При і = 0

=1.

Перехідна матриця стану еАг є неособливою матрицею, а це можливо при умові, що сіег еАі Ф 0.

4. Для перехідної матриці стану еАіеВї = е(А+ В)г лише тоді, коли

І// ПА.

(). {І еА' =еАГ =еА'А.

169