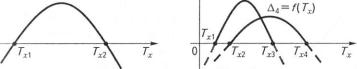Глава 4 |
СТІЙКІСТЬ НЕПЕРЕРВНИХ ЛІНІЙНИХ СИСТЕМ |
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
систему може зробити нестійкою. Згідно з цим вертикальну (уявну)
вісь у комплексній площині конів називають межею стійкості.
Відстань до уявної осі найменшого «лівого» кореня (за відсутності «правих» коренів або коренів, які знаходяться на уявній осі) харак-
теризує запас |
стійкості |
системи . |
|
Наявність |
нульового |
коре- |
|
|
|
|
|
|
|
Ре |
УР |
|
|
|
ня |
або |
пари чисто уявних |
X |
|
Р9 |
|
|
Рг |
коренів р9, |
р10 зумовлює особ- |
|
|
|
|
х |
ливий випадок поведінки сис- |
|
|
|
|
|
|
|
Рв |
|
|
|
|
теми — перебування її на межі |
|
|
|
|
|
|
|
|
-X |
а |
|
стійкості. |
|
|
|
|
Р 5 |
Р 4 |
|
р 1 |
|
При |
дослідженні |
рівняння |
|
|
|
|
|
Рз |
|
Рі |
|
Рю |
|
|
першого |
наближення |
виникає |
|
|
|
X |
X |
|
|
|
|
|
принципове |
запитання: |
якою |
|
|
|
|
|
|
мірою |
результати, які |
можна |
|
|
рис ^ ^ |
|
дістати при цьому, відповіда- |
|
|
:—— |
|
тимуть реальним нелінеаризо- |
|
|
|
|
|
|
ваним |
системам? |
|
|
Висновки дослідження цього принципового питання, відомі як |
теореми Ляпунова, |
наведено нижче без доведень. |
|
|
|
|
|
|
|
|
Теорема 1 |
|
|
|
|
|
|
Якщо |
всі |
корені характеристичного |
рівняння |
лінеаризованої систе- |
ми є |
від 'ємними |
або |
комплексними з |
|
від 'ємною |
дійсною частиною, |
то збурений рух вихідної (нелінеаризованої) системи буде стійким |
незалежно |
від |
значення відкинутих |
|
при лінеаризації членів |
ряду |
Тейлора. |
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 2
Якщо серед коренів характеристичного рівняння лінеаризованої системи є додатні корені або комплексні корені з додатною дійсною частиною, то збурений рух вихідної системи буде нестійким незалежно від значення відкинутих при лінеаризації членів ряду Тейлора.
Теорема З
Якщо серед коренів характеристичного рівняння лінеаризованої системи є нульові або чисто уявні, то для оцінки стійкості вихідної системи необхідно враховувати нелінійні складові ряду Тейлора, відкинуті при лінеаризації.
Наведені теореми є теоретичною основою можливої оцінки стійкості реальних (вихідних) систем за допомогою лінеаризованих рівнянь.
4.4.Алгебричні критерії стійкості
( ного часу існували відомі складнощі щодо знаходження коренів алгебраїчних рівнянь високого порядку. Тому було розроблено метопі, що дають змогу досліджувати стійкість САК без знаходження ко- р т і в характеристичного рівняння. Ці методи дістали назву критеріїв
стійкості.
Зараз у зв'язку із поширенням комп'ютерів і застосуванням чистіших прикладних програм труднощів у визначенні коренів практично не існує, проте критерії стійкості не втратили свого значення. Нони дають змогу не тільки визначити факт стійкості або нестійкос- п їх широко застосовують для визначення запасу стійкості, вирішення задач щодо підвищення якості систем та їх корекції, визначення амплітуди і частоти автоколивань нелінійних систем тощо.
Існують два основні види критеріїв стійкості: алгебричні та часіотні.
4.4
Алгебричні критерії стійкості
о алгебричних критеріїв стійкості належать крите- |
Дрії Рауса, Гурвіца, |
Вишнєградського, Льєна- |
ра Шіпара, до частотних — критерій |
Михайлова та його наслідок |
(друге формулювання критерію), критерій Найквіста, метод О-роз- (нптя, логарифмічні критерії.
Алгебричні критерії дають змогу оцінювати стійкість за коефіцієнтами характеристичного рівняння замкнутої системи.
Як вказувалося раніше, характеристичне рівняння одноконтуріюї замкнутої системи
Р(р)+0(р)= о.
Після перемноження співмножників, які входять до складу опе- ,>агорів Р(р) = Рх (р)Р2(р)... РП(Р); <2(Р) = 0, Ші(/>)••• <2„(Р), та зведенігі подібних членів характеристичне рівняння замкнутої системи мамі ме вигляд
а0р"+а{р"-1 + ... + ап_{р+ ап - 0 . |
( 4 . 1 3 ) |
Аналіз перехідних характеристик типових ланок першого і друго- ю порядків свідчить, що для рівняння першого і другого порядків необхідною і достатньою умовами є додатне значення коефіцієнтів,
Глава 4 |
СТІЙКІСТЬ НЕПЕРЕРВНИХ ЛІНІЙНИХ СИСТЕМ |
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
що зумовлюється від'ємними знаками дійсних коренів або дійсних частин комплексних коренів.
Для систем вищого порядку (п > 3), крім додатного знака коефіцієнтів характеристичного рівняння замкнутої системи, необхідно, щоб виконувалися й інші умови згідно з відповідними критеріями.
Критерій Рауса—Гурвіца. Англійський математик Е. Раус (1877 р.) і австрійський вчений А. Гурвіц (1895 р.) незалежно один від одного запропонували критерії, на основі яких стало можливим визначити умови стійкості лінійних САР, виходячи зі значень коефіцієнтів характеристичного рівняння.
Е. Раус запропонував критерій у вигляді алгоритму, на основі якого можна скласти таблицю для оцінки стійкості системи. Критерій А. Гурвіца було представлено визначниками, які формуються за відповідними правилами. Кінцеві результати (умови стійкості) в обох критеріях однакові. Тому в ТАК для них часто використовується одна загальна назва — критерій Рауса—Гурвіца. Проте, враховуючи більшу простоту формування визначників, які визначають умови стійкості, на практиці частіше користуються критерієм Гурвіца.
Згідно з цим критерієм умови стійкості формулюються таким чином:
І |
усі |
корені характеристичного |
рівняння а0рп + ... + ап _ ур + оп = 0 матимуть |
І |
від'ємні дійсні частини (або будуть дійсними від'ємними), якщо при додатному |
| |
І |
знаку всіх коефіцієнтів а0, ..., |
ап будуть додатними головний визначник Гурвіца |
І |
Дл |
> 0 і його діагональні мінори Ап _, > 0, . . . , Д2 > 0. |
Наведемо правило знаходження визначника Гурвіца.
1. По головній діагоналі записують коефіцієнти характеристичного рівняння від ах до ап.
2.Місця зверху від діагоналі заповнюють коефіцієнтами з більшим індексом, а знизу — з меншим.
3.За відсутності відповідного коефіцієнта ставлять нуль.
4.Діагональні мінори визначають із головного визначника Гурвіца викреслюванням відповідних стовпців і рядків.
Розглянемо конкретний приклад формулювання умов стійкості для системи п'ятого порядку.
•Приклад 4.1. Знайти головний визначник Гурвіца і його діагональні мінори для замкнутої системи з характеристичним рівнянням
£ / ( ) / / + <7, рА + #2/;3 + <73/У + а4р + сі5 = 0.
4.4.Алгебричні критерії стійкості
Р о з в ' я з а н н я . Головний визначник Гурвіца має вигляд
|
|
|
|
я, |
Дз |
0 |
0 |
|
|
|
|
|
|
До а2 а4 |
0 |
0 |
|
|
|
|
|
|
0 |
<*\ |
|
Дз 0 |
|
(4.14) |
|
|
|
|
0 |
а0 |
|
0 |
|
|
|
|
|
|
0 |
0 |
|
а3 |
|
|
|
а діагональні мінори — |
|
|
|
|
|
|
|
я, |
#3 |
а5 |
0 |
|
|
|
"з |
|
|
|
а0 |
а2 |
а4 |
0 |
дз = |
|
|
д2 = |
|
ао |
а2 а4 |
|
0 |
а, |
а3 |
а5 |
|
|
|
0 |
|
а3 |
|
|
0 |
а0 |
а2 |
а4 |
|
|
|
|
|
|
|
|
|
|
|
|
Умовами стійкості вданому випадку є: а0 |
> 0, я, > 0,..., а5 > 0 і |
Д5 > 0; |
Л4 > 0; Д3 > 0; Д2 > 0. |
|
|
|
|
|
|
|
|
У системі при п = 3 характеристичне рівняння замкнутої системи має вигляд
а0р3 + ахр2 + а2р + д3 = 0,
а головний визначник Гурвіца —
|
|
|
|
а{ |
а3 |
0 |
|
|
|
|
|
|
а0 |
а2 |
0 |
|
|
|
|
|
|
0 |
а{ |
а3 |
|
|
|
Розкриваючи його за елементами останнього стовпця, дістаємо |
|
А3=а з ( - 1 ) |
яч. |
Я* |
а3А2. |
|
а0 |
а: |
|
|
|
|
|
|
|
|
Звідси можна зробити висновок: оскільки я3 > 0, то Д3 може бути |
|
(шіьше за нуль лише тоді, коли Д2 |
> 0. |
|
|
|
Отже, при п- 3 необхідною і достатньою умовою стійкості систе- |
|
ми ( А2 > 0 (звичайно, при а{) |
> 0; ах |
> 0; а2 |
> 0; а3 > 0). |
|
І Іри п = 4 характеристичне рівняння замкнутої системи |
|
а0р* + аЛ р3 + а2р2 + а3р + а4 = 0, |
|
і визначники Гурвіца — |
|
|
а 3 |
0 |
0 |
|
|
|
|
|
<*і |
|
|
|
Д 4 |
= |
|
а2 |
а4 |
0 |
а4 |
Л3 ; |
|
0 |
ах |
|
0 |
|
|
|
|
|
|
|
|
|
0 |
а0 |
|
а, |
|
|
Глава 4 |
СТІЙКІСТЬ НЕПЕРЕРВНИХ ЛІНІЙНИХ СИСТЕМ |
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
0
|
|
|
|
|
а1а2а3 |
а~а4 |
|
|
|
0 |
я, |
а з |
|
|
|
|
|
-а «сі |
• а3(сі1а2 |
- |
а0а3) |
а;аА |
а3 А2 |
а?аА |
|
0"3 |
|
|
|
|
|
|
|
|
|
|
|
а1а2 |
- а{)а3. |
|
|
З цього |
виразу |
випливає, |
що |
А3 |
> 0 можливе лише за умови |
А2 > 0. Крім того, якщо А з > 0 і а4 |
> 0, то А4 |
обов'язково буде більше |
нуля. |
|
|
|
|
|
|
|
|
Отже, для системи четвертого порядку необхідною і достатньою |
умовою СТІЙКОСТІ системи Є А з > 0. |
|
|
|
|
Інакше |
кажучи, для системи з п = 4 достатньо |
визначити лише |
знак визначника А3. Якщо А3 > 0, то в цьому разі обов'язково виконуватимуться необхідні за критерієм Гурвіца умови А2 > 0 і А4 >0.
Критерій |
Гурвіца здебільшого використовується для систем з |
п < 4. При п > 4 обчислення стають дуже громіздкими. |
|
Критерій стійкості Льєнара—Шіпара. Цей критерій |
розроблено в |
1914 р. і розраховано для систем з відносно великим |
степенем характеристичного рівняння (п > 5). Він по суті є варіацією критерію Гурвіца. Доведено, що за умови сі0 > 0, сі{ > 0,..., ап > 0 при додатному значенні всіх визначників Гурвіца з індексами 3, 5, ... будуть додатними також усі визначники з індексами 2, 4, 6, ... Отже, при А з >0, А5 >0, ... визначники Д2, Д4, Д6, ... обов'язково будуть додатними. Тому при /7 = 5 необхідне виконання умов Д2 > 0, Д4 > 0, а при п= 6 — умов Д5 > 0, А3 > 0.
Умовою знаходження системи на межі стійкості є рівність нулю відповідного визначника.
Загальна методика дослідження впливу параметрів системи на її стійкість за допомогою критеріїв Гурвіца та Льєна- ра—Шіпара. Дослідження впливу деякого параметра Тх на стійкість системи можна проводити в такій послідовності.
1. Згідно з викладеним, відповідно до степеня характеристичного
рівняння |
прийняти умови: |
при п = З А2 |
> 0; при // = 4 Д3 > 0; при /7 = 5 Д4 > 0, Д2 > 0; при |
/2=6 Д5 |
> 0, Д3 |
> 0. |
|
|
1 8 4 |
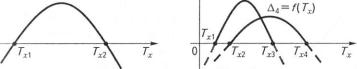
4.4.Алгебричні критері'і стійкості
2Встановити функціональну залежність відповідного визначни-
Іі аію визначників (згідно з п. 1) і параметра Тх:
АХ=/(ТХ).
І Іаприклад, при п = 5 такими залежностями мають бути: /с/;) І А2 = /(Тх).
] умов Дл. = /(Тх) = 0 визначити критичні значення Тх (значенії і І\, за яких система знаходиться на межі стійкості), а також зони, в чі,п\ /\ відповідає стійкому або нестійкому стану системи.
4.У зоні «стійких значень» Тх встановити необхідний запас стій-
іос гі за параметром Тх і виділити зону рекомендованих значень цьо- ю параметра.
Знайдені значення параметра Тх за умовами стійкості надалі трепа узгоджувати з вимогами якості перехідного процесу. Якщо парами ір /\ входить до складу коефіцієнта ап характеристичного рівняним і визначає статичну точність системи, то вимоги стійкості й якості мають узгоджуватися з вимогами статичної точності.
Для ілюстрації викладеної методики розглянемо рис. 4.4. Деяку 11 іежність А3 = /(Тх), що відповідає системі четвертого порядку, умовою стійкості якої є А3 > 0, зображено на рис. 4.4, а. Критичні міачепня параметрів Тх] і Тх2 відповідають А3 = 0, і рекомендоване иіачення параметра Тх має перебувати в межах Тх1—Тх2.
Випадок, що відповідає системі п'ятого порядку (п = 5), наведено па рис. 4.4, б. У цьому разі умовою стійкості є А2 > 0, А4 > 0. Тому
|
|
|
иї ї из виконується із |
врахуванням взаємного розміщення кривих |
Л |
/(Тх)і А4 = /(Тх). У цьому випадку параметр Тх має знаходитися |
н межах Тх2—Тх3, де Тх2 |
і Тх3 — критичні значення параметра Тх. |
А
А2 = Ґ(Тх)
0
\ \
Рис. 4.4
Глава 4 |
СТІЙКІСТЬ НЕПЕРЕРВНИХ ЛІНІИНИХ СИСТЕМ |
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
Критерій ВииінєградсьИого. Цей критерій розроблено в 1877 р. для систем автоматичного керування парових машин, які мали третій порядок рівнянь динаміки, чим обмежується область його використання. І. О. Вишнєградський звів характеристичне рівняння
а0р2 + ахр2 + а2р + а3 = 0,
яке має чотири коефіцієнти, до рівняння з двома коефіцієнтами X, У, які дістали назву параметрів Вишнєградського. Для цього вихідне характеристичне рівняння спочатку було зведено до вигляду
|
а,, |
|
|
|
р3 |
+ |
С | р2 |
+С2р+С3 |
0, |
(4.15) |
де С, |
|
|
|
г - |
|
|
|
|
|
|
= — ; С2 |
|
|
> ^3 ~ |
и п |
|
|
|
|
|
'І |
0 > |
2 ~ |
Оп«о |
|
|
|
|
|
|
а:/а |
|
|
до |
|
|
|
|
|
і для нього знайдено умови стійкості |
|
|
|
|
|
|
|
|
|
|
|
С3 > 0. |
|
(4.16) |
Параметри Хі |
У було запропоновано у вигляді |
|
|
|
|
|
|
X |
|
|
у _ |
С 2 |
|
(4.17) |
|
|
|
|
|
|
|
|
|
|
звідки |
знайдено |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с, |
= |
х ^ - |
с2 |
= |
УіЩ. |
|
Після підстановки значень С, і С2 у вираз (4.16) дістанемо
Х ^ У І І С Ї - с3 > о,
|
або |
ХГ - 1 > 0, |
|
|
або |
|
|
|
|
(4.18) |
|
|
XV > |
1. |
|
|
Останній вираз і є умовою стій- |
|
кості (критерієм) |
Вишнєградського. |
|
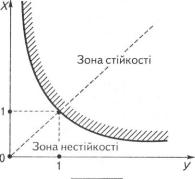
Рівняння межі стійкості в площині |
|
параметрів X, У має вигляд гіпербо- |
|
ли |
(рис. 4.5): |
|
|
|
|
ХУ = |
1, |
(4.19) |
Рис. 4.5. |
я к у |
н а з и в а ю т ь гіперболою |
Вишнє- |
градського. |
|
|
|
|
|
4.4.Алгебричні критерії стійкості
ІІраворуч від кривої міститься зона стійкості ХУ > 1, а ліворуч —
иII і.і нестійких режимів ХУ < 1.
11-і основі наведених формул можна дістати залежності між іншими параметрами, що входять до складу коефіцієнтів а0,... ,а3, і, отже, м нениному вигляді — в рівняння (4.18), (4.19). При цьому залежності п і іншими параметрами, як правило, відрізняються від гіперболіч- п о і о закону.
Приклад дослідження стійкості конкретних систем за ииппмогою алгебричних критеріїв стійкості. Дослідження проведемо ПІЯ конкретної системи стабілізації напруги генератора постійного « іруму, рівняння якої було знайдено в гл. З, а принципову і струкіурпу схеми зображено на рис. 3.28 і 3.29.
Характеристичне рівняння системи стабілізації
|
|
|
ТгТлР3 +(ТГ |
+Тй)р2 |
+ р + кр |
= 0, |
(4.20) |
и' коефіцієнт передачі (підсилення) розімкнутої системи |
|
|
|
|
кр |
= кгкшкКекК, |
|
|
А, |
А'ем, кКе = 1/сд, кк — коефіцієнти відповідно передачі |
генерато- |
рі |
електромагніту, демпфера, резистора; сд — стала демпфера, яка |
і а лежить |
від |
характеристик |
масла і конфігурації поршня самого |
іемпфера |
(наприклад, від числа отворів у |
ньому та їхніх розмірів); |
|
/-з//?з — стала часу генератора постійного струму; Ь3, К3 — |
іп/іуктивність |
і активний |
опір |
обмотки |
збудження генератора; |
/ |
т/сд |
— стала часу масляного демпфера; т — приведена маса ру- |
чомпх елементів системи якоря електромагніту, поршня демпфера, пружини, повзунка реостата.
Розглянемо методику дослідження основних питань стійкості за іопомогою різних критеріїв стійкості для конкретних значень параметрів.
иПриклад 4.2. Нехай Тх = 0,01 с; ТЛ = 0,03 с; кр = 300. Треба дослідити стійкість системи.
Р о з в ' я з а |
н н я . За рівнянням |
( 4 . 2 0 ) |
сформуємо головний визнач- |
ник Гурвіца |
в загальному вигляді: |
|
|
|
т, + |
|
кр |
о |
|
ТГТЛ |
1 |
о |
|
о |
т: + т |
к |
Глава 4 |
СТІЙКІСТЬ НЕПЕРЕРВНИХ л і н і и н и х СИСТЕМ |
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
Для системи третього порядку, крім додатного знака коефіцієнтів, як зазначалося раніше, умовою стійкості є Д2 > 0. Тому в даному разі умову стійкості можна записати так:
Тг + Тп |
кп = тг + т |
•ТгТакр >0~. |
( 4 . 2 1 ) |
Т.Т |
1 |
|
|
Підставивши числові значення параметрів, дістанемо
Д2 = 0 , 0 1 + 0 , 0 3 - 0 , 0 1 • 0 , 0 3 • 3 0 0 = 0 , 0 4 - 0 , 0 9 = - 0 , 0 5 < 0,
що вказує на нестійкість системи.
Аналізуючи умову стійкості Д2 > 0, бачимо, що в теоретичному плані стійкість даної системи можна досягти за рахунок:
•зменшення сталих часу Тг, ТА або однієї з них (тут треба враховувати, що добуток цих параметрів зменшуватиметься більшою мірою, ніж їхня сума);
•зменшення коефіцієнта передачі розімкнутої системи шляхом
зменшення будь-якого коефіцієнта (або коефіцієнтів) передачі, що входять до складу /ср як співмножники;
•одночасної зміни в потрібному напрямку сталих часу і коефіцієнтів передачі.
Вибираючи варіант настроювання системи, насамперед слід враховувати ефективність і технічну зручність вибору і зміни регулюючого параметра системи. З принципової схеми САК і знайдених раніше рівнянь ланок випливає, що з технічної і теоретичної точок зору в даному разі найзручнішим буде зменшення коефіцієнта підсилення (передачі) розімкнутої системи і сталої часу демпфера за рахунок збільшення величини сд. Так, зменшуючи кількість діючих («активних») отворів у площині поршня демпфера, можна збільшити величину сд і зменшити сталу демпфера Тп = т/сІХ. У разі збільшення сд в потрібному напрямку змінюватиметься (зменшуватиметься) також і коефіцієнт підсилення відповідної ланки /сд = 1/сд, а також величина коефіцієнта підсилення розімкнутої системи кр.
Нехай параметр сд збільшимо втричі. Знайдемо нові значення відповідних параметрів системи
= = Та /3 = 0,03/3 = 0,01с;
З С Д
к'р = кр /3 = 300/3 = 100; Т, = 0,01 с.
4.4.Алгебричні критерії стійкості
ІІри ньому
А2 = тГ + г; - тГт;к; = о,о і + о,о і - о,о і • о,о і • іоо =
=0,02 - 0,01 = 0,01 >0.
<ік гема в даному разі є стійкою.
11 Приклад 4.3. Знайти критичне значення параметра /ср, якщо поклас-
шТу = Тй = 0,01 с = сопзі.
Ро з в ' я з а н н я . Критичне значення параметра можна дістати за
умови, що система перебуває на межі стійкості Д2 = 0. І Іри цьому
(* > = |
= М і ± М ! = 200. |
ТтТа |
0,01-0,01 |
І Іри кр > 200 система стає нестійкою.
Цей результат підтверджує сформульоване раніше положення про протилежність вимог динаміки та статики.
Дійсно, чим більше коефіцієнт підсилення наближатиметься до « пою критичного значення, тим менший запас стійкості (зСІ )за даним параметром матиме система:
Зет - ( ^ р )кр ~ ^ р -
Гак, при ТГ = Гд = соп8( і кр = 100 запас стійкості за параметром є гановить
зст = 2 0 0 - 100 = 100. Водночас статична помилка системи
А,
1 + кр
опишіться майже втричі.
Приклад аналізу стійкості за допомогою критерію Пишнєградського. Визначимо, виходячи із умов знаходження системи на межі стійкості, критичне значення параметра/ср для САК напруги імператора, розглянутої раніше.
Дня знаходження параметрів Вишнєградського визначимо коефнік і її її С,, С2 , С3:
1 8 9