
Teoriya avtomatichnogo keruvannya
.pdf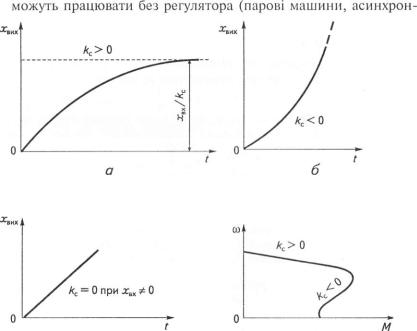
Глава 2 |
основні ЗАВДАННЯ Й ОСОБЛИВОСТІ ТЕОРІЇ |
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
Проаналізуємо |
вираз |
(2.34) |
|
відносно |
коефіцієнта кс. При |
||||||
кс > 0 |
і |
/ - » о о |
хвнх -*хих/кс; |
залежність хвнх |
= / ( / ) |
є |
е к с п о н е н т о ю |
||||
(рис. 2.13, |
а). |
|
|
|
|
|
|
|
|
|
|
Якщо кс < 0 і ^ —> °°, то |
хвих |
-> |
(рис. 2.13, б). |
|
сіхШ1Х = хвх і |
||||||
При |
кс |
= 0 |
рівняння |
динаміки |
матиме |
вигляд |
Та |
||||
^вих = 1 |
г |
|
|
|
|
|
|
|
|
|
сіі |
|
Я к Щ ° *вх |
= сопе* |
, то хвих = (.ха х /Та )ї. У даному разі |
||||||||
* а |
|
|
|
|
|
|
|
|
|
|
|
при і —> оо хвих |
—> °о (рис. 2.13, в). |
|
|
|
|
|
|||||
Отже: |
|
|
|
|
|
|
|
|
|
|
|
•при кс > 0 об'єкти мають стійкий перехідний процес і в принципі можуть працювати без регулятора (електродвигуни та ін.);
• об'єкти з кс < 0 і кс = 0, маючи нестійкі перехідні процеси, не
в |
г |
Рис. 2.13
70
2 . 9 . Рівняння машини-двигуна
~з одним ступенем свободи
ний двигун на нестійкій частині характеристики (рис. 2.13, г) та ін.).
При цьому необхідно зазначити, що автоматичні регулятори, обов'язкові при об'єктах з кс = 0 і кс <0, застосовуються і для об'єк- і і в з /сс > 0. Принципова різниця полягає лише в тому, що при кс > 0 автоматичний регулятор (як буде показано далі) використовується не для досягнення стійкості, а для підвищення якості динамічних режимів (швидкодії, точності).
2.9
Рівняння |
машини-двигуна |
з одним |
ступенем свободи |
Усучасній теорії електропривода досить часто нескладні робочі машини, які є об'єктами в системах автоматичного керування, розглядають разом з приводним дви-
гуном як одне ціле. З цією метою момент інерції (масу) робочої машини приводять до вала двигуна, і далі цей елемент системи робоча машина—двигун вважають по суті об'єктом системи автоматичного керування.
У ряді випадків такий підхід допускається, оскільки при простих робочих машинах кількісне врахування впливу приведеного моменту інерції (маси) може бути достатнім — при цьому не зміниться вигляд математичних залежностей, які відображають динамічні явища в системі керування. Для складних робочих машин, коли необхідно враховувати наявність пружностей в елементах машини, багатомасовість, наявність кількох регульованих параметрів, такий спрощений підхід може виявитися недостатнім.
Якщо вважати зв'язок робочої машини з двигуном абсолютно жорстким, то рівняння динаміки системи робоча машина—двигун матиме вигляд
= |
(2.35) |
де ./ — момент інерції, приведений до вала двигуна; со — швидкість обертання двигуна; Мл — рушійний момент двигуна; Моп — момент опору.
71

Глава 2 |
ОСНОВНІ ЗАВДАННЯ Й ОСОБЛИВОСТІ ТЕОРІЇ |
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
Рушійний момент, як правило, є функцією підведеної ДО НЬОГО енергії, яку відобразимо через положення х відповідного органу регулювання (наприклад, органу регулювання електричної напруги, що подається до електродвигуна, або органу подання пари в парову турбіну), а також швидкості руху со.
Момент опору залежить від швидкості та має деяку незалежну від неї складову /(/).
Згідно з викладеним, рівняння |
(2.35) матиме такий вигляд: |
|
У ^ = Мл (со, х) - |
Мш (ш) - /(/). |
(2. 36) |
Функції Л/д(со, х)та Моп (со) можуть бути заданими у вигляді графічних залежностей або аналітично. В загальному випадку вони нелінійні. Функцію /(/) на час регулювання можна прийняти за сталу величину /(/) = /о-
Злінеаризуємо нелінійні залежності, склавши вирази (2.36) для точки со0, х0 на основі розкладу в ряд Тейлора. Тоді, відкидаючи не-
лінійні члени розкладу, дістаємо |
|
|
|
|
|
|||||||||
|
Мд(со,х) = Л/д0 + |
|
|
|
Асо + |
'дМя Ах ; |
|
|||||||
|
|
|
|
|
|
|
|
|
(70) |
|
х = л'о |
4 дх у о) = (оо |
|
|
|
|
|
М 0 І М = М |
+ |
|
V |
|
ДО). |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Зсо )м =0)о |
|
||
Підставляючи |
знайдені |
вирази |
в рівняння (2.36), враховуючи, що |
|||||||||||
со = со0 |
+ Лсо,та нехтуючи для спрощення записами со = со0 |
і х = х0 , ма- |
||||||||||||
ємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
. |
- |
|
|
|
- |
|
|
до, |
+ |
- |
- / , . |
||
Виключимо рівняння статики Мд{) = Моп{) |
+ / 0 , тоді |
|
||||||||||||
|
|
|
СІЇ |
[ |
дх ^ |
І |
|
д(і) |
Зсо |
|
||||
Вважаючи х вхідною величиною об'єкта, а Асо — вихідною, одер- |
||||||||||||||
жимо рівняння машини-двигуна у відхиленнях у вигляді |
|
|||||||||||||
|
|
, |
|
|
|
|
|
|
|
О |
|
|
„ч |
|
|
|
г/Асо |
+ |
( д М |
— |
З Л |
Асо = —— Ах. |
|||||||
|
|
У |
|
|
^ |
(2. 37) |
||||||||
|
|
|
с!і |
|
|
І Зсо |
Зсо |
) |
дх |
|
||||
72
2 . 9 . Рівняння машини-двигуна з одним ступенем свободи
Для запису у відносних (безрозмірних) величинах, при базових
значеннях х і со, що дорівнюють номінальним хн |
, |
сон, дістанемо від- |
||||||||
|
|
|
|
|
|
Асо |
. |
|
.. |
Ах . |
посне значення вихідної величини ф = —, а вхідної — |
= —, звідки |
|||||||||
|
|
|
|
|
|
<°н |
|
|
|
* „ |
А(о = фшн, Ах = |ііхн. Підставляючи їх у рівняння (2.37), дістаємо |
||||||||||
|
Т СІЦ) |
|
( дМ0 |
дМ^ |
сонф = |
зм„ |
хнц. |
|
||
|
со „ / — + ! |
Зсо |
|
дх |
|
|
||||
|
сіі |
\ |
Зсо |
|
|
|
||||
Дане рівняння в формі Стодоли матиме вигляд |
|
|||||||||
|
|
|
|
|
|
С0„ |
|
|
|
|
|
/сон |
й/ф |
V |
дш |
Зсо |
ф |
= |
(А, |
|
|
|
|
сіі |
|
дМ, |
|
|||||
|
|
|
|
|
|
|
||||
|
дх |
|
|
|
дх |
|
|
|
|
|
де |
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
м, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗМ^ |
|
|
|
|
|
|
|
|
|
|
дх |
|
|
|
|
|
|
стала часу; |
|
|
|
|
|
|
|
|
|
|
|
|
дЛ/оп |
дМд |
С0и |
|
|
|
|
||
|
|
|
Зсо |
|
Зсо |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2. 38) |
||
|
|
|
|
З^Д |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Зх |
|
|
|
|
|
|
коефіцієнт |
самовирівнювання. |
|
|
|
|
|
||||
Знайдений |
вираз |
|
дає |
змогу, |
виходячи |
з |
особливостей зміни |
|||
моментів двигуна Мя та опору Моп залежно від швидкості со, дійти таких висновків.
1. Якщо момент двигуна зі збільшенням швидкості зменшується,
а момент опору зростає, то з урахуванням того, що д М д- завжди більЗх
і не за нуль, коефіцієнт самовирівнювання кс > 0. Отже, як зазначалося раніше, об'єкт може стійко працювати без автоматичного регулятора.
2. При зменшенні моменту опору зі збільшенням швидкості, якщо момент двигуна зменшується, то можливо, що кс < 0. У цьому разі об'єкт не може стійко працювати без регулятора.
73
Глава 2 |
ОСНОВНІ ЗАВДАННЯ Й ОСОБЛИВОСТІ ТЕОРІЇ |
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
Детальніше фізичні особливості взаємодії робочої машини з приводними електродвигунами залежно від особливостей їхніх механічних характеристик розглядаються в теорії електропривода.
Контрольні запитання та завдання
1.Дайте перелік основних особливостей теорії автоматичного регулювання (ТАР).
2.Назвіть основні умови знаходження системи в статичному стані.
3.Як побудувати результуючі статичні характеристики групи послідовно і паралельно з'єднаних ланок?
4.Побудуйте статичну характеристику ланки зі зворотними зв'язками.
5.Яка залежність точності САК від коефіцієнтів підсилення окремих ланок?
6.У чому полягає протилежність вимог статики і динаміки?
7.Наведіть приклади рівнянь статики і динаміки в різних формах запису.
8.Назвіть методи лінеаризації та вкажіть особливості їх застосування.
9. Як використовується гіпотеза малих відхилень при лінеаризації?
10.Що таке коефіцієнт самовирівнювання і як він впливає на характер перехідних процесів?
11. Як |
коефіцієнт |
самовирівнюван- |
ня |
залежить |
від характеристик |
об'єкта? |
|
|
12.Нарисуйте функціональні схеми багатовимірної зв'язаної і незв'я- заної систем.
13.Визначіть статичну помилку розімкнутої системи.
14.Наведіть вирази статичної помилки розімкнутої системи.
15.Від чого залежить статична помилка комбінованої САК?
16.Як одержати рівняння динаміки системи «машина—двигун»?
Глава 1 МАТЕМАТИЧНЕ ОПИСАННЯ
ЛІНІЙНИХ НЕПЕРЕРВНИХ
°1 СИСТЕМ АВТОМАТИЧНОГО
КЕРУВАННЯ
3.1
Типові |
елементи (ланки) |
|
систем автоматичного |
керування |
|
а |
практиці перехідні |
процеси різних за своїми |
Н еІфізичними принципами дії ланок (елементів) можуть визначатися подібними диференціальними рівняннями динаміки, що дає можливість класифікувати ланки за виглядом рівнянь динаміки. Наприклад, з цієї точки зору, до одного типу ланок можна віднести такі, на перший погляд, різні ланки, як механічна рухома маса та електричне активно-індуктивне коло.
Так, рівняння динаміки для механічної маси з моментом інерції ^
можна записати у вигляді |
|
|
Мтн |
= Л/дв |
- Моп |
або при Моп = кю |
|
|
Групуючи вихідні величини в лівій частині рівняння, а вхідні — в |
||
правій, дістаємо |
|
|
СІОд |
( 3 . 1 ) |
|
Ті |
+ |
|
Рівняння динаміки активно-індуктивного кола з електричним активним опором Я та індуктивністю Ь матиме вигляд
Ь— = и - іЯ, сіі
або
Ь— + іЯ = и. |
( 3 . 2 ) |
сіі |
|
75
Глава З |
МАТЕМАТИЧНЕ ОПИСАННЯ ЛІНІЙНИХ НЕПЕРЕРВНИХ СИСТЕМ |
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
Рівняння (3.1) і (3.2) мають аналогічний вигляд, тому характер зміни струму і та швидкості со в перехідних режимах цих елементів буде аналогічним і за класифікацією, прийнятою в теорії автоматичного керування, ці елементи відносять до одного й того самого типу.
З лівої частини рівняння елемента, в якій представлені вихідна величина та її похідні, видно, як швидко та точно реагує ланка на вхідну величину, що записується в правій частині рівняння.
Наявність похідних у лівій частині рівняння означає, що елемент поступово реагує на вхідну величину, перехідний процес діє певний час, коли є відхилення вихідної величини від заданого рівня.
Якщо похідних у лівій частині рівняння динаміки ланки нема, то це означає, що вона миттєво реагує на вхідну величину.
Похідні можуть бути не тільки в лівій частині рівняння динаміки ланки, а й у правій.
У загальному випадку права частина рівняння динаміки ланки показує, на що реагує ланка і з яким коефіцієнтом передачі (підсилення) вхідна величина з'являється на її виході.
Залежно від вигляду правої частини рівняння ланка може реагувати: на саму вхідну величину; тільки на похідну від вхідної величини; на інтеграл від вхідної величини; на вхідну величину та її похідну; на вхідну величину та інтеграл від неї; на вхідну величину, похідну та інтеграл від неї. Можливі й інші варіанти вигляду правої частини рівняння.
Основними динамічними характеристиками ланок є:
•часова характеристика хІШХ = /(/);
•перехідна функція /?(/) = хшіх (/), яка являє собою реакцію ланки на одиничну ступінчасту вхідну дію хІІХ = !(/);
®функція ваги, що є похідною від перехідної функції
Крім названих характеристик, важливими характеристиками ланок є передаточні функції \¥(р) та різні частотні характеристики (докладніше вони розглядатимуться далі).
Відповідно до рівнянь динаміки розрізняють типові динамічні ланки.
Безінерційна (підсилювальна) ланка. її називають також ідеальною статичною ланкою. Вона має як в динаміці, так і статиці однакове рівняння
76
3.1.Типові елементи (ланки) систем
~ |
автоматичного |
керування |
яке показує, що вхідна величина миттєво, без будь-яких відхилень, надходить на вихід елемента з передаточним коефіцієнтом /с. Прикладом таких елементів можуть бути механічні редуктори, які не мають люфтів, електронні лампи, потенціометри та ін.
Аперіодична ланка першого порядку. Її іноді називають інерційним, релаксаційним або одноємнісним елементом.
Рівняння динаміки такої ланки
сіх |
|
|
|
|
|
у _ вих |
^ ВИХ |
^ в х ' |
(3.3) |
||
сії |
|||||
|
|
|
|
||
або в операторному вигляді |
|
|
|
|
|
(Тр + 1)хШІХ |
= кхах. |
(3.4) |
|||
Розв'язок такого лінійного неоднорідного диференціального рів- |
|||||
няння першого порядку має вигляд |
|
|
|
||
*вих - кхііх(\ |
-І/Т |
(3.5) |
|||
|
|
||||
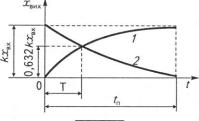
Відповідна часова характеристика |
це експонента (рис. |
З.І, |
|||
крива /). |
|
|
|
|
|
Якщо вхідна величина відсутня |
(що |
відповідає, наприклад, |
від- |
||
ключенню напруги з деякого активно-індуктивного опору), то динамічний процес можна записати у вигляді однорідного рівняння
|
|
|
(Тр + 1)хвих = 0, |
(3.6) |
||
яке називають рівнянням незбуреного руху. Розв'язок його |
|
|||||
|
|
|
х |
= кх |
. |
(3.7) |
|
|
|
НІ,IV |
^^ V ,, V V |
. |
|
|
Відповідна |
часова |
характерис- |
|
|
|
іика зображена на рис. З.І |
(кри- |
|
|
|||
ва |
2). |
|
|
|
|
|
|
В усіх наведених вище рівнян- |
|
|
|||
нях Те стала часу, яка характеризує |
|
|
||||
11 іерційні властивості |
відповідної |
|
|
|||
ланки. |
|
|
|
|
|
|
|
Сталу часу можна знайти за ос- |
|
|
|||
цилограмою |
хвих(ґ). Дійсно, |
при |
Рис. 3.1 |
|
||
/ |
Т з рівняння (3.5) маємо |
|
|
|||
|
|
*вих |
~ кхах (І - е~1) = |
0,632А:хвх. |
(3.8) |
|
77

Глава З |
МАТЕМАТИЧНЕ ОПИСАННЯ ЛІНІЙНИХ НЕПЕРЕРВНИХ СИСТЕМ |
|
АВТОМАТИЧНОГО КЕРУВАННЯ |
Тому для визначення Т достатньо відкласти по вертикальній осі 0,632 хцх і на осі часу і знайти відповідне значення Т.
Тривалість перехідного процесу гп = (3...4)Т. Якщо рівняння динаміки ланки
|
у |
сіх вих |
= |
кх„ |
|
(3.9) |
|
|
сії |
|
|||
|
|
|
|
|
|
|
|
то |
її |
називають |
нестійкою |
аперіодичною |
|
|
ланкою. |
|
|
|
|
|
|
|
Розв'язок цього |
рівняння |
|
||
|
|
|
х вих |
= кхвх V(е'/Т О- |
(3. 10) |
|
|
|
Часова характеристика ланки, |
зображена |
|||
|
на рис. 3.2, показує, що при і —> <*> хаііХ -> <*>. |
|||||
|
|
Аперіодичними ланками є різні електро- |
||||
|
технічні пристрої з активно-індуктивним |
|||||
Рис. 3.2 |
опором, механічні інерційні пристрої, гене- |
|||||
ратори |
постійного струму та ін. |
|
||||
•Приклад 3.1. Вивести рівняння динаміки генератора постійного
струму, принципову схему якого зображено на рис. 3.3, де м>3 — обмотка збудження генератора з індуктивністю Ь і активним опором /?.
Ро з в ' я з а н н я . Якщо прийняти, що швидкість обертання якоря
генератора стала, то напруга генератора иу може змінюватись лише залежно від напруги на обмотці збудження иЛ. В цьому разі рівняння динаміки має дати залежність
=/ ( « , ) .
Для |
обмотки збудження |
|
|
|
|
|
и, |
_ |
# |
сіі, |
Яіг |
иг |
= |
|
Ь^ + |
||
|
|
|
сії |
|
|
|
Виходячи з лінійності характеристики генератора, за- |
||||
|
писуємо |
иГ = сі3, |
|
||
|
иГ |
|
|||
УУ3 |
|
|
|
|
|
звідки /3 = —. |
|
|
|
|
|
і я |
Переносячи вихідні |
|
величини в ліву частину, |
||
и* |
дістаємо |
|
|
Я |
|
Ь сіиГ |
|
|
|||
|
|
= ил |
|||
|
с |
сіі |
+ -иГ |
||
Рис. 3.3 |
|
с |
|
||
|
|
|
|
|
|
78
3.1. Типові елементи (ланки) систем автоматичного керування
Увівши позначення Ь/К = ТГ, с/Я = кГ, матимемо рівняння генератора у вигляді
Т Г ^ + иГ=кГи3, |
(3.11) |
в операторній формі запису |
|
(ТГр+\)иГ =кГи.Л. |
(3.12) |
Ланки другого порядку. До цієї групи належать ланки, рівняння динаміки яких має вигляд
И ~ у |
+ |
/7у |
+ |
=кхт. |
(3.13) |
аі |
|
сіі |
|
|
|
Позначивши 4а -Тх Ь = Т2, дістанемо рівняння в операторній формі запису:
(Т{2р2 +Т2р+ 1)хшіх = кхт. |
( 3 . 1 4 ) |
Розв'язок цього рівняння
* в и х =кхт(С{е*' + С2е* + 1 ) , |
( 3 . 1 5 ) |
де Сь С2 — сталі інтегрування; ри р2 — корені характеристичного рівняння
Т2р2 +Т2р+\ = 0. |
(3.16) |
Залежно від коренів характеристичного рівняння можливі два різновиди ланок другого порядку — аперіодичні та коливальні. Рівняння динаміки цих ланок мають однаковий вигляд, але їхні часові характеристики суттєво відрізняються.
Аперіодичні ланки другого порядку. До ланок цього виду належать лапки при дійсних і від'ємних коренях характеристичного рівняння
|
27] |
|
|
Це можливо за умови, коли |
Т2 > 2Т{. |
|
|
При/?, <0(рЛ = -оі] ),р2<0 |
(р2 |
= -а2)розв'язокрівняння |
ланки |
- ± - + с 2 - 1 |
( 3 . 1 7 ) |
||
е*\г |
2 |
еа2> |
|
79
