Teoriya avtomatichnogo keruvannya

7. ]еАісіх = А~\еАі - І) = (еАі - І)А~\

о

Загальна методика розв'язання неоднорідних рівнянь.

Розглянемо це питання на прикладі стаціонарного векторно-матрич- ного рівняння стану:

у(і) = Ау(і) + Я и(0.

Початкові умови визначаються вектором початкових умов і рівнянням виходу:

х(0=Су(0+Ди(0.

Помноживши на е~Аг обидві частини виразу у(і), дістанемо

е-А'у(і) = е-А'Ау(і) + е-Аі Ви(і),

або

е~Агу(і)~ е~А'Ау(і) = е~АіВхх(і).

Згідно з властивостями матриці маємо

СІІ

тому

?-А'у(і)]=е~А'Ви(і).

аі

Зінтегрувавши обидві частини цього виразу від 0 до Г, матимемо

е-Аіу(і)-у(0) = \е-АхВи(т)сіт.

о

Враховуючи п'яту властивість матриці, дістаємо

у (і) = еА{у(0) + ел']е-АхВх\Шт,

о

або, з урахуванням четвертої властивості,

і

У(/) = е АІу(0) + \см' -т) В и(т)с!х.

0

1 7 0

3.14. Багатовимірні системи та метод змінних стану

ІІерша складова правої частини цього рівняння описує вільні ру-

псистеми, зумовлені початковими умовами, а друга — рух системи, іумовлений вектором керування і реакцією системи з відповідними

нульовими початковими умовами.

Якщо підставити у(/)у вираз х(/), записаний вище, то

Реакція стаціонарної системи не залежить від моменту /0 прикладі ння дії, тому можна записати розв'язок неоднорідного рівняння і іапу у вигляді

111 вирази відповідають розв'язку скалярного рівняння першого порядку

Знайдені згідно з наведеною методикою рівняння стану та їх роз- в'язки можуть бути основою для дослідження поведінки САК у динамічних режимах. Цей процес зводиться до визначення перехідної ї ї і рпці стану еАі. У даному разі це має важливе значення тому, що « і гідові перехідної матриці стану відображують перехідну функцію » псіеми і функцію ваги, які є основними динамічними характерис- і пкамп САК.

Аналіз виразу еАі потребує застосування окремих методів до- » ішжепня. За великих розмірностей п матриці єдиними практично можливими є методи, що базуються на використанні ЕОМ за допо- ю і о і о спеціальних алгоритмів і програм, які наводяться в спеціальній иііературі.

171

Глава СТІЙКІСТЬ НЕПЕРЕРВНИХ 4 ЛІНІЙНИХ СИСТЕМ

АВТОМАТИЧНОГО

КЕРУВАННЯ

4.1

Поняття стійкості САК

Під стійкістю системи в найзагальнішому випадку розуміють її властивість повертатися у початкове (або близьке до того) положення після зникнення дії факторів (збу-

рень), які вивели систему зі стану початкової рівноваги. Стійкість системи є необхідною умовою можливості САК вирішувати поставлені перед нею завдання.

Найпростішим прикладом, що характеризує різні сторони поняття стійкості системи, може бути рис. 4.1.

Розглянемо рух кулі по деякому криволінійному шляху (рис. 4.1, а). Якщо куля переміщуватиметься зовнішніми силами із положення початкової рівноваги 0 в положення І, II або III, то після зникнення цих сил вона повернеться у початкове положення (або близьке до нього) залежно від сил тертя. При цьому можливі коливання кулі відносно початкового положення.

У випадку, що відповідає рис. 4.1, б, куля займає нестійке положення рівноваги 0. Досить незначного зміщення кулі відносно цього положення, і вона не зможе самостійно повернутися до початкового с гану.

Обидва розглянуті варіанти поведінки кулі зображено на рис. 4.1, в. Залежно від початкового положення рівноваги і характеру дії зовнішніх сил у разі відхилень кулі в межах відрізка шляху 0 — І вона повертатиметься у положення 0. У разі виходу за межі цього відрізка повернення в початкове положення стає неможливим.

Для характеристики поведінки кулі в найзагальнішому випадку нелінійних систем використовується поняття стійкості «в малому», и великому» і «в цілому» (для окремих видів нелінійностей її назива-

їо 11. абсолютною стійкістю).

173

Система є стійкою «у великому», якщо визначено межі області можливих відхилень, в яких система повертається у початкове положення, і відомо, що початкові відхилення системи не виходять за межі цієї області. Система стійка «в малому», якщо межі області стійкості не визначені, а вказано лише факт її наявності. Система стійка «в цілому», якщо вона повертається у початкове положення рівноваги за будь-яких початкових відхилень (рис. 4.1, а).

Шлях кулі, зображений на рис. 4.1, в, відповідає стійкості «у великому», якщо початкові відхилення є тільки в межах 0 — І, і нестійкості «у великому», якщо початкові відхилення можливі в межах 0 — II. У цьому випадку система стійка «в малому» (на відрізку 0 — І) і нестійка «у великому» (на відрізку 0 — II).

Система, стійка «в цілому», завади є стійкою «у великому» і «в малому». Система, стійка «у великому», є стійкою «в малому».

В теорії автоматичного керування розрізняють поняття незбуреної рівноваги (положення 0 на рис. 4.1, сі) і збуреного стану, в яке переходить система у разі дії збурення і наступного його зникнення (положення II на рис. 4.1, сі).

Крім відносно простого випадку початкового положення рівноваги, коли об'єкт (куля) нерухомий, можливі й складніші випадки, коли иезбурений стан системи є рухом за деякою траєкторією (наприклад, у програмних САК). Такий стан системи називають незбуреним рухом. У разі дії на систему зовнішніх факторів виникають відхилення від початкового руху, і такий стан системи називають збуреним рухом.

Незбурений рух системи називають стійким, якщо після зняття зовнішніх сил збурений рух через деякий час увійде в задану область є.

При цьому можна записати

де Ах(і)— відхилення координат збуреного руху. 0

Рис. 4.1

174

4.2.Стійкість за Ляпуновим

4.2

Стійкість за Ляпуновим

У 1892 р. О. М. Ляпунов сформулював поняття стійкості, виходячи із того, що незбурений рух є лея ким визначеним рухом системи, що підлягає дослідженню на

і і їй кість. Він міг бути як усталений, так і не усталений. Згідно з цим визначення стійкості за Ляпуновим формулюється таким чином:

незбурений рух є стійким відносно змінних X/, якщо за будь-якого довільно заданого додатного числа є, яким би малим воно не було, можна вибрати друге додатне число 5(є), таке, що за будь-яких збурень х/0, що задовольняють умову

/- 1

ІІрактично стійкість незбуреного руху за Ляпуновим означає, що іа досить малих початкових збурень збурений рух як завгодно мало

відрізнятиметься від незбуреного. Якщо незбурений рух нестійкий, і о збурений все більше відходитиме від нього в разі найменших по- 4 1 гкових збурень.

Основні особливості визначення поняття стійкості за Ляпуновим полягали в тому, що стійкість розглядалася на нескінченному інтервалі часу, збурення були малими і діяли лише на початкові умови. В ГАК існує також поняття асимптотичної стійкості, під яким розуміють таку стійкість незбуреного руху, за якою збурений рух за до-

іиті» малих початкових збурень прагне до незбуреного руху. Теоретично умову асимптотичної стійкості можна записати у ви-

іляді

Іноді умову стійкості технічних систем записують так:

її' А\, (/) — відхилення ординати неусталеного руху відносно відпо-

відної ординати усталеного; е — деяка довільно мала величина.

Унайзагальнішому випадку відповідь на всі питання динаміки < АК, у тому числі стійкості, можна дістати на основі аналізу харак-

175

теристикп перехідного процесу, яку визначають у разі розв'язання диференціального рівняння замкнутої системи.

При виведенні рівняння замкнутої САК, як вказувалось раніше, в багатьох випадках використовується лінеаризація нелінійних залежностей за допомогою ряду Тейлора. Виведене таким чином рівняння називають рівнянням першого наближення.

4.3

розглянемо лінійну САК стабілізації, рівняння ди- р наміки якої в загальному випадку в операторній

формі має вигляд

де /(і) — функція збурення.

Після нескладних перетворень це рівняння можна записати так:

де а0,..., ап, Ь0,..., Ьт — коефіцієнти рівняння, що визначаються параметрами ланок системи (сталими часу та коефіцієнтами передачі); * — регульований параметр.

Наведене рівняння замкнутої системи є неоднорідним лінійним диференціальним рівнянням п-то порядку (п > т). Його розв'язок згідно з відомим принципом суперпозиції

де хпер — перехідна складова, яка є загальним розв'язком однорідного диференціального рівняння

176

4.3.Дослідження і аналіз стійкості

за коренями характеристичного рівняння

яке визначає рух системи після зникнення збурення і називається

рктннням вільного руху; х0 — частковий р о з в ' я з о к неоднорідного рів-

я, який характеризує усталений стан системи (при і = оо), зале- і и гь від параметрів системи та збурення /, але на стійкість системи ік впливає.

Отже, стійкість лінійної системи залежить від розв'язку рівняння ииіьііого руху (4.8)

і' (',,..., Сп — сталі інтегрування, що визначаються з початкових умов; /?,,..., рп — корені характеристичного рівняння, які визначаюіься параметрами ланок системи.

Характеристичне рівняння має вигляд

Отже, можна зробити такі висновки.

1. Стійкість лінійних САК не залежить від величини і вигляду ібуреиь.

2. Стійкість лінійних систем визначається за коренями характеристичного рівняння, які залежать від параметрів системи.

Згідно з викладеним найзагальнішим методом аналізу стійкості є аналіз за коренями характеристичного рівняння.

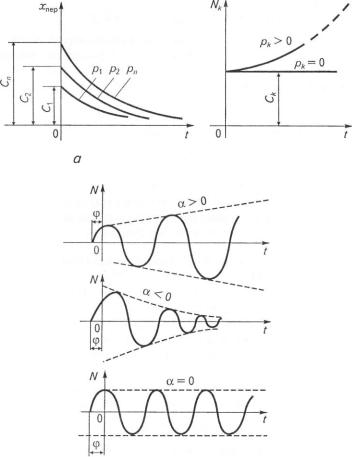
Аналіз стійкості за коренями характеристичного рівняння замкнутої системи. Розглянемо розв'язок рівняння вільного руху залежно від вигляду коренів характеристичного рівняння.

1. Нехай усі корені дійсні та від'ємні: р{ < 0,..., рп < 0. У цьому

І Ігрехідний процес у цьому разі буде затухаючим, а система — стійкою.

її а визначає нестійкість системи в даному випадку (рис. 4.2, б).

І Іехай усі корені характеристичного рівняння дійсні та від'ємні, крім двох:

рк = а + у(3; рк + 1 = а - у(3.

177

Сума складових розв'язку хпер, що відповідає сумі цих коренів, матиме вигляд

+ Ск + Іе|а~уР)' =еа'(СкеЛІ' +Ск + Іе~^').

в

Рис. 42

178

4.3.Дослідження і аналіз стійкості за коренями характеристичного рівняння

Замінивши показникову форму запису на тригонометричну, згідно з формулою Ейлера можна записати

Співмножник £)зіп(рг + ф)є синусоїдою з амплітудою Д зсунуіою відносно початку координат на кут ф. У цьому разі характер іміпп складової N перехідного процесу хпер визначається знаком веіичпни а у співмножнику еш складової N.

нсистемі зі сталою амплітудою В.

4.Якщо всі корені характеристичного рівняння замкнутої систе-

ми дійсні та від'ємні, а один із них рк = 0, то Л^ = Ск буде сталою веінчиною (рис. 4.2, б).

Для зображення поведінки САК залежно від вигляду коренів характеристичного рівняння замкнутої системи часто використовують

іомплексну площину коренів (рис. 4.3).

ІІри цьому корені р{ (дійсний, додатний), р2, р3 (комплексні з доіаіпою дійсною частиною), які знаходяться у правій частині комп-

иі спої площини коренів, розділеній уявною віссю, відповідають не- < мпкіи САК. Ці корені часто називають «правими коренями».

Корені, які знаходяться зліва від уявної вертикальної осі (дійсні, ш м мні /;4, р5, комплексні з від'ємною дійсною частиною рв, р1 —

пні корені»), відповідають стійкій САК.

()тже, перехід коренів з лівої напівплощини в праву у разі зміни и'ікпх параметрів системи, що зумовлює зміну знака коренів, стійку

179